Chapter 1 Integers Exercise 1.4
Question 1.
Evaluate each of the following:
(a) (-30) ÷ 10
(b) 50 ÷ (-5)
(c) (-36) ÷ (-9)
(d) (-49) ÷ (49)
(e) 13 ÷ [(-2) + 1]
(f) 0 ÷ (-12)
(g) (-31) ÷ [(-30) + (-1)]
(h) [(-36) ÷ 12] ÷ 3
(i) [(-6) + 5] ÷ [(-2) + 1]
Solution:

Question 2.
Verify that: a ÷ (b + c) ≠ (a ÷ b) + (a ÷ c) for each of the following values of a, b and c.
(а) a = 12, b = – 4, c = 2
(b) a = (-10), b = 1, c = 1
Solution:

Question 3.
Fill in the blanks:
(a) 369 ÷ ___ = 369
(b) (-75) ÷ ___ = -1
(c) (-206) ÷ ___ =1
(d) -87 ÷ ___ = -87
(e) ___ ÷ 1 = -87
(g) 20 ÷ ___ = -2
Solution:
(a) 369 ÷ ___ = 369 = 369 ÷ 1 = 369
(b) (-75) ÷ ___ = -1 = (-75) ÷ 75 = -1
(c) (-206) ÷ ___ = 1 = (-206) ÷ (-206) = 1
(d) 87 ÷ ___ = 87 = -87 ÷ (-1) = 87
(e) ___ ÷ 1 = -87 = -87 ÷ 1 = -87
(f) ___ ÷ 48 = -1 = (-48) ÷ 48 = -1
(g) 20 + ___ = -2 = 20 ÷ (-10) = -2
(h) ___ + (4) = -3 = (-12) ÷ (4) = -3
Question 4.
Write five pairs of integers (a, b) such that a ÷ b = -3. One such pair is (6, -2) because 6 + (-2) = -3.
Solution:
(a) (24, -8) because 24 ÷ (-8) = -3
(b) (-12, 4) because (-12) ÷ 4 = -3
(c) (15, -5) because 15 ÷ (-5) = -3
(d) (18, -6) because 18 ÷ (-6) = -3
(e) (60, -20) because 60 ÷ (-20) = -3
Question 5.
The temperature at 12 noon was 10°C above zero. If it decreases at the rate of 2°C per hour until midnight, at what time would the temperature be 8°C below zero? What would be the temperature at midnight?
Solution:
Temperature at 12 noon was 10°C above zero i.e. +10°C
Rate of decrease in temperature per hour = 2°C
Number of hours from 12 noon to midnight = 12
∴ Change in temperature in 12 hours
= 12 × (-2°C) = -24°C
∴ Temperature at midnight
= +10°C + (-24°C) = -14°C
Hence, the required temperature at midnight =-14°C
Difference in temperature between + 10°C and -8°C
= +10°C – (-8°C) = +10°C + 8°C = 18°C

∴ Time after 9 hours from 12 noon = 9 pm.
Question 6.
In a class test (+3) marks are given for every correct answer and (-2) marks are given for every incorrect answer and no marks for not attempting any question:
(i) Radhika scored 20 marks. If she has got 12 correct answers, how many questions has she attempted incorrectly?
(ii) Mohini scores -5 marks in this test, though she has got 7 correct answers. How many questions has she attempted incorrectly?
Solution:
Given that:
+3 marks are given for each correct answer. (-2) marks are given for each incorrect answer. Zero marks for not attempted questions.
(i) Marks obtained by Radhika for 12 correct answers = (+3) × 12 = 36
Marks obtained by Radhika for correct answers = 12 × 3 = 36
Total marks obtained by Radhika = 20
∴ Marks obtained by Radhika for incorrect answers = 20 – 36 = -16
Number of incorrect answers

Hence, the required number of incorrect answers = 8
(ii) Marks scored by Mohini = -5
Number of correct answers = 7
∴ Marks obtained by Mohini for 7 correct answers = 7 × (+3) – 21
Marks obtained for incorrect answers
= -5 – 21 = (-26)
∴ Number of incorrect answers
= (-26) ÷ (-2) = 13
Hence, the required number of incorrect answers – 13.
Question 7.
An elevator descends into a nine shaft at the rate of 6 m/min. If the descent starts from 10 m above the ground level, how long will it take to reach -350 m.
Solution:
The present position of the elevator is at 10 in above the ground level.
Distance moved by the elevator below the ground level = 350 m
∴ Total distance moved by the elevator = 350 m + 10 m = 360 m
Rate of descent = 6 m/min.
Total time taken by the elevator
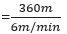
= 60 minutes = 1 hour
Hence, the required time = 1 hour.







