Chapter 11 Perimeter and Area Exercise 11.3

Chapter 11 Perimeter and Area Exercise 11.3

Question 5.
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Solution:
Radius of the circular sheet = 4 cm
∴ Area = πr² = π × 4 × 4 = 16π cm²
Radius of the circle to be removed = 3 cm
∴ Area of sheet removed = πr² = 9π cm²
Area of the remaining sheet
= (16π – 9π) cm2 = 7π cm²
= 7 × 3.14 cm² = 21.98 cm²
Hence, the required area = 21.98 cm².

Question 7.
Find the perimeter of the given figure, which is a semicircle including its diameter.

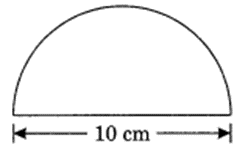
Solution:
Given: Diameter = 10 cm

Hence, the required perimeter
= 25.7 cm. (approx.)

Question 11.
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution:
Side os the square sheet = 6 m
∴ Area of the sheet = (Side)² = (6)² = 36 cm²
Radius of the circle = 2 cm
∴ Area of the circle to be cut out = πr²

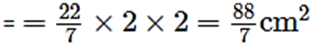
Area of the left over sheet

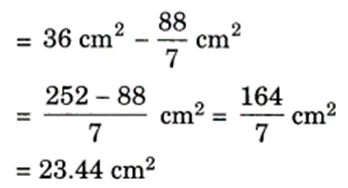
Question 12.
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle. (Take π = 3.14)
Solution:
Circumference of the circle = 31.4 cm
2πr = 31.4

Area of the circle = 7πr² = 3.14 × 5 × 5 = 78.5 cm²
Hence, the required radius = 5 cm and area = 78.5 cm².

Question 14.
A circular flower garden has an area of 314 m². A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler can water the entire garden?
[Take π = 3.14]
Solution:
Area of the flower garden = 314 m²
Radius of the circular portion covered by the sprinkler = 12 m
∴ Area = 7πr² = 3.14 × 12 × 12
= 3.14 × 144 m² = 452.16 m²
Since 452.16 m² > 314 m²
Yes, the sprinkler will water the entire garden.

Question 15.
Find the circumference of the inner and the outer circles, shown in the given figure. (Take π = 3.14)

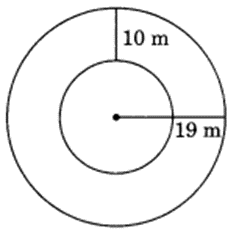
Solution:
Radius of the outer circle = 19 m
∴ Circumference of the outer circle = 2πr
= 2 × 3.14 × 19 = 3.14 × 38 m
= 119.32 m
Radius of the inner circle
= 19m – 10m = 9m
∴ Circumference = 2πr = 2 × 3.14 × 9
= 56.52 m
Here the required circumferences are 56.52 m and 119.32 m.

Question 16.

Question 17.
The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution:
Length of minute hand = 15 cm
∴ Radius = 15 cm
Circumference = 2πr
= 2 × 3.14 × 15 cm = 94.2 cm
Since the minute hand covers the distance in 1 hour equal to the circumference of the circle. Here the required distance covered by the minute hand = 94.2 cm.