Chapter 11 Perimeter and Area

Chapter 11 Perimeter and Area

Very Short Answer Type

Question 1.
The side of a square is 2.5 cm. Find its perimeter and area.
Solution:
Side of the square = 2.5 cm
Perimeter = 4 × Side = 4 × 2.5 = 10 cm
Area = (side)² = (4)² = 16 cm²

Question 2.
If the perimeter of a square is 24 cm. Find its area.
Solution:
Perimeter of the square = 24 cm
Side of the square =  cm = 6 cm
Area of the square = (Side)² = (6)² cm² = 36 cm²

Question 3.
If the length and breadth of a rectangle are 36 cm and 24 cm respectively. Find
(i) Perimeter
(ii) Area of the rectangle.
Solution:
Length = 36 cm, Breadth = 24 cm
(i) Perimeter = 2(l + b) = 2(36 + 24) = 2 × 60 = 120 cm
(ii) Area of the rectangle = l × b = 36 cm × 24 cm = 864 cm²

Question 4.
The perimeter of a rectangular field is 240 m. If its length is 90 m, find:
(i) it’s breadth
(ii) it’s area.
Solution:
(i) Perimeter of the rectangular field = 240 m
2(l + b) = 240 m
l + b = 120 m
90 m + b = 120 m
b = 120 m – 90 m = 30 m
So, the breadth = 30 m.
(ii) Area of the rectangular field = l × b = 90 m × 30 m = 2700 m²
So, the required area = 2700 m²

Question 5.
The length and breadth of a rectangular field are equal to 600 m and 400 m respectively. Find the cost of the grass to be planted in it at the rate of ₹ 2.50 per m².
Solution:
Length = 600 m, Breadth = 400 m
Area of the field = l × b = 600 m × 400 m = 240000 m²
Cost of planting the grass = ₹ 2.50 × 240000 = ₹ 6,00,000
Hence, the required cost = ₹ 6,00,000.

Question 6.
The perimeter of a circle is 176 cm, find its radius.
Solution:
The perimeter of the circle = 176 cm

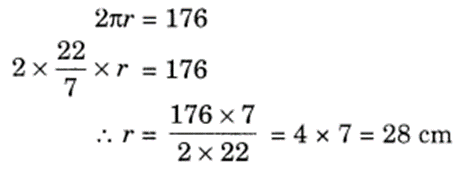
Question 7.
The radius of a circle is 3.5 cm, find its circumference and area.
Solution:
Radius = 3.5 cm
Circumference = 2πr

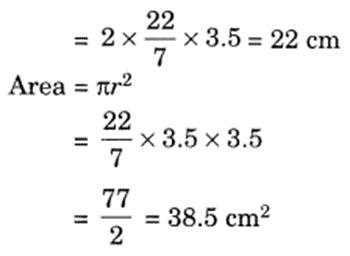
Question 8.
Area of a circle is 154 cm², find its circumference.
Solution:
Area of the circle = 154 cm²

Question 10.
The length of the diagonal of a square is 50 cm, find the perimeter of the square.

Short Answer Type

Question 11.
A wire of length 176 cm is first bent into a square and then into a circle. Which one will have more area?
Solution:
Length of the wire = 176 cm
Side of the square = 176 ÷ 4 cm = 44 cm
Area of the square = (Side)² = (44)² cm² = 1936 cm²
Circumference of the circle = 176 cm

Since 2464 cm² > 1936 cm²
Hence, the circle will have more area.

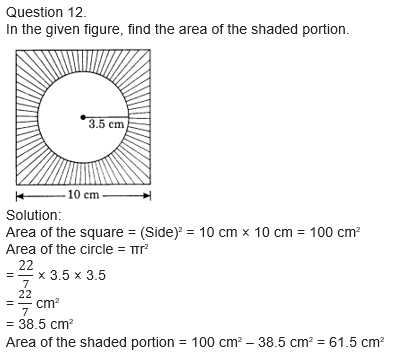
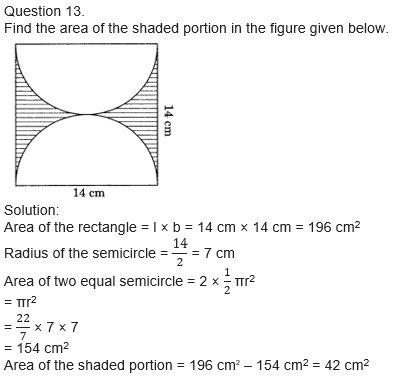
Question 14.
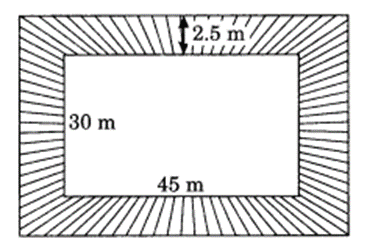
A rectangle park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.

Solution:
Length of the rectangular park = 45 m
Breadth of the park = 30 m
Area of the park = l × 6 = 45m × 30m = 1350 m²
Length of the park including the path = 45 m + 2 × 2.5 m = 50 m
Breadth of the park including the path = 30 m + 2 × 2.5 m = 30m + 5m = 35m
Area of the park including the path = 50 m × 35 m = 1750 m²
Area of the path = 1750 m² – 1350 m² = 400 m²
Hence, the required area = 400 m².

Long Answer Type

Question 17.
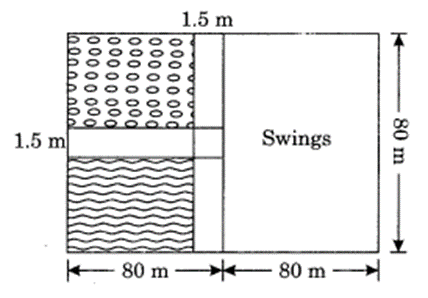
A nursery school playground is 160 m long and 80 m wide. In it 80 m × 80 m is kept for swings and in the remaining portion, there are 1.5 m wide path parallel to its width and parallel to its remaining length as shown in Figure. The remaining area is covered by grass. Find the area covered by grass. (NCERT Exemplar)

Solution:
Area of the playground = l × b = 160 m × 80 m = 12800 m²
Area left for swings = l × b = 80m × 80m = 6400 m²
Area of the remaining portion = 12800 m² – 6400 m² = 6400 m²
Area of the vertical road = 80 m × 1.5 m = 120 m²
Area of the horizontal road = 80 m × 1.5 m = 120 m²
Area of the common portion = 1.5 × 1.5 = 2.25 m²
Area of the two roads = 120 m² + 120 m² – 2.25 m² = (240 – 2.25) m² = 237.75 m²
Area of the portion to be planted by grass = 6400 m² – 237.75 m² = 6162.25 m²
Hence, the required area = 6162.25 m².

Question 18.
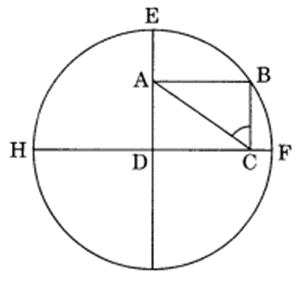
Rectangle ABCD is formed in a circle as shown in Figure. If AE = 8 cm and AD = 5 cm, find the perimeter of the rectangle. (NCERT Exemplar)

Solution:
DE (Radius) = AE + AD = 8 cm + 5 cm = 13 cm
DB = AC = 13 cm (Diagonal of a rectangle are equal)
In right ∆ADC,
AD² + DC² = AC² (By Pythagoras Theorem)
⇒ (5)² + DC² = (13)²
⇒ 25 + DC² = 169
⇒ DC² = 169 – 25 = 144
⇒ DC = √144 = 12 cm
Perimeter of rectangle ABCD = 2(AD + DC)
= 2(5 cm + 12 cm)
= 2 × 17 cm
= 34 cm

Question 19.
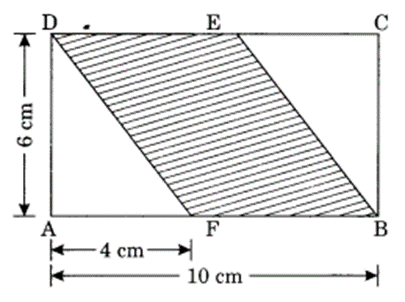
Find the area of a parallelogram-shaped shaded region. Also, find the area of each triangle. What is the ratio of the area of shaded portion to the remaining area of the rectangle?

Question 20.
A rectangular piece of dimension 3 cm × 2 cm was cut from a rectangular sheet of paper of dimensions 6 cm × 5 cm. Find the ratio of the areas of the two rectangles. (NCER T Exemplar)

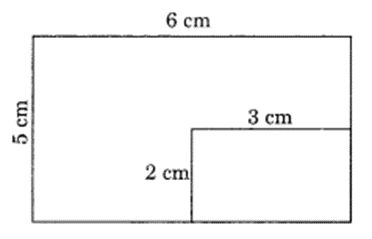
Solution:
Length of the rectangular piece = 6 cm
Breadth = 5 cm
Area of the sheet = l × b = 6 cm × 5 cm = 30 cm²
Area of the smaller rectangular piece = 3 cm × 2 cm = 6 cm²
Ratio of areas of two rectangles = 30 cm² : 6 cm² = 5 : 1

Higher Order Thinking Skills (HOTS) Type

Question 22.
Find the area of the following polygon if AB = 12 cm, AC = 2.4 cm, CE = 6 cm, AD = 4.8 cm, CF = GE = 3.6 cm, DH = 2.4 cm.

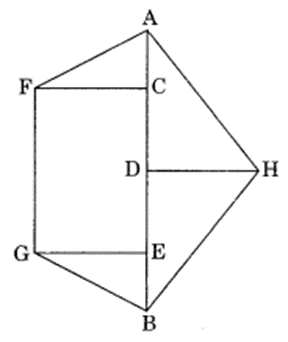
Solution:
BE = AB – AE
= 12 cm – (AC + CE)
= 12 cm – (2.4 cm + 6 cm)
= 12 cm – 8.4 cm
= 3.6 cm


Area of the polygon AFGBH = Area of ∆ACF + Area of rectangle FCEG + Area of ∆GEB + Area of ∆ABH
= 3.6 cm² + 4.32 cm² + 21.6 cm² + 6.48 cm² + 14.4 cm²
= 50.40 cm²
Hence, the required area = 50.40 cm².