Chapter 12 Constructions Ex 12.1 eng

Chapter 12 Constructions Ex 12.1

Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction

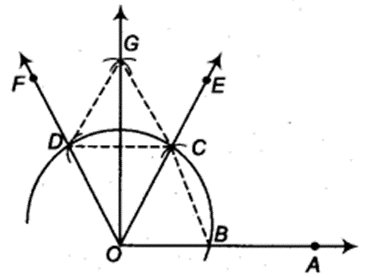
Justification
(i) Join BC.
Then, OC=OB = BC (By construction)
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°

(ii) Join CD.
Then, OD=OC=CD (By construction)
∴ ∆DOC is an equilateral triangle.
∴ ∠DOC = 60°
∴ ∠FOE = 60°

Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction

1. Taking O as centre and some radius, draw an arc of a circle which intersects OA, say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
   

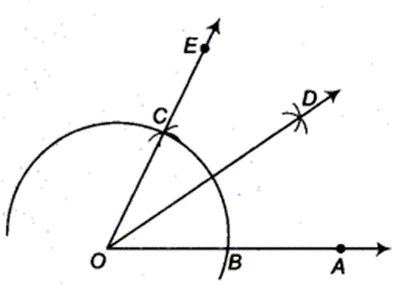
Justification
(i) Join BC. (By construction)
Then, OC = OB = BC
∴ ∆COB is an equilateral triangle.
∴ ∠COB = 60°
∴ ∠EOA = 60°

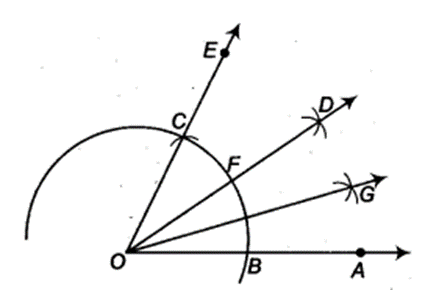
Question 3.

Solution:
(i) Steps of construction

(ii) Steps of construction

(iii) Steps of construction

1. Taking O as centre and some radius, draw an arc of a circle which intersects OA say at a point B.
2. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C..
3. Draw the ray OE passing through C. Then, ∠EOA = 60°.
   

Question 4.
Construct the following angles and verify by measuring them by a protractor
(i) 75°
(ii) 105°
(iii) 135°
Solution:
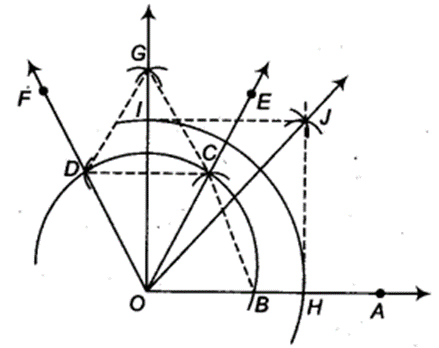
(i) Steps of construction

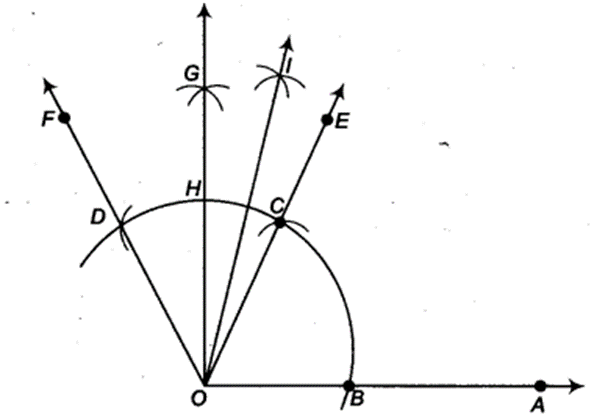
1. On measuring the ∠IOA by protractor, we find that ∠IOA = 15°
   Thus, the construction is verified.

(ii) Steps of construction

1. 
   

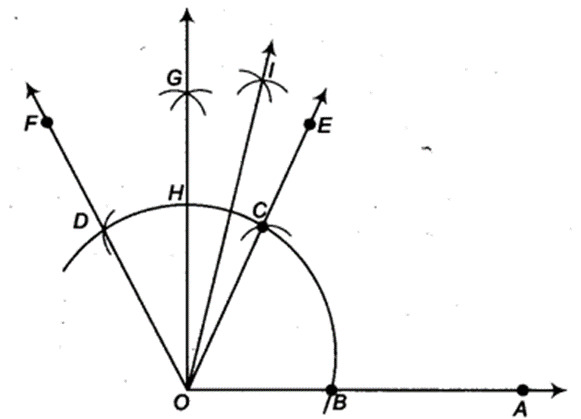
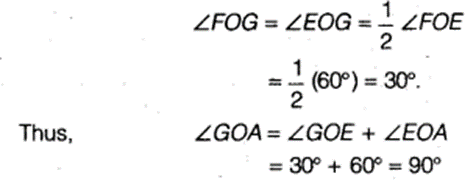
2. Next, taking H and D as centres and with the radius more than 12 HD, draw arcs to intersect each other, say at l.
3. Draw the ray Ol. This ray Ol is the bisector of the ∠FOG, i.e.,
   

1. 
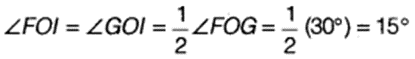
   Thus, ∠lOA = ∠IOG + ∠GOA = 15° + 90° = 105°. On measuring the ∠lOA by protractor, we find that ∠FOA = 105°.
   Thus, the construction is verified.
   

(iii) Steps of construction

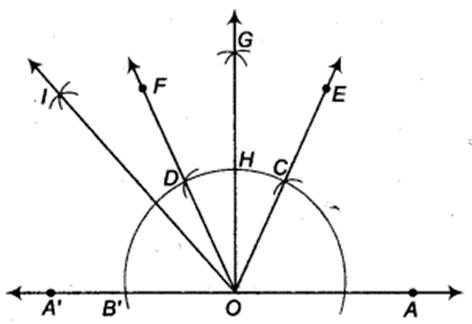
1. Produce AO to A’ to form ray OA’.
2. Taking O as centre and some radius, draw an arc of a circle which intersects OA at a point B and OA’ at a point B’.
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
4. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
5. Draw the ray OE passing through C, then ∠EOA = 60°.
6. Draw the ray OF passing through D, then ∠FOE = 60°.
7. Next, taking C and D as centres and with the radius more than 12 CD, draw arcs to intersect each other, say at G.
8. Draw the ray OGintersecting the arc drawn in step 1 at H. This ray OG is the bisector of the ∠FOE i,e.,
   

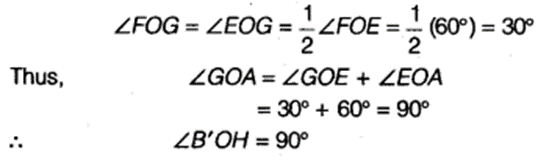
2. Next, taking B’ and H as centres and with the radius more than 12 B’H, drawn arcs to intersect each other, say at l.
3. Draw the ray Ol. This ray Ol is the bisector of the ∠B’OG i.e.,
   

1. 
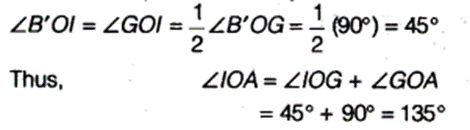
   On measuring the ∠IOA by protractor, we find that ∠lOA = 135°.
   Thus, the construction is verified.

Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
Steps of construction

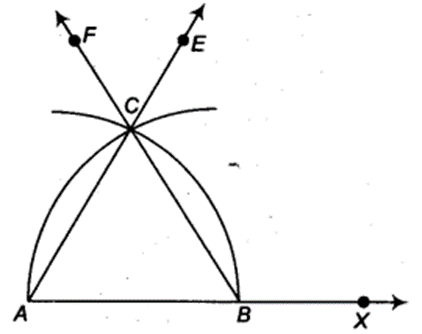
1. Take a ray AX with initial point A From AX, cut off AB = 4 cm.
2. Taking A as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point B.
3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
4. Draw the ray AE passing through C.
5. Next, taking B as centre and radius (= 4 cm), draw an arc of a circle, which intersects AX, say at a point A
6. Taking A as centre and with the same radius as in step 5, draw an arc intersecting the previously drawn arc, say at a point C.
   Draw the ray BF passing through C.
   Then, ∆ ABC is the required triangle with gives side 4 cm.

Justification
AB = BC (By construction)
AB = AC (By construction)
∴ AB = BC = CA
∴ ∆ ABC is an equilateral triangle.
∴ The construction is justified.