Chapter 14 गुणनखंडन Ex 14.2
प्रश्न 1.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –
- a2 + 8a + 16
- p2 – 10p + 25
- 25m2 + 30m + 9
- 49y2 + 84yz + 36z2
- 4x2 – 8x + 4
- 121b2 – 88bc + 16c2
- (l + m)2 – 4lm
- a4 + 2a2b2 + b4
हल:
1. a2 + 8a + 16 = (a)2 + 2 x a x 4 + (4)2
[∴ a2 + 2ab + b2 = (a + b)2]
= (a + 4)2
2. p2 – 10p + 25 = (p)2 – 2 x p x 5 + (5)2
[∴ a2 – 2ab + b2 = (a – b)]
= (p – 5)2
3. 25m2 + 30m + 9 = (5m)2 + 2 x 5m x 3 + (3)2
= (5m + 3)2
4. 49y2 + 84yz + 36z2
= (7y)2 + 2 x 7y x 6z + (6z)2
= (7y + 6z)2
5. 4x2 – 8x + 4 = (2x)2 – 2 x 4x × 2 + (2)2
= (2x – 2)2
6. 121b2 – 88bc + 16c2
= (11b)2 – 2 x 11b x 4c + (4c)2
= (11b – 4c)
7. (l + m)2 – 4lm = l2 + 2lm + m2 – 4lm
= l2 – 2lm + m2
= (l)2 – 2 x 1 x m + (m)2 = (1 – m)
8. a4 + 2a2b2 + b4 = (a2)2 + 2 x a2 x b2 + (a)2
= (a + b)2
प्रश्न 2.
गुणनखण्ड कीजिए –
- 4p2 – 9q2
- 63a2 – 112b2
- 49x2 – 36
- 16x5 – 144x3
- (l + m)2 – (l – m)
- 9x2y2 – 16
- (x2 – 2xy +y2) – z2
- 25a2 – 4b2 + 28bc – 49c2
हल:
1. 4p2 – 9q2
a2 – b2 = (a – b) (a + b)
4p2 – 9q2 = (2p)2 – (3q)2
= (2p – 3q) (2p + 3q)
2. 63a2 – 112b2 = 7 (9a2 – 16b2)
= 7 {(3a)2 – (4b)2}
= 7 (3a – 4b) (3a + 4b)
3. 49x2 – 36 = (7x)2 – (6)2
= (7x – 6) (7x + 6)
4. 16x5 – 144x3 = 16x3 (x2 – 9)
= 16x3 (x2 – 32)
= 16x3 (x – 3) (x + 3)
5. (l + m)2 – (l – m) = [(l + m) – (l – m)][(l + m) – (l – m)]
= (l + m – 1 + m) (l + m + l – m)
= 2m x 2l = 4lm
6. 9x2y2 – 16 = (3xy)2 – (4)2
= (3xy – 4) (3xy + 4)
7. x2 – 2xy + y2 – z2 = (x – y)2 – z2
= [(x – y) – z] [(x – y) + z]
= (x – y – z) (x – y + z)
8. 25a2 – 4b2 + 28bc – 49c2
= 25a2 – (4b2 – 28bc + 49c2)
= 25a2 – [(2b)2 – 2 x 26 x 7c + (7c)2]
= (5a)2 – (2b – 7c)2
= [5a – (2b – 7c)] [5a + (2b – 7c)]
= (5a – 25 + 7c) (5a + 2b – 7c)
प्रश्न 3.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –
- ax2 + bx
- 7p2 + 21q2
- 2x2 + 2xy2 + 2xz2
- am2 + bm2 + bn2 + an2
- (lm + 1) + m + 1
- y (y + z) + 9 (y + z)
- 5y2 – 20y – 8z + 2yz
- 10ab + 4a + 5b + 2
- 6xy – 4y + 6 – 9x.
हल:
1. ax2 + bx = x (ax + b)
2. 7p2 + 21q2 = 7 (p2 + 3q2)
3. 2x2 + 2xy2 + 2xz2 = 2x (x2 + y2 + z2)
4. amv + bm2 + bn2 + an2
= (am2 + bm2) + (bn2 + an2)
= m2 (a + b) + n2 (b+ a)
= (a + b) (m2 + n2)
5. (lm + 1) + m + 1 = 1(m + 1) + 1 (m + 1)
= (m + 1) (1 + 1)
6. y (y + z) + 9 (y + z) = (y + z) (y + 9)
7. 5y2 – 20y – 8z + 2yz
= (5y2 – 20y) + (2yz – 8z)
= 5y (y – 4) + 2z (y – 4).
= (y – 4) (5y + 2z)
8. 10ab + 4a + 56+2
= (10ab + 5b) + (4a + 2)
= 5b (2a + 1) + 2 (2a + 1)
= (2a + 1) (5b + 2)
9. 6xy – 4y + 6 – 9x
= (6xy – 4y) – (9x – 6)
= 2y (3x – 2) – 3 (3x – 2)
= (3x – 2) (2y – 3)
प्रश्न 4.
गुणनखण्ड कीजिए –
- a4 – b4
- p4 – 81
- x4 (y + z)4
- x4 – (x – z)4
- a2 – 2a2b2 + b4
हल:
1. a4 – b4 = (a2)2 – (b2)2
= (a2 + b2) (a2 – b2)
= (a2 + b2) (a + b) (a – b)
2. p4 – 81 = (p2)2 – (9)2
= (p2 + 9) (p2 – 9)
= (p2 + 9) (p + 3) (p – 3)
3. x4 – (y + z)4 = (x2)2 – [(y + 2)2]2
= [x2 – (y + z)2] [x2 + (y + z)2]
= [x – (y + z)] [x + (y + z)] [x2 + (y + z)2]
= (x – y – z) (x + y + z) [x2 + (y + z)2]
4. x4 – (x – z)4 = (x2)2 – [(x – z)2]2
= [x2 – (x – z)2] [x2 + (x – z)]
= [x – (x – z)] [x + (x – z)] [x2 + (x2 – 2x2 + z2)] = (x – x + z) (x + x – z)(2x2 – 2xz + z2)
= z(2x – z) (2x2 – 2xz + z2)
5. a4 – 2a2b2 + b2 = (a2)2 – 2 x a2 x b2 + (b2)2
= [a2 – b2]2
= [(a – b) (a + b)]2
= (a – b)2 (a + b)2
प्रश्न 5.
निम्नलिखित व्यंजकों के गुणनखण्ड कीजिए –
- p2 + 6p + 8
- q2 – 10q + 21
- p2 + 6p – 16
हल:
1. P2 + 6p + 8 = p2 + (4 + 2) p + 8
(∴8 = 4 x 2)
= p2 + 4p + 2p +8
= p (p + 4) + 2 (p + 4)
= (p + 4) (p + 2)
2. q2 – 10q + 21 = q2 – (7 + 3) q + 21
(∴ 21 = 3 x 7)
=q2 – 7q – 3q + 21
= q(q – 7) – 3 (q – 7)
= q (q – 7) (q – 3)
= (q – 3) (q – 7)
3. p2 + 6p – 16 = p2 + (8 – 2)p – 16
(∴ 16 = 8 x 2)
= p2 + 8p – 2p – 16
= p (p + 8) – 2 (p + 8)
= (p + 8) (p – 2)
पाठ्य-पुस्तक पृष्ठ संख्या # 234
प्रयास कीजिए (क्रमांक 14.2)
प्रश्न 1.
भाग दीजिए –
- 24xy23z3 को 6yz2 से
- 63a2b4c6 को 7a2b2c3 से।
हल:
1. 24xy2z3 + 6yz2
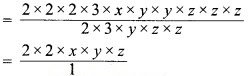
= 4xyz
2. 63a2b4c6 ÷ 7a2b2c3
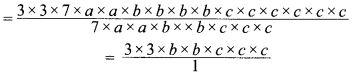
= 9b2c3