Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.1

Chapter 9 बीजीय व्यंजक एवं सर्वसमिकाएँ Ex 9.1

प्रश्न 1.
निम्नलिखित व्यंजकों में से प्रत्येक के पदों एवं गुणांकों को पहचानिए –

(i) 5xyz² – 3ry
(ii) 1 + x + 2
(iii) 4xy² – 4x²y²z² + z²
(iv) 3 – pq + qr – rp
(v) + – xy
(vi) 0.39 – 0.6ab + 0.5b.

उत्तर:

प्रश्न 2.
निम्नलिखित बहुपदों को एकपदी, द्विपद एवं त्रिपद के रूप में वर्गीकृत कीजिए। कौन-सा बहुपद इन श्रेणियों में से किसी में भी नहीं है?
x + y, 1000, x + x² + x³ + 14, 7 + y + 5x, 2y – 3y², 2y – 3y² + 4y², 5x – 4y + 3xy, 4z – 15z²,
ab + be + cd + da, pqr, p²q + pq², 2p + 2q.
हल:

• एकपदी: 1000, Pqr
• द्विपदी: x + y, 2y – 3y², 4 – 15z², P²q – pq², 2p + 24
• त्रिपदी: 7 + y + 5x, 2y – 3y² + 4y³, 5x – 4y + 3xy

वे बहुपद जो उपर्युक्त श्रेणियों में नहीं आते हैं:
x + x² + x³ + x⁴, ab + bc + cd + da

प्रश्न 3.
निम्नलिखित का योग ज्ञात कीजिए –

1. ab – bc, bc – ca, ca – ab
2. a – b + ab, b – c + bc, c – a + ac
3. 2p² – q² – 3pq + 4, 5 + 7pq – 3pq²
4. l² + m², m² + n², n² + l², 2lm + 2mn + 2nl

हल:

1.

2.

3.

4.

अथवा = 2(l² + m² + n² + lm + mn + nl)

प्रश्न 4.

1. 2a – 9ab + 5b – 3 में से 4a – 7ab + 3b + 12 को घटाइए।
2. 5xy – 2yz – 2x + 10xyz में से 3xy + 5ye – 7zx को घटाइए।
3. 18 – 3p – 11q + 5pq – 2pq² + 5p²q में से 4p²q – 3pq + 5pq² – 8p + 7q – 10 को घटाइए।

हल:
1.

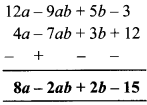
2.

3.

पाठ्य-पुस्तक पृष्ठ संख्या # 150

प्रयास कीजिए (क्रमांक 9.5)

प्रश्न 1.
क्या आप ऐसी और दो परिस्थितियों के बारे में सोच सकते हैं जहाँ हमें बीजीय व्यंजकों को गुणा करना पड़ सकता है?
उत्तर:
हाँ, सोच सकते हैं, जहाँ हमें बीजीय व्यंजकों का गुणा करना पड़ सकता है।

1. चाल और समय (∴ x समय या d = s x t)
2. साधारण ब्याज (∴ S.I. = )

पाठ्य-पुस्तक पृष्ठ संख्या # 151

प्रयास कीजिए (क्रमांक 9.6)

प्रश्न 1.
4x × 5y × 7. ज्ञात कीजिए:
सर्वप्रथम 4x × 5y ज्ञात कीजिए और फिर उसे 7z से गुणा कीजिए, अथवा सर्वप्रथम 5y × 7. ज्ञात कीजिए और इसे 4x से गुणा कीजिए। क्या परिणाम एक जैसा है? आप क्या विचार करते हैं? क्या गुणा करते समय क्रम का महत्व है?
हल:
4x × 5y × 7z = (4x × 5y) × 7z
= 20xy × 7z = 140xy
और 4x × 5y × 7z = 4x × (5y × 7z)
= 4x × 35yz = 140xyz
(4x × 5y) × 7z = 4x × (5y × 7z) = 140xyz
हाँ, परिणाम एक जैसा है।
यहाँ, स्पष्ट है कि बहुपदों का गुणनफल साहचर्य है।
गुणा करते समय क्रम का कोई महत्व नहीं है।

प्रश्न 2.
एक आयत के, जिसकी लम्बाई और चौड़ाई दी हुई है, क्षेत्रफल की सारणी को पूरा कीजिए।
हल: