Chapter 9 Quadrilaterals Ex 9.2
Question 1.
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see figure). AC is a diagonal. Show that

(ii) PQ = SR
(iii) PQRS is a parallelogram.
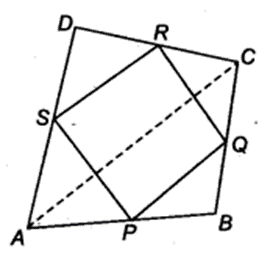
Solution:

(iii) Now, from Eqs. (i) and (iii), we get
PQ || SR
and from Eq. (v), PQ = SR
Since, a pair of opposite sides of a quadrilateral PQRS is equal and parallel.
So, PQRS is a parallelogram.
Hence proved.
Question 2.
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rectangle.
Solution:
Given: ABCD is a rhombus and P, Q, R and S are mid-points of AB, BC, CD and DA
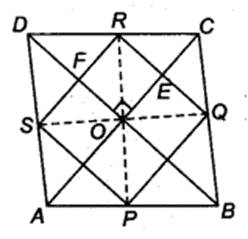
By mid-point theorem,

∴ PQRS is a parallelogram.
Now, we know that diagonals of a rhombus bisect each other at right angles.
∴ ∠EOF = 90°
Now, RQ || BD (By mid-point theorem)
⇒ RE || OF
Also, SP|| AC [From Eq. (i)]
⇒ FR || OE
∴ OERF is a parallelogram.
So, ∠ ERF = ∠EOF = 90°
(Opposite angle of a quadrilateral is equal)
Thus, PQRS is a parallelogram with ∠R = 90°
Hence, PQRS is a rectangle.
Question 3.
ABCD is a rectangle and P, Q, R ans S are mid-points of the sides AB, BC, CD and DA, respectively. Show that the quadrilateral PQRS is a rhombus.
Solution:
Given: ABCD is a rectangle.
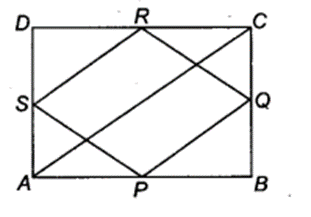
∴ ∠A = ∠B = ∠C= ∠D = 90°
and AD = BC, AB = CD
Also, given P, Q, R and S are mid-points of AB, BC, CD and DA .respectively.

In rectangle ABCD,
AC = BD
∴ PQ = SR …(ii)
Now, in ∆ASP and ∆BQP
AP = BP (Given)
AS = BQ (Given)
∠A = ∠B (Given)
∴ ∆ASP ≅ ∆BQP (By SAS)
∴ SP = PQ (By CPCT)…(ii)
Similarly, in ∆RDS and ∆RCQ,
SD = CQ (Given)
DR = RC (Given)
∠C=∠D (Given)
∴ ∆RDS ≅ ∆RCQ (By SAS)
∴ SR = RQ (By CPCT)…(iii)
From Eqs. (i), (ii) and (iii), it is clear that quadrilateral PQRS is a rhombus.
Question 4.
ABCD is a trapezium in which AB | | DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see figure). Show that F is the mid-point of BC.
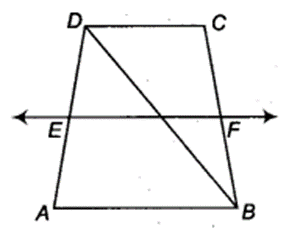
Solution:
Given: ABCD is a trapezium in which AB || CD and E is mid-point of AD and EF || AB.
In ∆ABD, we have
EP\\AB
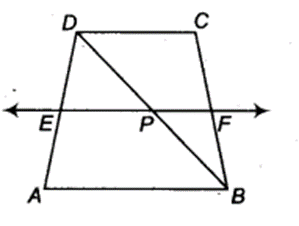
and E is mid-point of AD.
So, by theorem, if a line drawn through the mid-point of one side of a triangle parallel to another side bisect the third side.
∴ P is mid-point of BD.
Similarly, in ∆ BCD, we have,
PF || CD (Given)
and P is mid-point of BD.
So, by converse of mid-point theorem, F is mid-point of CB.
Question 5.
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see figure). Show that the line segments AF and EC trisect the diagonal BD.
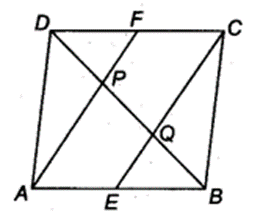
Solution:
Given: ABCD is a parallelogram and E, F are the mid-points of sides AB and CD respectively.
To prove: Line segments AF and EC trisect the diagonal BD.
Proof: Since, ABCD is a parallelogram.

Question 6.
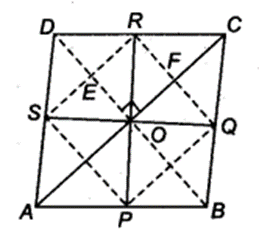
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Solution:
Let ABCD is a quadrilateral and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively, i.e., AS = SD, AP = BP, BQ = CQ and CR = DR. We have to show that PR and SQ bisect each other i.e., SO = OQ and PO = OR.

Question 7.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD ⊥ AC
(iii) CM = MA = 12 AB
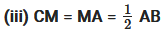
Solution:
Given: ABC is a right angled triangle.
∠C = 90°
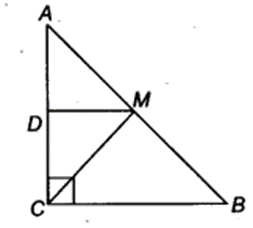
and M is the mid-point of AB.
Also, DM || BC
