Chapter 1 संख्या पद्धति Ex 1.2

Chapter 1 संख्या पद्धति Ex 1.2

प्रश्न 1.
नीचे दिए गए कथन सत्य हैं या असत्य हैं। कारण के साथ अपने उत्तर दीजिए
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
उत्तर:
दिया गया कथन सत्य है क्योंकि प्रत्येक वास्तविक संख्याओं का संग्रह परिमेय और अपरिमेय संख्याओं के संग्रह से मिलकर ही बनता है। अर्थात् अन्य शब्दों में कहा जाए तो परिमेय संख्या एवं अपरिमेय संख्या दोनों ही वास्तविक संख्याओं का भाग होती हैं।

(ii) संख्या रेखा का प्रत्येक बिन्दु √m के रूप का होता है, जहाँ m एक प्राकृत संख्या है।
उत्तर:
दिया गया कथन असत्य है क्योंकि वास्तविक संख्याएँ ….. – 4, – 3, – 2, – 1 संख्या रेखा पर हैं लेकिन ये किसी भी प्राकृत संख्या के वर्गमूल के रूप का नहीं हैं।

(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय संख्या होती है।
उत्तर:
दिया गया कथन असत्य है क्योंकि वास्तविक रेखाओं के संग्रह में परिमेय संख्याओं एवं अपरिमेय संख्याओं का संग्रह होता है। अतः परिमेय संख्याएँ वास्तविक संख्याएँ होते हुए भी अपरिमेय संख्याएँ नहीं हो सकती।

प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
हल:
नहीं। सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं। जैसे -4, 9, 16, 25, 36, …. आदि धनात्मक पूर्णांक हैं लेकिन इनके वर्गमूल एक अपरिमेय संख्या न होकर परिमेय संख्या है, जैसे
√4 = 2 = एक परिमेय संख्या
√9 = 3 = एक परिमेय संख्या
√16 = 4 = एक परिमेय संख्या
√25 = 5 = एक परिमेय संख्या
√36 = 6 = एक परिमेय संख्या आदि।

प्रश्न 3.
दिखाइए कि संख्या रेखा पर 15 को किस प्रकार निरूपित किया जा सकता है?
हल:
∵ 5 = (2)² + (1)²

यहाँ हम √5 की रचना एक समकोण त्रिभुज के कर्ण की लम्बाई के रूप में तथा आधार व लम्ब की लम्बाई के रूप में 2 व 1 एकक (इकाई) के रूप में करेंगे।
माना कि Ox एक संख्या रेखा है जिस पर 0 शून्य (0) को और A, 2 एकक लम्बाई को निरूपित करता है। अब एक रेखा AB, OA पर खींची जो A बिन्दु पर लम्ब है अर्थात् AB ⊥ OA. अब AB = 1 एकक लम्बाई पर B बिन्दु लिखेंगे।

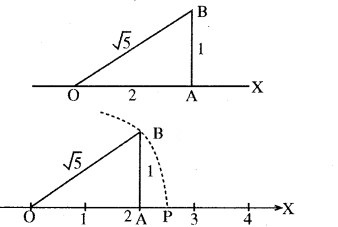
अब OB² = OA² + AB²
= (2)² + (1)²
= 4 + 1 = 5
∴ OB = 15
संख्या रेखा पर निरूपण करने के लिए एक परकार की सहायता से 0 को केन्द्र और OB को त्रिज्या मानकर हम संख्या रेखा पर एक बिन्दु P अंकित करेंगे जो कि संख्या रेखा पर √5 के संगत है। अत: P वह बिन्दु होगा जो अपरिमेय संख्या √5 का निर्धारण करेगा।

प्रश्न 4.
कक्षा के लिए क्रियाकलाप (वर्गमूल सर्पिल की रचना)
हल:

कागज की एक बड़ी शीट लीजिए और नीचे दी गई विधि से वर्गमूल सर्पिल की रचना कीजिए। अर्थात् सबसे पहले एक O बिन्दु लीजिए और एकक लम्बाई का रेखाखण्ड OP₁ खींचिए। आद एकक लम्बाई वाले OP₁
की रचना पर लम्ब रेखाखण्ड P₁P₂ खींचिए अर्थात् OP₁ ⊥ PP₂.

इसी प्रकार OP₂ पर लम्ब रेखाखण्ड P₂P₃ खींचिए व OP₃ पर लम्ब रेखाखण्ड P₃P₄ खींचिए। इस प्रक्रिया को जारी रखते हुए OP_n-1 पर एकक लम्बाई वाला लम्ब रेखाखण्ड खींचकर आप रेखाखण्ड P_n-1 P_n. प्राप्त कर सकते हो। इस प्रकार आप बिन्दु O, P₁, P₂, P₃, …… P_n…… प्राप्त कर लेंगे और उन्हें मिलाकर √2, √3, √4,….. को प्रदर्शित करने वाला एक सुन्दर सर्पिल प्राप्त कर सकते हो।