Chapter 1 Real Numbers Ex 1.2
Question 1.
Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429.
Solutions:
(i) 140
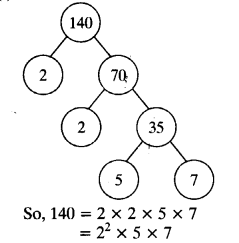
(ii) 156
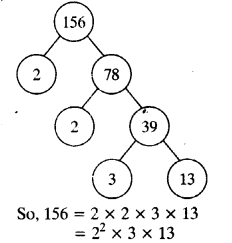
(iii) 3825

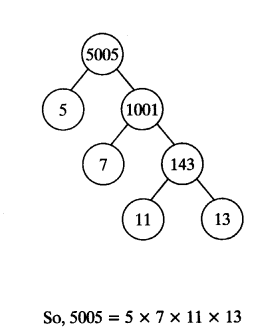
(iv) 5005
![]()
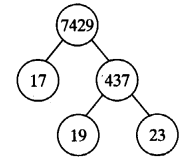
(v) 7429.
So, 7429 = 17 x 19 x 23
Question 2.
Find the LCM and HCF of the following pairs of integers and verify that LCM x HCF = product of two numbers,
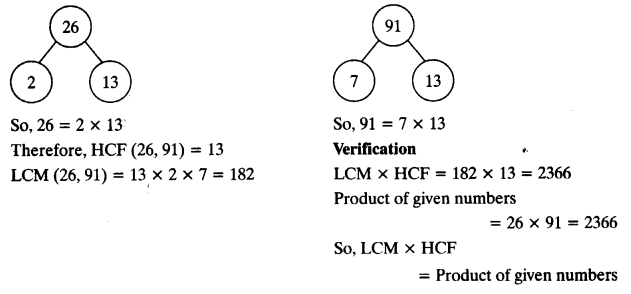
(i) 26 and 91
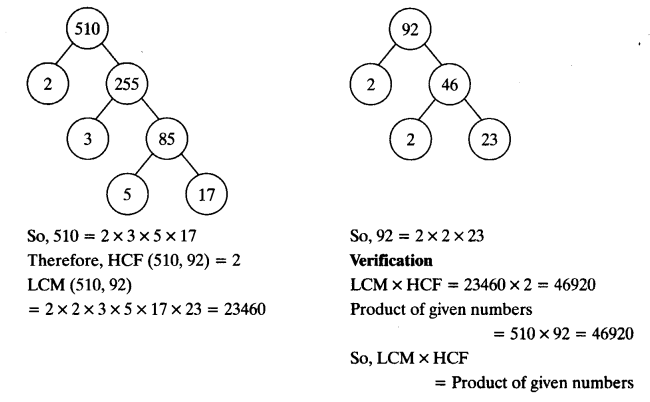
(ii) 510 and 92
(iii) 336 and 54
Solutions:
(i) 26 and 91
(ii) 510 and 92
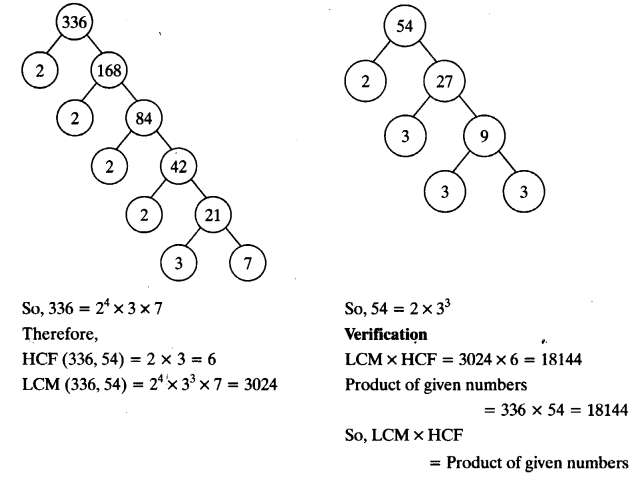
(iii) 336 and 54
Question 3.
Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12,15 and 21
(ii) 17,23 and 29
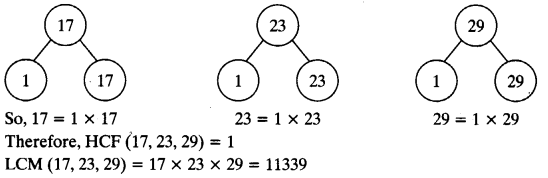
(iii) 8, 9 and 25
Solutions:
(i) 12,15 and 21
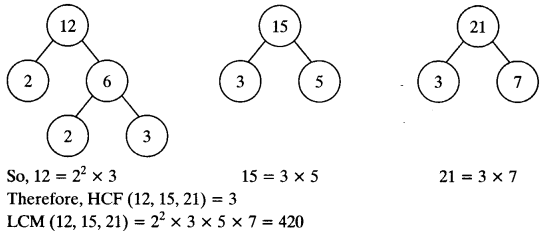
(ii) 17,23 and 29
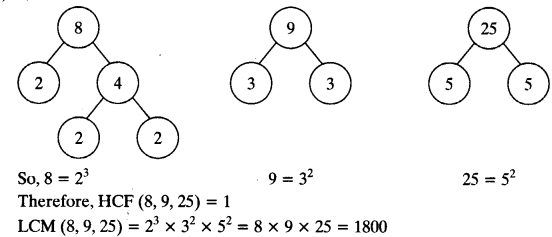
(iii) 8, 9 and 25
Question 4.
Given that HCF (306,657) = 9, find LCM (306, 657).
Solutions:
Given that HCF (306, 657) = 9
We know that LCM x HCF = Product of two numbers
![]()
Question 5.
Check whether 6n can end with the digit 0 for any natural number n.
Solutions:
Since prime factorisation of 6n is given by 6n = (2 x 3)n = 2n x 3n
Prime factorisation of 6n contains only prime numbers 2 and 3.
6n may end with the digit 0 for some ‘n’ if 5 must be in its prime factorisation which is not present.
So, there is no natural number VT for which 6n ends with the digit zero.
Question 6.
Explain why 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are composite numbers.
Solutions:
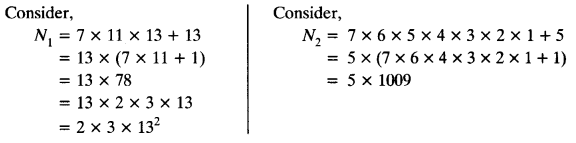
Both N1 and N2 are expressed as a product of primes. Therefore, both are composite numbers.
Question 7.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solutions:
By taking LCM of time taken (in minutes) by Sonia and Ravi, we can get the actual number of minutes after which they meet again at the starting point after both start at same point and of the same time, and go in the same direction.
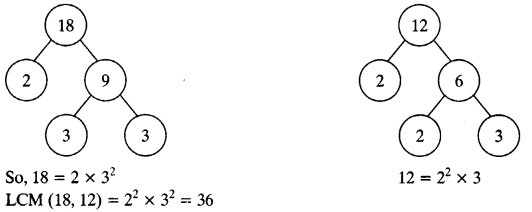
Therefore, both Sonia and Ravi will meet again at the starting point after 36 minutes.