Chapter 10 प्रायोगिक ज्यामिती Ex 10.1

Chapter 10 प्रायोगिक ज्यामिती Ex 10.1

प्रश्न 1.
एक रेखा (मान लीजिए AB) खींचिए और इसके बाहर स्थित कोई बिन्दु C लीजिए। केवल पैमाना (रूलर) और परकार को प्रयोग करते हुए C से होकर AB के समान्तर एक रेखा खींचिए।
हल:
रचना के पद :

1. एक रेखा AB खींची और इसके बाहर एक बिन्दु C लिया।
   
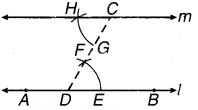
2. रेखा AB पर एक बिन्दुलिया और CD को मिलाया।
3. D को केन्द्र मानकर और उचित त्रिज्या लेकर एक चाप खींचा जो AB को E पर तथा CD को F पर काटता है।
4. C को केन्द्र मानकर और DE के बराबर त्रिज्या लेकर एक चाप खींचा जो CD को G पर काटता है।
5. G को केन्द्र मानकर और EF त्रिज्या लेकर ऊपरी चाप बिन्दु H पर काटा।
6. CH को मिलाते हुए रेखा m खींची। इस प्रकार रेखा m अभीष्ट रेखा है जो m || AB है।

प्रश्न 2.
एक रेखा l खींचिए और l पर स्थित किसी बिन्दु पर l पर लम्ब खींचिए इस लम्ब रेखा पर एक बिन्दु x लीजिए जो l से 4 cm की दूरी पर हो। x से होकर l के समान्तर एक रेखा m खींचिए।
हल:

रचना के पद:

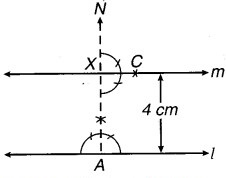
1. एक रेखा l खींची और इस पर एक बिन्दु A लिया।
2. A पर 90° का कोण बनाते हुए l पर लम्बवत् रेखा AN खींची।
3. AN पर कोई बिन्दु x लिया। AX = 4 cm
4. पर 90° का कोण बनाकर AN पर लम्ब खींचा।, m || l अभीष्ट रेखा है, जो x से होकर जाती है।

प्रश्न 3.
मान लीजिए l एक रेखा है और Pएक बिन्दु है: जो l पर स्थित नहीं है। Pसे होकर l के समान्तर एक रेखा m खींचिए। अब P को l के किसी बिन्दुए से जोड़िए। m पर कोई अन्य बिन्दु R चुनिए। R से होकर, PQ के समान्तर एक रेखा खींचिए। मान लीजिए यह रेखा l से बिन्दु पर मिलती है। समान्तर रेखाओं के इन दोनों युग्मों से क्या आकृति बनती
हल:
रचना के पद:

1. एक रेखा l खींची और इसके बाहर कोई बिन्दु P लिया।
2. रेखा l पर कोई बिन्दुए लिया और PQ को मिलाया।
3. P से m || l खींची।
4. रेखा m पर कोई बिन्दु R लिया।
5.  R से RS || PQ इस प्रकार खींची कि यह l पर 5 से मिले।

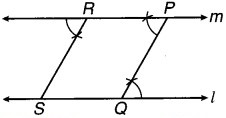
∴ l || m अत: RP || SQ
साथ ही PQ || RS
∴ PQRS एक समान्तर चतुर्भुज है।

पाठ्य-पुस्तक पृष्ठ संख्या # 214

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
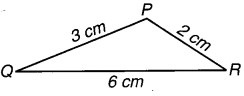
एक विद्यार्थी ने एक ऐसा त्रिभुज खींचने का प्रयत्न किया, जिसकी रफ आकृति यहाँ दी गई है। पहले उसने QR खींचा। फिर उसने 0 को केन्द्र मानकर और 3 cm त्रिज्या लेकर एक चाप खींचा तथा R को केन्द्र मानकर और 2 cm त्रिज्या लेकर एक अन्य चाप खींचा। परन्तु वह नहीं प्राप्त कर सका। इसका क्या कारण है ? इस प्रश्न से सम्बन्धित किसी गुण को आप जानते हैं ? क्या ऐसे त्रिभुज का अस्तित्व है? (त्रिभुज के इस गुण को याद कीजिए : किसी त्रिभुज की दो भुजाओं का योग सदैव तीसरी भुजा से बड़ा होता है।) सोचिए क्या यह सही है ?

हल:
इन मापों से त्रिभुज बनना असम्भव है। क्योंकि त्रिभुज का बनना तभी सम्भव है जबकि त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा हो, परन्तु यहाँ 2 cm + 3 cm = 5cm < 6 cm

अत: ऐसे त्रिभुज का कोई अस्तित्व नहीं है।