Chapter 10 प्रायोगिक ज्यामिती Ex 10.3

Chapter 10 प्रायोगिक ज्यामिती Ex 10.3

प्रश्न 1.
∆ DEF की रचना कीजिए, ताकि DE = 5 cm, DF = 3 cm और m ∠EDF = 90° हो।
हल:
रचना के पद:

1. सर्वप्रथम आधार DE = 5 cm का एक रेखाखण्ड खींचा।
   
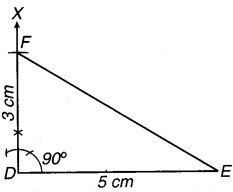
2. DE के बिन्दु D पर 90° का कोण बनाते हुए एक किरण DX खींची तथा जिसमें से DF = 3 cm का रेखाखण्ड काटा।
3. F और E को मिलाया।

अतः प्राप्त ∆ DEF अभीष्ट त्रिभुज है।

प्रश्न 2.
एक समद्विबाहु त्रिभुज की रचना कीजिए, जिसकी प्रत्येक समान भुजा की लम्बाई 6.5 cm हो और उनके बीच का कोण 110° का हो।
हल:
रचना के पद:

1. सर्वप्रथम आधार AB = 6.5 cm का रेखाखण्ड खींचा।
   
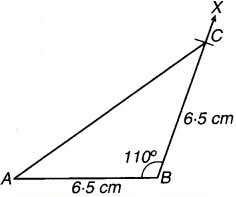
2. AB के बिन्दु B पर ∠ABX = 110° का कोण बनाते हुए एक किरण BX खींची।
3. रेखा BX में से BC = 6.5 cm काटकर रेखाखण्ड BC प्राप्त किया।
4. C और A को मिलाया। अतः प्राप्त ∆ABC अभीष्ट समद्विबाहु त्रिभुज है।

प्रश्न 3.
BC = 7.5 cm,AC = 5 cm और m∠C = 60° वाले ∆ABC की रचना कीजिए।
हल:
रचना के पद :

1. सर्वप्रथम आधार BC = 7.5 cm का एक रेखाखण्ड खींचा।
2. BC के बिन्दु C पर ∠BCX = 60° बनाते हुए एक किरण CX खींची।
3. किरण CX में से AC = 5 cm काटकर रेखाखण्ड AC प्राप्त किया।
4. A व B को मिलाया।

अतः प्राप्त ∆ ABC अभीष्ट त्रिभुज है।

पाठ्य-पुस्तक पृष्ठ संख्या # 218

सोचिए, चर्चा कीजिए एवं लिखिए

प्रश्न 1.
उपर्युक्त उदाहरण में, एक भुजा की लम्बाई और दो कोणों के माप दिए गए थे। अब निम्नलिखित समस्या का अध्ययन कीजिए:
∆ ABC में यदि AC = 7 cm, m∠A = 60° और m∠B = 50° है, तो क्या आप त्रिभुज की रचना कर सकते हैं ? (त्रिभुज का कोण योग गुण आपकी सहायता कर सकता है।)
हल:
यहाँ, हमें AC, ∠A तथा ∠B दिया हुआ है। त्रिभुज के कोण योग गुणं से तीसरा कोण ∠C ज्ञात करेंगे।
∴ m∠A + m∠B + m∠C = 180°
∴ 60° + 50° + m∠C = 180°
या m∠C = 180° – (60° + 50°) = 70°
इन मापों के आधार पर ∆ ABC की रचना की जा सकती है।