Chapter 10 Circles Ex 10.1
Question 1.
How many tangents can a circle have?
Solution:
There can be infinitely many tangents to a circle.
Question 2.
Fill in the blanks:
(i) A tangent to a circle intersects it in ………… point(s).
(ii) A line intersecting a circle in two points is called a ………… .
(iii) A circle can have parallel tangents at the most ………… .
(iv) The common point of a tangent to a circle and the circle is called ……….. .
Solution:
(i) One
(ii) Secant
(iii) Two
(iv) Point of contact.
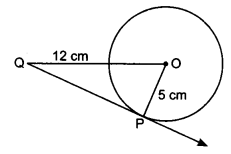
Question 3.

Solution:

Question 4.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
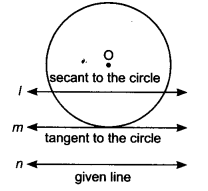
A line m is parallel to the line n and a line l which is secant is parallel to the given line.