Chapter 10 Visualising Solid Shapes Exercise 10.3
Question 1.
Can a polyhedron have for its faces
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution:
(i) No, because polyhedron must have edges meeting at vertices which are points.
(ii) Yes, because all the edges are meeting at the vertices.
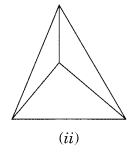
(iii) Yes, because all the eight edges meet at the vertices.
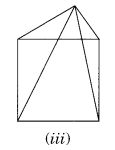
Question 2.
Is it possible to have a polyhedron with any given number of faces?
(Hint: Think of a pyramid)
Solution:
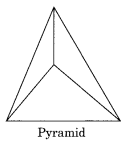
Yes, it is possible if the number of faces is greater than or equal to 4.
Example: Pyramid which has 4 faces.
Question 3.
Which are prisms among the following?
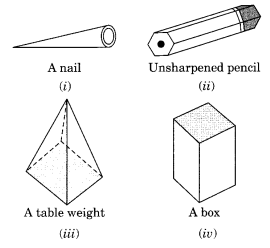
Solution:
Only (ii) unsharpened pencil and (iv) a box are the prism.
Question 4.
(i) How are prisms and cylinders alike?
(ii) How are pyramids and cones alike?
Solution:
(i) If the number of sides in a prism is increased to certain extent, then the prism will take the shape of cylinder.
(ii) If the number of sides of the pyramid is increased to same extent, then the pyramid becomes a cone.
Question 5.
Is a square prism same as a cube? Explain.
Solution:
Every square prism cannot be cube. It may be cuboid also.
Question 6.
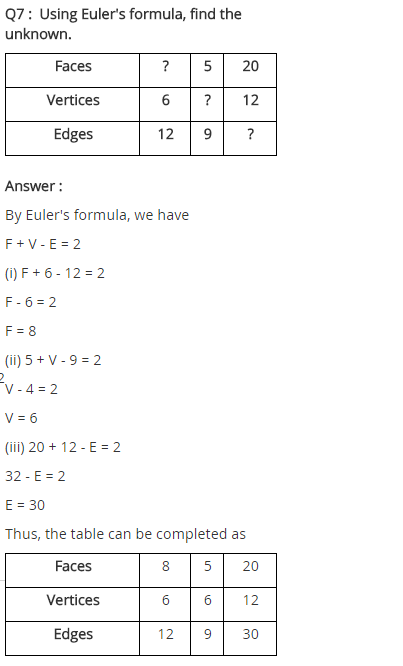
Verify Euler’s formula for these solids.
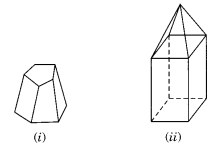
Solution:
(i) Faces = 7
Sides = 15
Vertices = 10
Euler’s formula: F + V – E = 2
⇒ 7 + 10 – 15 = 2
⇒ 2 = 2
Hence, Euler’s formula is verified.
(ii) Faces = 9
Sides = 16
Vertices = 9
Euler’s Formula: F + V – E = 2
⇒ 9 + 9 – 16 = 2
⇒ 2 = 2
Hence, Euler’s formula is verified.
Question 7.
Using Euler’s formula find the unknown.
Faces | ? | 5 | 20 |
Vertices | 6 | ? | 12 |
Edges | 12 | 9 | ? |
Solution:
Faces | 8 | 5 | 20 |
Vertices | 6 | 6 | 12 |
Edges | 12 | 9 | 30 |
Using Eulers Formula: F + V – E = 2
Question 8.
Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution:
Here faces = 10, Edges = 20, Vertices = 15
According to Euler’s Formula:
F + V – E = 2
⇒ 10 + 15 – 20 = 25 – 20
⇒ 5 ≠ 2
A polyhedron do not have 10 Faces, 20 Edges and 15 Vertices.