Chapter 11 परिमाप और क्षेत्रफल Ex 11.3
प्रश्न 1.
निम्न त्रिज्याओं वाले वृत्तों की परिधि ज्ञात कीजिए (π = लीजिए):
(a) 14 cm
(b) 28 cm
(c) 21 cm
हल:

हल:

प्रश्न 3.
यदि एक वृत्ताकार शीट की परिधि 154 मी हो, तो इसकी त्रिज्या ज्ञात कीजिए। शीट का क्षेत्रफल भी ज्ञात कीजिए
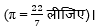
हल:
यहाँ, वृत्त की परिधि = 154 m,
माना कि त्रिज्या = r m
∴ वृत्त की परिधि = 2πr = 154
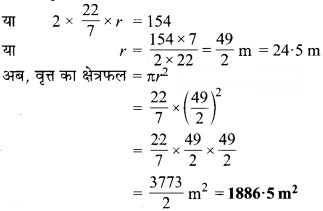
प्रश्न 4.
21 m व्यास वाले एक वृत्ताकार बगीचे के चारों ओर माली बाड़ लगाना चाहता है। खरीदे जाने वाले आवश्यक रस्से की लम्बाई ज्ञात कीजिए, यदि वह 2 पूरे चक्कर की बाड़ बनाना चाहता है। ₹ 4 प्रति मीटर की दर से रस्से पर व्यय ज्ञात कीजिए
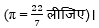
हल:

प्रश्न 5.
4 cm त्रिज्या वाली एक वृत्ताकार शीट में से 3cm त्रिज्या वाले एक वृत्त को निकाल दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए)।
हल:
वृत्ताकार शीट की त्रिज्या R = 4cm (बाहरी त्रिज्या)
शीट में से निकाले गये वृत्त की त्रिज्या r = 3 cm (भीतरी त्रिज्या)
∴ शेष शीट का क्षेत्रफल = बाहरी वृत्त का क्षेत्रफल – भीतरी वृत्त का क्षेत्रफल
= πR2 – πr2
= π (R2 – r2) = π (R + r) (R – r)
= 3.14 × (4 + 3) (4 – 3)
= 3.14 × 7 × 1 = 21.98 cm2
प्रश्न 6.
साइमा 1.5 m व्यास वाले एक वृत्ताकार टेबल कवर के चारों ओर किनारी लगाना चाहती है। आवश्यक किनारी की लम्बाई ज्ञात कीजिए और ₹15 प्रति मीटर की दर से किनारी लगाने का व्यय ज्ञात कीजिए (π = 3.14 लीजिए)।
हल:

प्रश्न 7.
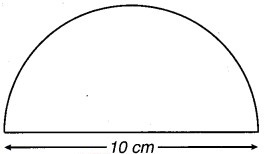
दी गई आकृति व्यास के साथ एक अर्द्धवृत्त है। इसका परिमाप ज्ञात कीजिए।
हल:
अर्द्धवृत्त का व्यास = 10 cm
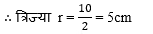

प्रश्न 8.
₹ 15 प्रति वर्ग मीटर की दर से 1.6m व्यास वाले एक वृत्ताकार टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय ज्ञात कीजिए (π = 3.14 लीजिए)।
हल:
टेबल के ऊपरी सतह का व्यास = 1.6m
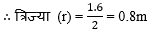
टेबल के ऊपरी सतह का क्षेत्रफल
= πr2 = 3.14 × (0.8)2
= 3.14 × 0.8 × 0.8 m2
∵ पॉलिश की दर = ₹ 15/m2
∴ टेबल के ऊपरी सतह पर पॉलिश कराने का व्यय
= ₹15 × 3.14 × 0.8 × 0.8
= ₹30.144
अत: पॉलिश कराने का अभीष्ट व्यय
= ₹30.14(लगभग)
प्रश्न 9.
शाझली 44 cm लम्बाई वाला एक तार लेती है और उसे एक वृत्त के आकार में मोड़ देती है। उस वृत्त की त्रिज्या ज्ञात कीजिए। इसका क्षेत्रफल भी ज्ञात कीजिए। यदि इस तार को दुबारा एक वर्ग के आकार में मोड़ा जाता है, तो इसकी प्रत्येक भुजा की लम्बाई क्या होगी?
कौन-सी आकृति अधिक क्षेत्रफल घेरती है-वृत्त या वर्ग ?
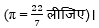
हल:
यहाँ, तार की लम्बाई = 44 cm,
‘माना कि वृत्त की त्रिज्या = r
∵ तार द्वारा बने वृत्त की परिधि = 2πr
∴ 2πr = 44
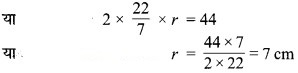

प्रश्न 10.
14 cm त्रिज्या वाली एक वृत्ताकार गत्ते की शीट में से 3.5 cm त्रिज्या वाले दो वृत्तों को और 3 cm लम्बाई तथा 1 cm चौड़ाई वाले एक आयत को निकाल दिया जाता है (जैसा कि संलग्न आकृति में दिखाया गया है)। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए
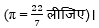

हल:

अत: दो छोटे वृत्तों का क्षेत्रफल
= 2 × 38.5 cm2 = 77 cm2
पुनः छोटे आयत की लम्बाई = 3 cm, चौड़ाई = 1 cm
∴ आयत का क्षेत्रफल = 3 × 1 = 3 cm2
∴ शीट से काटा गया कुल क्षेत्रफल
= 77 cm2 + 3 cm2 = 80 cm2
अतः, शीट के शेष भाग का क्षेत्रफल
= 616 cm2 – 80 cm2
= 536 cm2
प्रश्न 11.
6 cm भुजा वाले एक वर्गाकार ऐल्युमिनियम शीट के टुकड़े में से 2 cm त्रिज्या वाले एक वृत्त को काट दिया जाता है। शीट के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
(π = 3.14 लीजिए)
हल:
वर्ग की भुजा = 6 cm
∴ वर्ग का क्षेत्रफल = a × a = 6 × 6 = 36 cm2
शीट में से काटे गये वृत्त की त्रिज्या = 2 cm
∴ वृत्त का क्षेत्रफल = πr2 = 3.14 × 2 × 2
= 12.56 cm2
शीट के शेष भाग का क्षेत्रफल = 36 cm2 – 12.56 cm2
= 23.44 cm2
प्रश्न 12.
एक वृत्त की परिधि 31.4.cm है। वृत्त की त्रिज्या और क्षेत्रफल ज्ञात कीजिए (π = 3.14 लीजिए)।
हल:
यहाँ, वृत्त की परिधि = 31.4 cm
माना कि वृत्त की त्रिज्या = r
∴ 2πr = 31.4
या 2 × 3.14 × r = 314
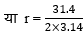
= 5 cm
अतः वृत्त की अभीष्ट त्रिज्या = 5 cm
अब, वृत्त का क्षेत्रफल = πr2
3.14 × 5 × 5
= 78.5 cm2
प्रश्न 13.
एक वृत्ताकार फूलों की क्यारी के चारों ओर 4m चौड़ा पथ है तथा फूलों की क्यारी का व्यास 66 m है। इस पथ का क्षेत्रफल ज्ञात कीजिए (π = 3.14 लीजिए)।
हल:
यहाँ, फूलों की क्यारी का व्यास = 66 m
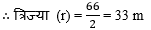
∵ चारों ओर मार्ग की चौड़ाई = 4 m

∴ बाहरी वृत्त की त्रिज्या (R) = 33 m + 4 m
= 37 m
∴ शेष भाग का क्षेत्रफल = πR2 – πr2
= π (R2 – r2)
= 3.14 × (372 – 332)
= 3.14 × (37 + 33) (37 – 33)
= 3.14 × 70 × 4 = 879.2 m2
अतः पथ का अभीष्ट क्षेत्रफल = 879.2 m2
प्रश्न 14.
एक वृत्ताकार फूलों के बगीचे का क्षेत्रफल 314 m2 है। बगीचे के केन्द्र में एक घूमने वाला फव्वारा (Sprinkler) लगाया जाता है जो अपने चारों ओर 12 m त्रिज्या के क्षेत्रफल में पानी का छिड़काव करता है। क्या फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा ? (π = 3.14 लीजिए)
हल:
वृत्ताकार बगीचे का क्षेत्रफल = 314 m2
माना कि बगीचे की त्रिज्या = r m
∴ बगीचे का क्षेत्रफल = πr2 = 314
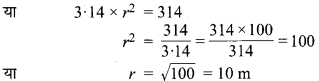
अब फव्वारे द्वारा घिरे क्षेत्र की त्रिज्या = 12 m
∵ 12 m > 10 m
हाँ, फव्वारा पूरे बगीचे में पानी का छिड़काव कर सकेगा।
प्रश्न 15.
आकृति में अन्तः और बाह्य वृत्तों की परिधि ज्ञात कीजिए (π = 3.14 लीजिए)
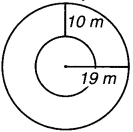
हल:
यहाँ, बाह्य वृत्त की त्रिज्या (R) = 19 m
∴ बाह्य वृत्त की परिधि = 2πR
= 2 × 3.14 × 19 m
= 119.32 m
अन्त: वृत्त की त्रिज्या (r) = 19m – 10 m = 9m
∴ अन्तः वृत्त की परिधि = 2πr
= 2 × 3.14 × 9
= 56.52 m
प्रश्न 16.
28 cm त्रिज्या वाले एक पहिए को 352 m दूरी · तय करने के लिए कितनी बार घुमाना पड़ेगा?
हल:
पहिए की त्रिज्या (r) = 28 cm
∴ पहिए की परिधि = 2πr

∵ पहिए द्वारा 1 चक्कर में तय की गई दूरी = 176 cm
∵ पहिए द्वारा तय कुल दूरी = 352 m = 35,200 cm

अतः पहिया 352 m की दूरी 200 चक्करों में तय करेगा।
प्रश्न 17.
एक वृत्ताकार घड़ी की मिनट की सुई की लम्बाई 15 cm है। मिनट की सुई की नोंक 1 घण्टे में कितनी दूरी तय करेगी। (π = 3.14 लीजिए)
हल:
∵ मिनट की सुई की लम्बाई = 15 cm
∴ मिनट की सुई की नोंक द्वारा बनाए गए वृत्त की त्रिज्या
(r) = 15 cm
इस प्रकार, बने वृत्त की परिधि
= 2πr = 2 × 3.14 × 15 = 94.2 cm
∵ मिनट की सुई 1 घण्टे में 1 चक्कर लगाती है।
अत: मिनट की सुई की नोंक द्वारा 1 घण्टे में चली गई अभीष्ट दूरी = 94.2 cm
पाठ्य-पुस्तक पृष्ठ संख्या # 241
इन्हें कीजिए
प्रश्न 1.
निम्न को बदलिए :
(i) 50 cm2 को mm2 में
(ii) 2 ha को m2 में
(iii) 10 m2 को cm2 में
(iv) 1000 cm2 को mm2 में
हल:
(i) ∵ 1 cm2 = (10 × 10) mm2 = 100 mm2
∴ 50 cm = (50 × 100) mm2
= 5000 mm2
(ii) ∵ 1 हेक्टेअर = (100 × 100) m2 = 10000 m2
∴ 2 हेक्टेअर = 2 × 10000 = 20000 m2
(iii) ∵ 1m2 = (100 × 100) cm2
= 10000 cm2
∴ 10 m2 = 10 × 10000 = 100000 cm2
(iv) ∵ 1 cm2 = (10 × 10) mm2 = 100 mm2
∴ 1000 cm2 = 1000 × 100 = 100000 mm2
पाठ्य-पुस्तक पृष्ठ संख्या # 243-244