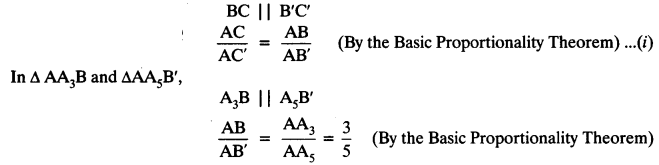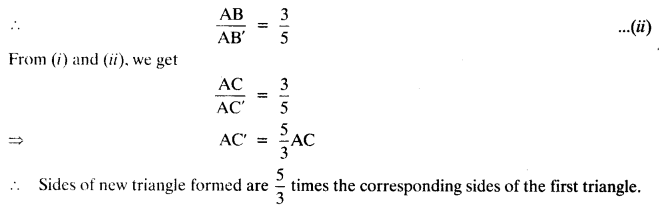Chapter 11 Constructions Ex 11.1

Chapter 11 Constructions Ex 11.1

In each of the following, give the justification of the construction also:

Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
Steps of Construction:
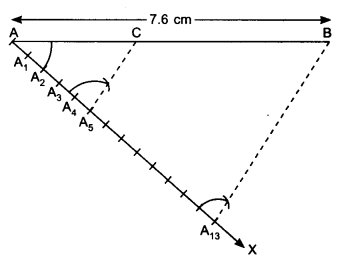
1. Draw a line segment AB = 7.6 cm.
2. Draw an acute angle BAX on base AB. Mark the ray as AX.
3. Locate 13 points A₁, A₂, A₃, …… , A₁₃ on the ray AX so that AA₁ = A₁A₂ = ……… = A₁₂A₁₃
4. Join A₁₃ with B and at A₅ draw a line ∥ to BA₁₃, i.e. A₅C. The line intersects AB at C.
5. On measure AC = 2.9 cm and BC = 4.7 cm.

Justification:
In ∆AA₅C and ∆AA₁₃B,

∴ AC : BC = 5 : 8

Question 2.

Solution:
Steps of Construction:
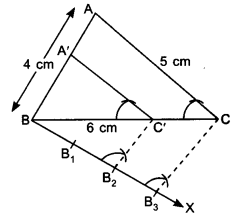
1. Construct a ΔABC with AB = 4 cm, BC = 6 cm and AC = 5 cm.
2. Draw an acute angle CBX on the base BC at point B. Mark the ray as BX.
3. Mark the ray BX with B₁, B₂, B₃ such that
BB₁ = B₁B₂ = B₂B₃
4. Join B₃ to C.
5. Draw B₂C’ ∥ B3C, where C’ is a point on BC.
6. Draw C’A’ ∥ AC, where A’ is a point on BA.
7. ΔA’BC’ is the required triangle.

Justification: In ∆A’BC and ∆ABC,

Question 3.

Solution:
Steps of Construction:
1. Draw a ΔABC with AB = 5 cm, BC = 7 cm and AC = 6 cm.
2. Draw an acute angle CBX below BC at point B.
3. Mark the ray BX as B₁, B₂, B₃, B₄, B₅, B₆ and B₇ such that BB₁= B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
4. Join B₅ to C.
5. Draw B₇C’ parallel to B₅C, where C’ is a point on extended line BC.
6. Draw A’C’ ∥ AC, where A’ is a point on extended line BA.
A’BC’ is the required triangle.

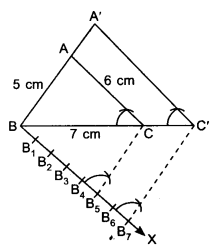
Justification: In ∆ABC and ∆A’BC’,

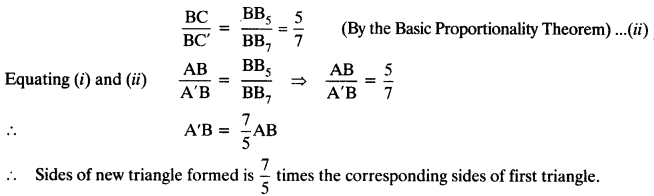
Question 4.

Solution:
Steps of Construction:
1. Draw base AB = 8 cm.
2. Draw perpendicular bisector of AB. Mark CD = 4 cm, on ⊥ bisector where D is mid-point on AB.
3. Draw an acute angle BAX, below AB at point A.
4. Mark the ray AX with A₁, A₂, A₃ such that AA₁ =A₁A₂ = A₂A₃
5. Join A₂ to B. Draw A₃B’ ∥ A₂ B, where B’ is a point on extended line AB.
6. At B’, draw B’C’ 11 BC, where C’ is a point on extended line AC.
7. ∆AB’C’ is the required triangle.

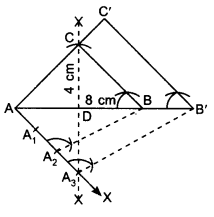
Justification: In ∆ABC and ∆A’BC’,

Question 5.

Solution:
Steps of Construction:
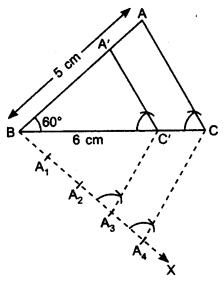
1. Draw a line segment BC = 6 cm and at point B draw an ∠ABC = 60°.
2. Cut AB = 5 cm. Join AC. We obtain a ΔABC.
3. Draw a ray BX making an acute angle with BC on the side opposite to the vertex A.
4. Locate 4 points A₁, A₂, A₃ and A₄ on the ray BX so that BA₁ = A₁A₂ = A₂A₃ = A₃A₄.
5. Join A₄ to C.
6. At A₃, draw A₃C’ ∥ A₄C, where C’ is a point on the line segment BC.
7. At C’, draw C’A’ ∥ CA, where A’ is a point on the line segment BA.
∴ ∆A’BC’ is the required triangle.

Question 6.

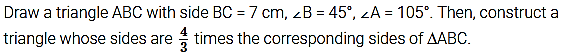
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180°
⇒ 105° + 45° + ∠C = 180°
⇒ 150° + ∠C = 180°
⇒ ∠C = 30°
Steps of Construction:
1. Draw a line segment BC = 7 cm. At point B, draw an ∠B = 45° and at point C, draw an ∠C = 30° and get ΔABC.
2. Draw an acute ∠CBX on the base BC at point B. Mark the ray BX with B₁, B₂, B₃, B₄, such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄
3. Join B₃ to C.
4. Draw B₄C’ ∥ B₃C, where C’ is point on extended line segment BC.
5. At C’, draw C’A’ ∥ AC, where A’ is a point on extended line segment BA.
6. ∆A’BC’ is the required triangle.

Justification: In ∆ABC and ∆A’BC’,

Question 7.

Solution:
Steps of Construction:
1. Draw a right angled ∆ABC with AB = 4 cm, AC = 3 cm and ∠A = 90°.
2. Make an acute angle BAX on the base AB at point A.
3. Mark the ray AX with A₁, A₂, A₃, A₄, A₅ such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
4. Join A₃B. At A₅, draw A₅B’ ∥ A₃B, where B’ is a point on extended line segment AB.
5. At B’, draw B’C’ ∥ BC, where C’ is a point on extended line segment AC.
6. ∆AB’C’ is the required triangle.

Justification:
In ∆ABC and ∆AB’C’,