Chapter 2 बहुपद Ex 2.4
प्रश्न 1.
बताइए कि निम्नलिखित बहुपदों में से किस बहुपद का एक गुणनखण्ड x + 1 है
(i) x3 + x2 + x + 1
हल:
माना कि p (x) = x3 + x2 + x + 1
यहाँ x + 1 का शून्यक – 1 है
तब p (- 1) = (- 1)3 + (- 1)2 + (- 1) + 1
= – 1 + 1 – 1 + 1
= 0
अतः गुणनखण्ड प्रमेय के अनुसार x + 1, बहुपद x3 + x2 + x + 1 का एक गुणनखण्ड है।
(ii) x4 + x3 + x2 + x + 1
हल:
माना कि p (x) = x4 + x3 + x2 + x + 1
यहाँ x + 1 का शून्यक – 1 है
तब p (- 1) = (-1)4 + (- 1)3 + (- 1)2 + (-1) + 1
= 1 – 1 + 1 – 1 + 1
= 1 ≠ 0
अतः गुणनखण्ड प्रमेय के अनुसार x + 1, बहुपद x4 + x3 + x2 + x + 1 का एक गुणनखण्ड नहीं है।
(iii) x4 + 3x3 + 3x2 + x + 1
हल:
माना कि p (x) = x4 + 3x3 + 3x2 + x + 1
यहाँ x + 1 का शून्यक – 1 है
तब p (- 1) = (-1)4 + 3 (- 1)3 + 3 (-1)2 + (-1) + 1
= 1 – 3 + 3 – 1 + 1
= 1 ≠ 0
अतः गुणनखण्ड प्रमेय के अनुसार x + 1, बहुपद x4 + 3x3 + 3x2 + x + 1 का एक गुणनखण्ड नहीं है।
(iv) x3 – (2 + √2)x + √2
हल:
माना कि p (x) = x3 – (2 + √2)x + √2
यहाँ x + 1 का शून्यक – 1 है
तब p (- 1) = (- 1)3 – (- 1) – (2 + √2) (-1) + √2
= – 1 – 1 + 2 + √2 + √2
= 2√2 + 0
अतः गुणनखण्ड प्रमेय के अनुसार x + 1, बहुपद x3 – (2 + √2)x + √2 का एक गुणनखण्ड नहीं है।
प्रश्न 2.
गुणनखण्ड प्रमेय लागू करके बताइए कि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में g (x), p (x) का एक गुणनखण्ड है या नहीं
(i) p (x) = 2x3 + x2 – 2x – 1, g (x) = x + 1
हल:
प्रश्नानुसार
p (x) = 2x3 + x2 – 2x – 1
तथा g (x) = x + 1
अब x + 1 = 0 या x = – 1
x = – 1 का मान p (x) में प्रतिस्थापित करने पर
p (- 1) = 2 (- 1)3 + (- 1)2 – 2 (- 1) – 1
= – 2 + 1 + 2 – 1
= 0
अत: गुणनखण्ड प्रमेय के अनुसार g (x) = x + दिए गए बहुपद p (x) = 2x + 2 – 2x – 1 का एक गुणनखण्ड है।
(ii) p (x) = x3 + 3x2 + 3x + 1, g (x) = x + 2
हल:
प्रश्नानुसार p (x) = x3 + 3x2 + 3x + 1
तथाg (x) = x + 2
अब x + 2 = 0 या x = – 2
x = – 2 मान दिए गए p (x) में प्रतिस्थापित करने पर
p (-2) = (-2)3 + 3 (-2)2 + 3 (-2) + 1
= – 8 + 12 – 6 + 1
= – 14 + 13
= – 1 ≠ 0
अतः गुणनखण्ड प्रमेय के अनुसार g (x) = x + 2 दिए गए बहुपद p (x) = x3 + 3x2 + 3x + 1 का एक गुणनखण्ड नहीं है।
(iii)p (x) = x3 – 4x2 + x + 6, 8 (x) = x – 3
हल:
प्रश्नानुसार p (x) = x3 – 4x2 + x + 6 तथा
g (x) = x – 3 अब x – 3 = 0 या x = 3
x = 3 मान दिए गए p (x) में प्रतिस्थापित करने पर
p (3) = (3)3 – 4(3)2 + (3) + 6
= 27 – 36 + 3 + 6
= 36 – 36
= 0
अतः गुणनखण्ड प्रमेय के अनुसार g (x) = x – 3 दिए गए बहुपद p (x) = r – 4r + x + 6 का एक गुणनखण्ड है।
प्रश्न 3.
k का मान ज्ञात कीजिए जबकि निम्नलिखित स्थितियों में से प्रत्येक स्थिति में (x – 1), p (x) का एक गुणनखण्ड हो
(i) p (x) = x2 + x + k
हल:
प्रश्नानुसार (x – 1) बहुपद p (x) = + x + k का एक गुणनखण्ड है
अत: बहुपद में x = 1 रखने पर
p (1) = 0 होना चाहिए।
अर्थात् (1)2 + 1 + k = 0
1 + 1 + k = या
2 + k = 0
k = – 2
(ii) p (x) = 2x2 + kx + √2
हल:
प्रश्नानुसार (x – 1) बहुपद p (x) = 2x2 + kx + √2 का एक गुणनखण्ड है
अत: बहुपद में x = 1 रखने पर
p (1) = 0 होना चाहिए।
अर्थात् 2 (1)2 + k (1) + √2 = 0
या 2 + k + √2 = 0
या k= -(2 + √2)
(iii) p (x) = kx2 – √2x + 1
हल:
प्रश्नानुसार (x – 1) बहुपद p (x) = kx2 – √2x + 1 का एक गुणनखण्ड है अत: बहुपद में x = 1 रखने पर
p (1) = 0 होना चाहिए।
अर्थात् k (1)2 – √2 (1) + 1 = 0
या k – √2 + 1 = 0.
k = √2 – 1
(iv) p (x) = kx2 – 3x + k
हल:
प्रश्नानुसार (x – 1) बहुपद p (x) = kr – 3x + k का एक गुणनखण्ड है
अत: बहुपद में x = 1 रखने पर
p (1) = 0 होना चाहिए।
अर्थात् k(1)2 – 3 (1) + k = 0
k – 3 + k = 0
2k – 3 = 0
या k = 3/2
प्रश्न 4.
गुणनखण्ड ज्ञात कीजिए
(i) 12x2 – 7x + 1
हल:
12x2 – 7x + 1
यहाँ पर x का गुणांक = – 7
∴ दो संख्याओं का योग – 4 + (-3) लेना है।
और x का गुणांक x स्थिर पद = 12 × 1 = 12
∴ दो संख्याओं का गुणा – 4 × (-3) लेना है।
= 12x2 – 4x – 3x + 1
= 4x (3x – 1) – 1 (3x – 1)
= (3x – 1) (4x – 1)
(ii) 2x2 + 7x + 3
हल:
2x2 + 7x + 3
x का गुणांक = 7 = 1 + 6
का गुणांक x स्थिर पद = 2 × 3 = 6
∴ दो संख्याओं का गुणा 6 × 1 लेना है।
= 2x2 + 6x + x + 3
= 2r (x + 3) + 1 (x + 3)
= (x + 3) (2x + 1)
(iii) 6x2 + 5x – 6
हल:
6x2 + 5x – 6
यहाँ पर x का गुणांक = 5
का गुणांक – स्थिर पद = 6 × (-6) = – 36
∴ दो संख्याओं का योग 9 + (-4) = 5 लेना है।
और दो संख्याओं का गुणनफल 9 × (-4) = – 36 लेना है।
= 6x2 + 9x – 4x – 6
= 3x (2x + 3) – 2 (2x + 3)
= (2x + 3) (3x – 2)
(iv) 3x2 – x – 4
हल:
3x2 – x – 4
यहाँ पर x का गुणांक = – 1
x2 का गुणांक x स्थिर पद
3x (-4) = – 12
∴ दो संख्याओं का योग = – 4 + 3 = – 1
और दो संख्याओं का गुणनफल = -4 × 3 = – 12..
= 3x2 – 4x + 3x – 4
= x (3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
प्रश्न 5.
गुणनखण्ड ज्ञात कीजिए
(i) x3 – 2x2 – x + 2
हल:
माना कि p (x) = x3 – 2x2 – x + 2
दिए गए बहुपद के अचर पद 2 के समस्त 1 गुणनखण्ड क्रमशः + 1 तथा + 2 हैं। निरीक्षण द्वारा बहुपद में x = – 1 रखने पर
p (- 1) = (- 1)3 – 2 (- 1)2 – (- 1) + 2
= – 1 – 2 + 1 + 2
= 0
अर्थात् गुणनखण्ड प्रमेय के अनुसार (x + 1) दिए गए बहुपद का एक गुणनखण्ड है।
अब बहुपद p (x) को x + 1 से भाग देने पर
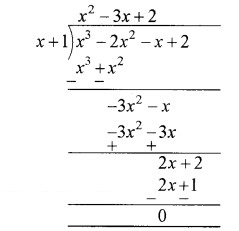
अतः x3 – 2x2 – x + 2 = (x + 1) (x2 – 3x + 2)
अब x2 – 3x + 2 के गुणनखण्ड करने के लिए मध्य पद को विभाजित कर या गुणनखण्ड प्रमेय का प्रयोग करने पर
अर्थात् x3 – 2x2 – x + 2
= (x + 1) (x2 – 3x + 2)
= (x + 1) [x2 – 2x – x + 2]
= (x + 1) [x (x – 2) – 1 (x – 2)]
= (x + 1) (x – 2) (x – 1)
= (x + 1) (x – 1) (x – 2)
(ii) x3 – 3x2 – 9x – 5
हल:
माना कि p (x) = x3 – 3x2 – 9x – 5
दिए गए बहुपद के अचर पद 5 के समस्त गुणनखण्ड क्रमशः + 1 तथा + 5 हैं।
निरीक्षण द्वारा बहुपद में x = – 1 रखने पर
p (- 1) = (- 1)3 – 3 (- 1)2 – 9(-1)-5
= – 1 – 3 + 9 – 5
= – 9 + 9 = 0
अर्थात् गुणनखण्ड प्रमेय के अनुसार (x + 1) दिए गए बहुपद का एक गुणनखण्ड है।
अब बहुपद p (x) को x + 1 से भाग देने पर
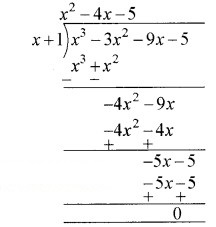
अत: x3 – 3x2 – 9x – 5 = (x + 1)(x2 – 4x – 5)
अब x2 – 4x – 5 के गुणनखण्ड करने के लिए मध्य पद को विभाजित कर या गुणनखण्ड प्रमेय का प्रयोग करने पर
अर्थात् x3 – 3x2 – 9x – 5
= (x + 1) (x2 – 4x – 5)
= (x + 1) [x2 – 5x + x – 5]
= (x + 1) [x (x – 5) + 1 (x – 5)]
= (x + 1) (x – 5) (x + 1)
= (x + 1) (x + 1) (x – 5)
(iii) x3 + 13x2 + 32x + 20
हल:
माना कि p (x) = x3 + 13x2 + 32x + 20
दिए गए बहुपद के अचर पद 20 के समस्त गुणनखण्ड क्रमशः + 1, + 2, + 4, + 5, + 10 तथा + 20 हैं।
निरीक्षण द्वारा बहुपद में x = – 1 रखने पर
p (- 1) = (-1)3 + 13 (-1)2 + 32 (-1) + 20
= – 1 + 13 – 32 + 20
= 33 – 33
= 0
अर्थात् गुणनखण्ड प्रमेय के अनुसार (x + 1) दिए गए बहुपद का एक गुणनखण्ड है।
अब बहुपद p (x) को x + 1 से भाग देने पर
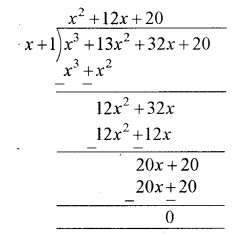
अत: x3 + 13x2 + 32x + 20 = (x + 1) (x2 + 12x + 20)
अब x2 + 12x + 20 के गुणनखण्ड ज्ञात करने के लिए मध्य पद को विभाजित कर या गुणनखण्ड प्रमेय का प्रयोग करने पर
अर्थात् x3 + 13x2 + 32x + 20
= (x + 1) (x2 + 12x + 20)
= (x + 1) [x2 + 10x + 2x + 20]
= (x + 1) [x (x + 10) + 2 (x+ 10)]
= (x + 1) (x + 10) (x + 2)
= (x + 1) (x + 2) (x + 10)
(iv) 2y3 + y2 – 2y – 1
हल:
माना कि p (y) = 2y3 + y2 – 2y – 1
दिए गए अचर पद 1 के समस्त गुणनखण्ड + 1 हैं।
निरीक्षण द्वारा बहुपद में y = 1 रखने पर
p (1) = 2 (1)3 + (1)2 – 2 (1) – 1
= 2 + 1 – 2 – 1
= 3 – 3 = 0
अर्थात् गुणनखण्ड प्रमेय के अनुसार (y – 1) दिए गए बहुपद का एक गुणनखण्ड है।
अब बहुपद p (y) को y – 1 से भाग देने पर
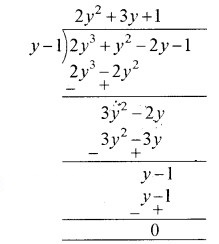
अत: 2y3 + y2 – 2y – 1 = (y – 1) (2y2 + 3y + 1)
अब 2y2 + 3y + 1 के गुणनखण्ड ज्ञात करने के लिए मध्यपद को विभाजित कर या गुणनखण्ड प्रमेय का प्रयोग करने पर
अर्थात् 2y3 + y2 – 2y – 1
= (y – 1) (2y2 + 3y + 1)
= (y – 1) [2y2 + 2 + y + 1]
= (y – 1) [27 (y + 1) + 1 (y + 1)]
= (y – 1) (y + 1) (2) + 1)