Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
Question 1.
Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting)? Represent this situation algebraically and graphically.
Solution:
Let present age of Aftab = x years and present age of Aftab’s daughter = y years.
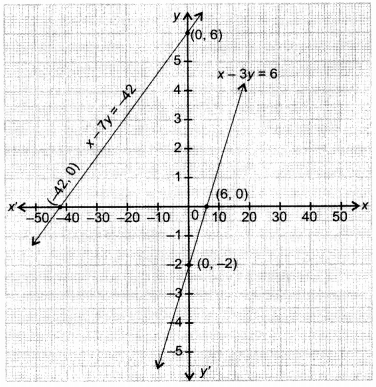
1st Condition :
Seven years ago
x – 7 = 7(y – 7)
⇒ x – 7 = 7y – 49
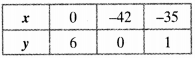
⇒ x – 7y = – 42
Table :
2nd Condition :
Three years later,
x + 3 = 3(y + 3)
x + 3 = 3y + 9
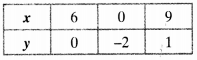
x – 3y = 6
Table :
Thus, the algebraic equations are
x – 7y + 42 = 0 and x – 3y – 6 = 0
Question 2.
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹ 1300. Represent this situation algebraically and geometrically.
Solution:
Let cost of one bat = ₹ x
and the cost of one ball = ₹y
A.T.Q.
1st Condition :
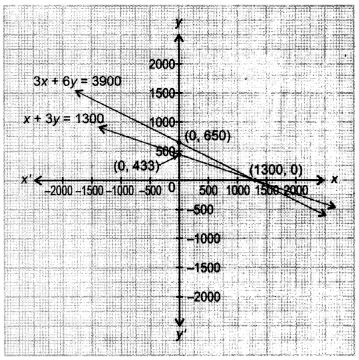
3x + 6y = 3900
Table :
2nd Condition :
x + 3y = 1300
Table :
Thus, the algebraic equations are 3x + 6y = 3900 and x + 3y – 1300
Question 3.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹ 300. Represent the situation algebraically and geometrically.
Solution:
Let cost of one kg of apples = ₹ x and the cost of one kg of grapes = ₹y
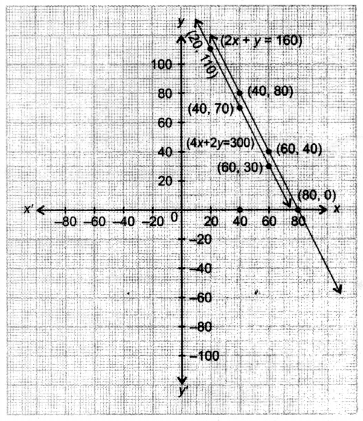
A.T.Q.
1st Condition :
2x + y = 160
Table :
2nd Condition :
4x + 2y = 300
Table :
Thus, algebraic situations are 2x + y = 160 and 4x + 2y = 300