Chapter 4 द्विघात समीकरण Ex 4.4
प्रश्न 1.
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का अस्तित्व हो, तो उन्हें ज्ञात कीजिए :
(i) 2x2 – 3x + 5 = 0
हल-
प्रश्नानुसार
2x2 – 3x + 5 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 2, b = -3, c = 5
विविक्तकर (D) = b2 – 4ac
= (-3)2 – 4 × 2 × 5
= 9 – 40
= -31 < 0
अतः दी गयी द्विघात समीकरण का कोई वास्तविक मूल नहीं है।
(ii) 3x2 – 4√3x + 4 = 0
हल-
प्रश्नानुसार 3x2 – 4√3x + 4 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 3, b = -4√3, c = 4
विविक्तकर (D) = b2 – 4ac
= (-4√3)2 – 4 × 3 × 4
= 48 – 48
= 0
अतः दी गई समीकरण के वास्तविक और बराबर मूल हैं।
अब,
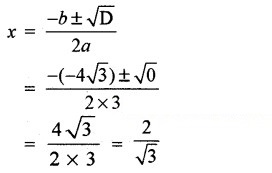
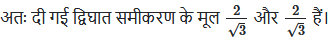
(iii) 2x2 – 6x + 3 = 0
हल-
प्रश्नानुसार
2x2 – 6x + 3 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 2, b = -6, c = 3
विविक्तकर (D) = b2 – 4ac
= (-6)2 – 4 × 2 × 3
= 36 – 24
= 12 > 0
∵ दी गई द्विघात समीकरण के वास्तविक और भिन्न मूल हैं।
अब,
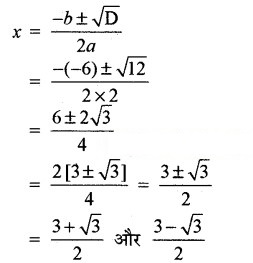
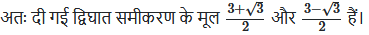
प्रश्न 2.
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों।
(i) 2x2 + kx + 3 = 0
हल-
प्रश्नानुसार
2x2 + kx + 3 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 2, b = k, c = 3
∵ दी गई द्विघात समीकरण के मूल बराबर हैं।
∴ विविक्तकर (D) = 0
b2 – 4ac = 0
या (k)2 – 4 × 2 × 3 = 0
या k2 – 24 = 0
या k2 = 24
या k = ±√24
या k = ±2√6
अतः मूल बराबर होने के लिये k = ±2√6 होना चाहिये।
(ii) kx(x – 2) + 6 = 0
हल-
प्रश्नानुसार kx(x – 2) + 6 = 0
या kx2 – 2kx + 6 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = k, b = -2k, c = 6
∵ दी गई द्विघात समीकरण के मूल बराबर हैं।
D = 0
या b2 – 4ac = 0
या (-2k)2 – 4 × k × 6 = 0
या 4k2 – 24k = 0
या 4k[k – 6] = 0
अर्थात् 4k = 0 या k – 6 = 0
k = 0 या k = 6
k = 0 द्विघात समीकरण में रखने पर 6 = 0 प्राप्त होता है जो कि असम्भव है।
अतः k का सही मान k = 6 ही है।
प्रश्न 3.
क्या एक ऐसी आम की बगिया बनाना सम्भव है जिसकी लम्बाई, चौड़ाई से दुगुनी हो और उसका क्षेत्रफल 800 m2 हो? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल-
माना कि आयताकार बगिया की लम्बाई = x m
और आयताकार बगिया की चौड़ाई = 2x m
आयताकार बगिया का क्षेत्रफल = लम्बाई × चौड़ाई
= [x × 2x] m2
= 2x2 m2
प्रश्नानुसार
2x2 = 800
x2 = 400
x = ±√400
x = ±20
∵ आयताकार की लम्बाई ऋणात्मक नहीं हो सकती।
इसलिए x = -20 को छोड़ने पर
∴ x = 20
यहाँ पर x का मान वास्तविक प्राप्त हुआ है।
इस कारण से ऐसी आम की बगिया बनाना सम्भव है।
∴ आयताकार बगिया की चौड़ाई = 20 m
और आयताकार बगिया की लम्बाई = (2 × 20) m = 40 m
प्रश्न 4.
क्या निम्न स्थिति सम्भव है? यदि है तो उनकी वर्तमान आयु ज्ञात कीजिए। दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु (वर्षों में) का गुणनफल 48 था।
हल-
माना कि पहले मित्र की आयु = x वर्ष
और दूसरे मित्र की आयु = (20 – x) वर्ष
चार वर्ष पूर्व,
पहले मित्र की आयु = (x – 4) वर्ष
और दूसरे मित्र की आयु = (20 – x – 4) वर्ष = (16 – x) वर्ष
∴ उनका गुणनफल = (x – 4) (16 – x)
= 16x – x2 – 64 + 4x
= -x2 + 20x – 64
प्रश्नानुसार
-x2 + 20x – 64 = 48
या -x2 + 20x – 64 – 48 = 0
या -x2 + 20x – 112 = 0
या x2 – 20x + 112 = 0 ……(1)
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -20, c = 112
विविक्तकर (D) = b2 – 4ac
= (-20)2 – 4 × 1 × 112
= 400 – 448
= -48 < 0
∵ मूल वास्तविक नहीं है।
इसलिए, x का कोई मान द्विघात समीकरण (1) को सन्तुष्ट नहीं कर सकता।
अतः दी गई स्थिति सम्भव नहीं है।
प्रश्न 5.
क्या परिमाप 80 m तथा क्षेत्रफल 400 m2 के |एक पार्क को बनाना सम्भव है? यदि है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए।
हल-
माना कि
आयताकार पार्क की लम्बाई = x m
आयताकार पार्क की चौड़ाई = y m
∴ आयताकार पार्क का परिमाप = 2(x + y) m
और आयताकार पार्क का क्षेत्रफल = xy m2
पहली शर्त के अनुसार,
2(x + y) = 80
x + y = 40
y = 40 – x …..(1)
दूसरी शर्त के अनुसार,
xy = 400
x(40 – x) = 400 [∵ (1) का प्रयोग करने पर]
40x – x2 = 400
या 40x – x2 – 400 = 0
x2 – 40x + 400 = 0
इसकी तुलना ax2 + bx + c = 0 से करने पर,
∴ a = 1, b = -40, c = 400
विविक्तकर (D) = b2 – 4ac
= (-40)2 – 4 × 1 × 400
= 1600 – 1600
= 0
अतः इस द्विघात समीकरण के मूल वास्तविक और बराबर होंगे।
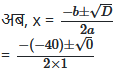
= 20
जब x = 20, तो (1) से y = 40 – 20 = 20
∴ आयताकार पार्क की लम्बाई और चौड़ाई का माप 20 m के बराबर है।
अतः दी गई आयताकार पार्क का अस्तित्व सम्भव है और यह एक वर्ग है।