Chapter 5 युक्लिड के ज्यामिति का परिचय Ex 5.1
प्रश्न 1.
निम्नलिखित कथनों में से कौन-से कथन सत्य हैं और कौन-से कथन असत्य हैं ? अपने उत्तरों के लिए कारण दीजिए-
(i) एक बिन्दु से होकर केवल एक ही रेखा खींची जा सकती है।
(ii) दो भिन्न बिन्दुओं से होकर जाने वाली असंख्य रेखाएँ हैं।
(iii) एक सांत रेखा दोनों ओर अनिश्चित रूप से बढ़ाई जा सकती है।
(iv) यदि दो वृत्त बराबर हैं, तो उनकी त्रिज्याएँ बराबर होती हैं।
(v) आकृति में, यदि AB = PQ और PQ = XY है, तो AB = XY होगा।
हल:
(i) यह कथन असत्य है क्योंकि यह स्वयंसिद्ध है कि एक बिन्दु से होकर असीमित रूप से अनेक रेखाएँ खींची जा सकती हैं। यह हम आगे बनी आकृति के द्वारा भी देख सकते हैं।
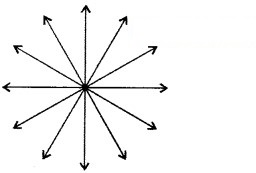
(ii) यह कथन असत्य है क्योंकि दिया गया यह कथन यूक्लिड के अभिगृहीत 1 का विरोधाभासी कथन है क्योंकि इस कथन में कहा गया है कि “दिए हुए दो भिन्न बिन्दुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
![]()
उपर्युक्त चित्र के अनुसार हम देख सकते हैं कि दो बिन्दुओंA तथा B में से एक अद्वितीय रेखा खींची जा सकती है।
(iii) यह कथन सत्य है। यूक्लिड की अभिधारणा 2 के अनुसार “एक सांत रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।” जैसा कि निम्न चित्र में दिखाया गया है कि रेखा RS को अनिश्चित रूप से बढ़ाया जा सकता है।
![]()
(iv) प्रश्न में दिया गया यह कथन सत्य है। यूक्लिड की अभिगृहीत 4 के अनुसार, “वे वस्तुएँ जो परस्पर संपाती हों, एक-दूसरे के बराबर होती हैं।” प्रश्न के कथन में दिए अनुसार वृत्त आपस में बराबर हैं। यदि एक वृत्त को दूसरे वृत्त पर अध्यारोपित करें तो वे संपाती होंगे। अतः इनके केन्द्र तथा परिधि अर्थात् परिसीमाएँ संपाती होंगी। इससे यह भी प्रमाणित होता है कि इन वृत्तों की त्रिज्याएँ भी बराबर होंगी।
(v) यह कथन सत्य है। यूक्लिड की अभिगृहीत 1 के अनुसार “वे वस्तुएँ जो एक ही वस्तु के बराबर हों, एक-दूसरे के बराबर होती हैं।”
प्रश्न 2.
निम्नलिखित पदों में से प्रत्येक की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएंगे?
(i) समान्तर रेखाएँ
(ii) लम्ब रेखाएँ
(iii) रेखाखण्ड
(iv) वृत्त की त्रिज्या
(v) वर्ग।
हल:
(i) समान्तर रेखाएँ-समान्तर रेखाएँ वे सीधी एवं सरल रेखाएँ होती हैं जो एक तल में होती हैं तथा दोनों दिशाओं में असीमित लम्बाई तक बढ़ाने पर भी कभी भी आपस में नहीं मिलती हैं। जैसा कि निम्नांकित चित्र में रेखा l व m को दर्शाया गया है-
![]()
समान्तर रेखाओं को l || m द्वारा लिखा जाता है।
समान्तर रेखाओं को परिभाषित करने पर पद समतल आता है। यह एक अपरिभाषित पद है। इस पद को अन्तःप्रेरणा से ही समझा जा सकता है जैसे चिकनी दीवार की सतह, एक बड़े कागज की सतह, श्यामपट्ट का चिकना तल आदि। कल्पना यह करनी पड़ती है कि सतह को उसके आयाम के अनुसार असीमित सीमाओं तक बढ़ाया जा सकता है।
(ii) लम्ब रेखाएँ-यदि एक सरल रेखा किसी अन्य सरल रेखा पर इस प्रकार मिले कि बनने वाले आसन्न कोण आपस में बराबर या समान हों तो बनने वाला प्रत्येक कोण समकोण होगा तथा सरल रेखा जो अन्य रेखा पर मिल रही है, उस पर लम्ब रेखा कहलाती है। इससे सम्बन्धित कुछ अन्य पद निम्नलिखित हैं-
(A) कोण-कोई भी दो किरणें जिनका प्रारम्भिक बिन्दु एक ही हो, कोण बनाती हैं अर्थात् इसे इस तरह भी परिभाषित किया जा सकता है कि यदि किसी एक बिन्दु से दो 0 किरणें निकलें तो बनने वाली आकृति कोण कहलाएगी।


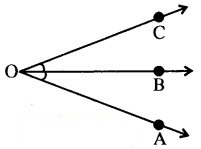
(B) आसन्न कोण-ऐसे दो कोण जिनका शीर्ष एवं एक 06 भुजा उभयनिष्ठ हो, आसन्न कोण कहलाते हैं। सामने चित्र में ∠AOB तथा ∠COB आसन्न कोण हैं। इनमें शीर्ष 0 एवं भुजा OB उभयनिष्ठ है।
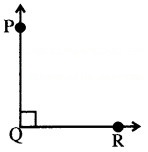
(C) समकोण-ऐसा 4 कोण जिसका माप 90° के PP बराबर हो, समकोण कहलाता है। या यह भी कहा जा सकता है कि एक ऐसा कोण जो एक बिन्दु पर बनने वाले सम्पूर्ण d कोणों के योग का चौथाई हो, समकोण कहलाता है।
(iii) रेखाखण्ड-एक ऐसी आकृति जिसकी लम्बाई सीमित हो, तथा यदि चाहें तो उसे दोनों ओर असीमित लम्बाई तक बढ़ाया जा सके, रेखाखण्ड कहलाती है। इससे सम्बन्धित अन्य पद रेखा है जिसे परिभाषित करने की आवश्यकता है।
![]()


(iv) वृत्त की त्रिज्या-किसी बिन्दु से वृत्त की परिधि तक की स्थिर दूरी को वृत्त की त्रिज्या कहते हैं। अर्थात् एक ऐसा रेखाखण्ड जो वृत्त की परिधि के किसी भी बिन्दु को केन्द्र से मिलाता है, वृत्त की त्रिज्या कहलाता है। इससे सम्बन्धित निम्नलिखित पदों को परिभाषित करने की आवश्यकता है-
(A) वृत्त-एक तल पर उन सभी बिन्दुओं का समूह, जो तल के एक स्थिर बिन्दु से एक स्थिर दूरी पर स्थित हों, एक वृत्त कहलाता है। .
(B) वृत्त का केन्द्र-किसी भी वृत्त का वह स्थिर बिन्दु जिससे वृत्त पर स्थित समस्त बिन्दु एकसमान दूरी पर हों, वृत्त का केन्द्र कहलाता है।
(v) वर्ग-ऐसी चतुर्भुजाकार आकृति जिसमें समस्त भुजाएँ एवं समस्त कोण समान हों, वर्ग कहलाती है। किसी भी वर्ग में-
(a) चारों भुजाएँ बराबर होती हैं।
(b) प्रत्येक कोण समकोण होता है।
(c) विकर्ण बराबर होते हैं।
(d) विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।
(e) प्रत्येक विकर्ण भुजा के साथ 45° का कोण बनाता है।
प्रश्न 3.
नीचे दी हुई दो अभिधारणाओं पर विचार कीजिए
(i) दो भिन्न बिन्दु A और B दिए रहने पर, एक तीसरा बिन्दु C ऐसा विद्यमान है जो A और B के बीच स्थित होता है।
(ii) यहाँ कम से कम ऐसे तीन बिन्दु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं।
क्या इन अभिधारणाओं में कोई अपरिभाषित शब्द हैं? क्या ये अभिधारणाएँ अविरोधी हैं? क्या ये यूक्लिड की अभिधारणाओं से प्राप्त होती हैं? स्पष्ट कीजिए।
हल:
उपर्युक्त प्रश्न में दी गई अभिधारणाओं में एक अपरिभाषित शब्द बिन्दु है जिसकी छात्र को जानकारी होनी चाहिए। बिन्दु के अतिरिक्त रेखा भी अपरिभाषित शब्द है किन्तु पिछले प्रश्न में इसका वर्णन कर दिया है।
बिन्दु:
बिन्दु की संकल्पना को निम्नलिखित उपकरणों द्वारा समझा जा सकता है। एक बारीक पेन्सिल द्वारा लगाया गया सूक्ष्म चिह्न, श्यामपट्ट का कोना एक बिन्दु के मिलते-जुलते उदाहरण हैं। पेन्सिल का कोना जितना अधिक बारीक होगा, उस द्वारा बनाया गया चिह्न उतना ही अच्छा बिन्दु होता है। साधारणतः बिन्दु को अंग्रेजी वर्णमाला के बड़े अक्षरों अर्थात् A, B, C, D आदि द्वारा दर्शाया जाता है।
प्रश्न में दी गई दोनों अभिधारणाएँ (i) तथा (ii) संगत हैं क्योंकि इनमें दो अलग-अलग स्थितियों का अध्ययन किया जाता है। अभिधारणा (i) में कथन दिया है कि यदि दो बिन्दु A और B दिए हुए हों, तो उनके बीच में एक बिन्दु C होता है जिसे निम्न प्रकार दर्शाया जा सकता है-
![]()
अभिधारणा (ii) का कथन है कि यहाँ कम से कम तीन ऐसे बिन्दु विद्यमान हैं कि वे एक रेखा पर स्थित नहीं हैं। इसके लिए दो दिए हुए बिन्दुओं A और B के लिए हम एक बिन्दु C ले सकते हैं जो A तथा B से होकर जाने वाली रेखा पर स्थित नहीं होता।
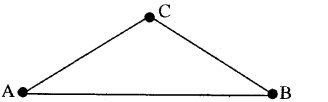
इस प्रकार हम देखते हैं कि ये दोनों अभिगृहीत यूक्लिड की अभिगृहीतों का अनुसरण नहीं करते। फिर भी ये अभिंगृहीत 5.1 का अनुसरण करते हैं। इस अभिगृहीत के अनुसार दिए गए दो बिन्दुओं के लिए भिन्न एक अद्वितीय रेखा होती है जो उनमें से होकर जाती है।
प्रश्न 4.
यदि दो बिन्दुओं A और B के बीच एक बिन्दु C ऐसा स्थित है कि AC = BC है, तो सिद्ध कीजिए कि AC = 1/2AB है। एक आकृति खींच कर इसे स्पष्ट कीजिए।
हल:
प्रश्नानुसार दिया गया है कि बिन्दु C, बिन्दु A व B के बीच स्थित है। तभी AC = BC हो सकता है।
![]()
दोनों पक्षों में AC जोड़ने पर
AC + AC = AC + BC
यहाँ यूक्लिड की परिभाषा के अनुसार बराबरों को बराबरों में जोड़ा गया है।
अतः 2AC = AB
[∵ BC + AC, AB के संपाती हैं।]
![]()
प्रश्न 5.
प्रश्न 4 में, C रेखाखण्ड AB का एक मध्य-बिन्दु कहलाता है। सिद्ध कीजिए कि एक रेखाखण्ड का एक और केवल एक ही मध्य-बिन्दु होता है।
हल:
माना AB का D एक और मध्य बिन्दु है।
∴ AD = DB …….. (i)
लेकिन दिया गया है कि C, AB का मध्य बिन्दु है।
AC = CB ……… (ii)
(i) को (ii) में से घटाने पर
AC – AD = CB – DB
या DC = – DC
या DC + DC = 0
या 2DC = 0
या DC = 0
अतः C व D सम्पाती हैं।
इसलिए हर एक रेखाखण्ड का केवल एक ही मध्य बिन्दु होता है। (इति सिद्धम्)
प्रश्न 6.
आकृति में यदि AC = BD है, तो सिद्ध कीजिए कि AB = CD है।
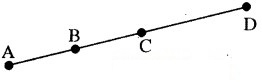
हल:
प्रश्नानुसार AC = BD (दिया है) …..(i)
या AC = AB + BC …..(ii)
[∵ बिन्दु B, बिन्दुओं A और C के बीच स्थित है]
या BD = BC + CD …..(iii)
[∵ बिन्दु C, B और D के बीच स्थित है।]
समीकरण (ii) व (iii) का मान (i) में प्रतिस्थापित करने पर
AB + BC = BC + CD
दोनों पक्षों में BC घटाने पर
AB + BC – BC = BC + CD – BC
= BC – BC + CD
या AB = CD
यूक्लिड की अभिगृहीत बराबरों में से बराबरों को घटाने पर शेषफल भी बराबर होता है। (इति सिद्धम्)
प्रश्न 7.
यूक्लिड की अभिगृहीतों की सूची में दिया गया अभिगृहीत 5 एक सर्वव्यापी सत्य क्यों माना जाता है ? (ध्यान दीजिए कि यह प्रश्न पाँचवीं अभिधारणा से सम्बन्धित नहीं है।)
हल:
यूक्लिड की अभिगृहीत 5 के अनुसार, “एक पूर्ण अपने भाग से बड़ा होता है।” इस अभिगृहीत को एक सर्वव्यापी सत्य इसलिए माना जाता है क्योंकि विश्व के किसी भाग में किसी भी वस्तु के लिए यह सत्य होता है।