Chapter 6 त्रिभुज और उसके गुण Ex 6.3
प्रश्न 1.
निम्नांकित आकृतियों में अज्ञात x का मान ज्ञात कीजिए –
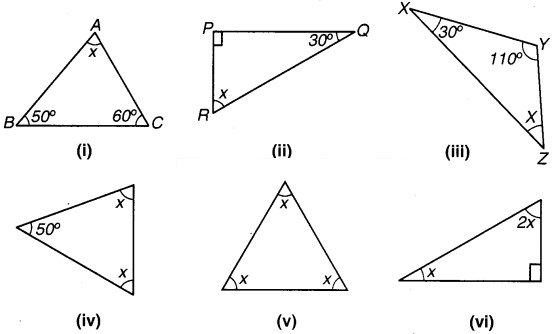
हल:
∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° (दो समकोण) के बराबर होता है। अतः
(i) x+ 50° + 60° = 180°
या x + 110° = 180°
या x = 180° – 110° = 700
अतः x का अभीष्ट मान = 70°
(ii) x + 90° + 30° = 180°
या x + 120° = 180°
या x = 180° – 120° = 60°
अतः का अभीष्ट मान = 60°
(iii) x + 30° + 110° = 180°
या x + 140° = 180°
या x = 180° – 140° = 40°
अत: x का अभीष्ट मान = 40°
(iv) x + x + 50 = 180°
या 2x + 50° = 180°
या 2x = 180° – 50° = 130°
या x = = 60°
अतः x का अभीष्ट मान = 65°
(v) x + x + x = 180°
या 3x = 180°
या x = = 60°
अतः x का अभीष्ट मान = 60°
(vi) x + 2x + 90° = 180°
या 3x = 180° – 90° = 90°
या x = = 30°
अतः x का अभीष्ट मान = 30°
प्रश्न 2.
निम्नांकित आकृतियों में अज्ञात x और y का मान ज्ञात कीजिए –
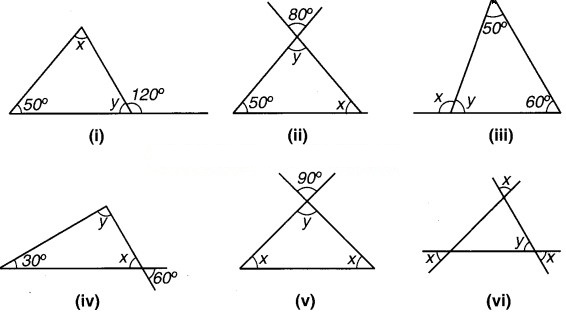
हल:
(i) ∵ कोण y और 120° रैखिक युग्म बनाते हैं।
∴ y + 120° = 180°
या y = 180° – 120° = 60°
(∵ त्रिभुज के तीनों अन्तः कोणों का योग = 180°)
अब x + y + 50° = 180°
या x + 60° + 50° = 180°
या x + 110° = 180°
या x = 180° – 110° = 70°
अतः x = 70° और y = 60°
(ii) ∵ कोण y और 80° ऊर्ध्वाधर सम्मुख कोण हैं,
∴ y = 80°
∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° होता है।
∴ x + y + 50° = 180°
या x + 80° + 50° = 180°
या x + 130° = 180°
या x = 180° – 130° = 50°
अत: x = 50° और y = 80°
(iii) ∵ त्रिभुज के तीनों अन्तः कोणों का योग = 180°
∴ 50° + 60° + y = 180°
या 110° + y = 180°
या y = 180° – 110° = 70°
पुनः कोण x और y रैखिक युग्म बनाते हैं
∴ x + y = 180°
या x + 70° = 180°
या x = 180° – 70° = 110°
अतः x = 110° और y = 70°
(iv) ∵ कोण x और 60° ऊर्ध्वाधर सम्मुख कोण हैं।
∴ x = 60°
अब, ∵ त्रिभुज के तीनों अन्त:कोणों का योग 180° होता है।
∴ x + 1 + 30° = 180°
या 60 + 1 + 30° = 180°
या y + 90° = 180°
या y = 180° – 90° = 90°
अतः x = 60° और y = 90°
(v) ∵ कोण । और 90° ऊर्ध्वाधर सम्मुख कोण हैं,
∴ y = 90°
अब, ∵ त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + y = 180°
या 2x + 90° = 180°
या 2x = 180° – 90°
= 90°
⇒ x = =45°
अतः x = 45° और y = 90°
(vi) त्रिभुज का एक अन्त:कोण y है। शेष दो कोण ऊर्ध्वाधर सम्मुख कोण x के बराबर हैं।
∴ x + x + y = 180°
या 2x + y = 180°
या 2x + x = 180° (∵ ∠x = ∠y)
या 3x = 180°
या x = = 60°
अतः x = 60° और y = 60°
पाठ्य-पुस्तक पृष्ठ संख्या # 184
प्रयास कीजिए
प्रश्न 1.
एक त्रिभुज के दो कोण 30° तथा 80° हैं। इस त्रिभुज का तीसरा कोण ज्ञात कीजिए।
हल:
माना कि तीसरा कोण x है,
∵ त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ 30° + 80° + x = 180°
या 110° + x = 180°
या x = 180° – 110° = 70°
अतः त्रिभुज का तीसरा कोण = 70°
प्रश्न 2.
किसी त्रिभुज का एक कोण 80° तथा शेष दोनों कोण बराबर हैं। बराबर कोणों में प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
माना कि बराबर कोणों में प्रत्येक कोण x है।
∵ त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
∴ x + x + 80° = 180°
या 2x + 80° = 180°
या 2x = 180° – 80° = 100°
या x = = 50°
अत: बराबर कोणों में प्रत्येक कोण = 50°
प्रश्न 3.
किन्हीं त्रिभुज के तीनों कोणों में 1 : 2 : 1 का अनुपात है। त्रिभुज के तीनों कोण ज्ञात कीजिए। त्रिभुज का दोनों प्रकार से वर्गीकरण भी कीजिए।
हल:
माना कि त्रिभुज के कोण x, 2x व x हैं।
∴ x + 2x + x = 180°
या 4x = 180°
या x = = 45°
त्रिभुज के कोण x = 45° तथा 2x = 2 × 45° = 90°
अत: त्रिभुज के कोण 45°, 90° और 45° हैं।
अतः त्रिभुज समकोण त्रिभुज है तथा यह समद्विबाहु त्रिभुज भी है।
सोचिए, चर्चा कीजिए एवं लिखिए
प्रश्न 1.
क्या कोई ऐसा त्रिभुज सम्भव है जिसके दो कोण समकोण हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं हैं जिसके दो कोण समकोण हों क्योंकि त्रिभुज के तीनों अन्तः कोणों का योग 180° होता है।
प्रश्न 2.
क्या कोई ऐसा त्रिभुज सम्भव नहीं है जिसमें दो | कोण अधिक कोण हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है, जिसमें दो कोण अधिक कोण हों। यहाँ इस स्थिति में त्रिभुज के तीनों कोणों का योग दो समकोण से अधिक हो जाएगा।
प्रश्न 3.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें दो – कोण न्यून कोण हों ?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें दो न्यून कोण हों।
प्रश्न 4.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° से अधिक हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें सभी तीनों कोण 60° से अधिक हों। इस स्थिति में त्रिभुज के तीनों कोणों का योग 180° से अधिक हो जाएगा, लेकिन यह 180° के बराबर होना चाहिए।
प्रश्न 5.
क्या कोई ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हो ?
हल:
हाँ, ऐसा त्रिभुज सम्भव है जिसमें तीनों कोण 60° के हों।
प्रश्न 6.
क्या कोई ऐसा त्रिभुज सम्भव है। जिसमें तीनों कोण 60° से कम हों ?
हल:
नहीं, ऐसा त्रिभुज सम्भव नहीं है जिसमें तीनों कोण 60° से कम हों। ऐसी स्थिति में त्रिभुज के तीनों कोणों का योग 180° से कम होगा जबकि यह 180° होना चाहिए।
पाठ्य-पुस्तक पृष्ठ संख्या # 135-136
प्रयास कीजिए
प्रश्न 1.
प्रत्येक आकृति में कोण x का मान ज्ञात कीजिए –
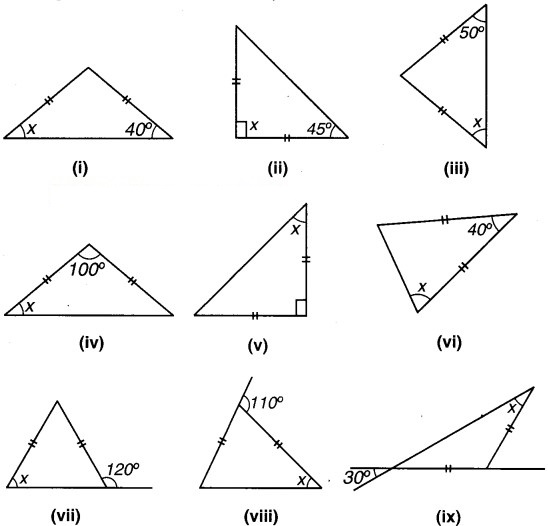
हल:
(i) आकृति समद्विबाहु त्रिभुज है जिसमें दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
∴ अभीष्ट कोण x = 40°
(ii) आकृति समकोण समद्विबाहु त्रिभुज है, जिसकी दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
अतः दूसरी समान भुजा के सामने का कोण 45° है।
चूँकि हम जानते हैं कि त्रिभुज के तीनों कोणों का योग 180° होता है। अतः
x + 45° + 45° = 180°
या x + 90° = 180°
या x = 180° – 90° = 90°
∴ अभीष्ट कोण x = 90°
(iii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं,
∴ अभीष्ट कोण x = 50°
(iv) आकृति में त्रिभुज की दो भुजाएँ समान हैं और समान भुजाओं के सामने के कोण समान होते हैं।
∴ आधार का दूसरा कोण = x.
अब, त्रिभुज के तीनों कोणों का योग = 180°
∴ x + x + 100° = 180°
या 2x + 100° = 180°
या 2x = 180° – 100°
= 80°
∴ अभीष्ट कोण x = = 40°
(v) आकृति में दो भुजाएँ समान हैं तथा एक कोण समकोण है और समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा कोण = x
∵ त्रिभुज के तीनों अन्त: कोणों का योग = 180°
∴ x + x + 90° = 180°
या 2x = 180° – 90° = 90°
∴ अभीष्ट कोण x = = 45°
(vi) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा कोण भी x होगा।
∵ त्रिभुज के तीनों कोणों का योग = 180°
∴ x + x + 40° = 180°
या 2x + 40° = 180°
या 2x = 180° – 40° = 140°
∴ अभीष्ट कोण x = = 70°
(vii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
∵ दूसरा आधार कोण x और 120° रैखिक युग्म बनाते हैं।
∴ x + 120° = 180°
∴ अभीष्ट कोण x = 180° – 120°
= 60°
(viii) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
चूँकि सम्मुख अत: कोणों का योग = बाह्य कोण
∴ x + x = 110°
या 2x = 110°
∴ अभीष्ट कोण x = = 55°
(ix) आकृति में त्रिभुज की दो भुजाएँ समान हैं और त्रिभुज में समान भुजाओं के सामने के कोण समान होते हैं।
∴ दूसरा आधार का कोण = x
साथ ही, ऊर्ध्वाधर सम्मुख कोण x और 30° बराबर हैं।
∴ अभीष्ट कोण x = 30°
प्रश्न 2.
प्रत्येक आकृति में x तथा y के मान ज्ञात कीजिए –
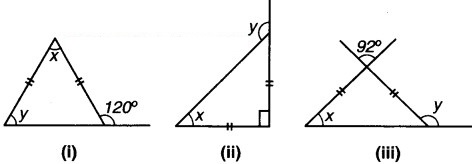
हल:
(i) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
चूँकि एक आधार का कोण = y
∴ दूसरा आधार का कोण = y
अब, दूसरा आधार कोण y और 120° रैखिक युग्म बनाते हैं।
∴ y + 120° = 180°
या y = 180° – 120° = 60°
अब, त्रिभुज के तीनों अन्तः कोणों का योग = 180°
∴ x + y + y = 180°
या x + 2y = 180°
या x + 2 × 60° = 180°
या x = 180° – 120° = 60
अतः, x = 60° और y = 60°
(ii) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
∵ समान कोणों में एक कोण x है, अतः दूसरा कोण = x साथ ही, त्रिभुज समकोण त्रिभुज है
∴ तीसरा कोण = 90°
अब, त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + 90° = 180°
या 2x + 90° = 180°
या 2x = 180° – 90° = 90°
या x = = 45°
अब, दूसरा कोण x और रैखिक युग्म बनाते हैं।
∴ x + y = 180°
या 45° + y = 180°
∴ y = 180° – 45° = 135°
अतः x = 45° और y = 135°
(iii) आकृति में त्रिभुज की दो भुजाएँ समान हैं।
∴ समान भुजाओं के सामने के कोण समान हैं।
समान कोण में एक कोण x है।
अतः दूसरा आधार कोण = x
त्रिभुज का तीसरा कोण = ऊर्ध्वाधर सम्मुख कोण
= 92°
अब, त्रिभुज के तीनों अन्त:कोणों का योग = 180°
∴ x + x + 92° = 180°
या 2x + 92° = 180°
या 2x = 180° – 92° = 88°
या x = = 44°
अब, दूसरा आधार कोण x और y रैखिक युग्म बनाते हैं।
∴ x + y = 180°
या 44° + y = 180°
या y = 180° – 44° = 136°
अतः x = 44° और y = 136°
पाठ्य-पुस्तक पृष्ठ संख्या # 137
प्रश्न 1.
अपनी अभ्यास-पुस्तिका में कोई तीन त्रिभुज, जैसे – ∆ABC, ∆PQR और ∆XYZ बनाइए। अपने पैमाने की सहायता से इन त्रिभुजों की भुजाओं को मापकर, एक तालिका के रूप में निम्न प्रकार से लिखिए
हल:
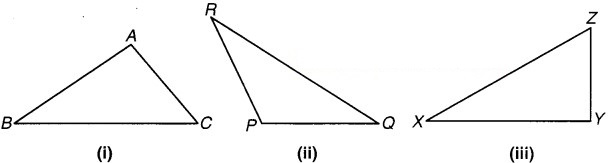
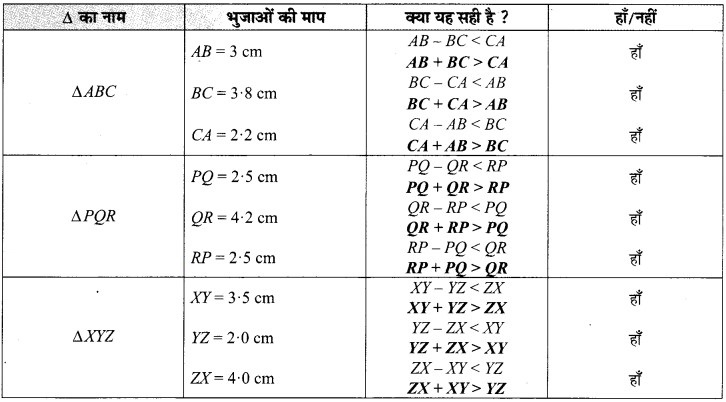
पाठ्य-पुस्तक पृष्ठ संख्या # 138-139