Chapter 7 त्रिभुज Ex 7.3
प्रश्न 1.
∆ABC और ∆DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे तो दर्शाइए कि
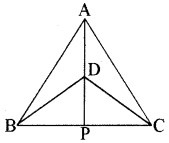
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP कोण A और कोण D दोनों को समद्विभाजित करता है।।
(iv) AP रेखाखण्ड BC का लम्ब समद्विभाजक
हल:
(i) प्रश्न में दिए अनुसार ∆ABC एक समद्विबाहु त्रिभुज है।
अतः AB = AC
इसी प्रकार दूसरा ∆DBC एक समद्विबाहु त्रिभुज है। अतः
BD = CD
अब ∆ABD तथा ∆ACD में
AB = AC (दिया है)
BD = CD (दिया है)
तथा AD = AD (उभयनिष्ठ)
∴ ∆ABD ≅ ∆ACD
[सर्वांगसमता के SSS नियम के अनुसार]
अतः ∠BAD = ∠CAD …..(i) [क्योंकि ये सर्वांगसम त्रिभुज के संगत भाग हैं]
(ii) अब ∆ABD और ∆ACD में
AB = AC (दिया है)
∠BAD = ∠CAD
[समीकरण (i) के अनुसार]
तथा AP = AP (उभयनिष्ठ भुजाएँ)
∴ ∆ABP = ∆ACP
[सर्वांगसमता के नियम SAS के अनुसार
(iii) इस प्रश्न के द्वितीय भाग में सिद्ध किया है
∆ABP ≅ ∆ACP
अतः ∠BAP = ∠CAP [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं]
अतः AP, ∠A को समद्विभाजित करता है।
भाग (i) के अनुसार
∆ABD ≅ ∆ACD
अतः ∠ADB = ∠ADC …..(ii) [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं]
तथा ∠ADB + ∠BDP = 180° …..(iii)
(रैखिक युग्म अभिगृहीत से)
तथा ∠ADC + ∠CDP = 180° …..(iv)
(रैखिक युग्म अभिगृहीत से)
अब समीकरण (iii) व (iv) से
या ∠ADB + ∠BDP = ∠ADC + ∠CDP
या ∠ADB + ∠BDP = ∠ADB + ∠CDP [समीकरण (ii) के अनुसार]
∠BDP = ∠CDP
अर्थात् DP, ∠D को समद्विभाजित करता है।
यह कहा जा सकता है कि AP कोण A तथा कोण D दोनों को समद्विभाजित करता है।
(iv) भाग (ii) में हम सिद्ध कर चुके हैं कि
∆ABP ≅ ∆ACP
अतः BP = PC …..(1) [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।]
तथा ∠APB = ∠APC …..(vi) [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।]
अब ∠APB + ∠APC = 180°
(रैखिक युग्म अभिगृहीत से)
∠APB + ∠APB = 180°
[समीकरण (vi) के अनुसार
या 2∠APB = 180°
या ∠APB = 90°
अर्थात् AP ⊥ BC
समीकरण (v) से BP = PC तथा समीकरण (vii) के अनुसार यह सिद्ध किया है कि AP ⊥ BC । दोनों समीकरणों को सम्मिलित करने पर यह कहा जा सकता है कि AP रेखाखण्ड BC का लम्ब समद्विभाजक है।
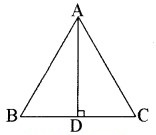
प्रश्न 2.
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि
(i) AD रेखाखण्ड BC को समद्विभाजित करता है।
(ii) AD कोण A को समद्विभाजित करता है।
हल:
प्रश्नानुसार दिए गए त्रिभुज के अनुसार ∆ABD और ∆ACD में
AB = AC (दिया है)
∠ADB = ∠ADC (प्रत्येक 90°) [क्योंकि AD ⊥ BC (दिया है)]
तथा AD = AD (उभयनिष्ठ भुजा)
अतः ∆ABD ≅ ∆ACD [सर्वांगसमता के नियम RHS से]
अतः BD = DC [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं]
(i) अर्थात् AD, BC को समद्विभाजित करती है। साथ ही ∠BAD = ∠CAD [क्योंकि सर्वांगसम त्रिभुजों के ये संगत भाग हैं।]
(ii) अर्थात् AD, ∠A को समद्विभाजित करती है।
प्रश्न 3.
एक त्रिभुज ABC की दो भुजाएँ AB और BC तथा माध्यिका AM क्रमशः एक-दूसरे त्रिभुज की भुजाओं PO और OR तथा माध्यिका PN के बराबर हैं ( देखिए आकृति)। दर्शाइए कि
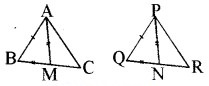
(i) ∆ABM ≅ ∆PQN
(ii) ∆ABC ≅ ∆PQR
हल:
प्रश्नानुसार AM, ∆ABC की माध्यिका हैं।

अतः BM = ON …..(iii) [समीकरण (i) व (ii) के अनुसार]
(i) अब ∆ABM और ∆PON में
AB = PQ (दिया है)
AM = PN (दिया है)
BM = QN [समीकरण (iii) के अनुसार]
अतः ∆ABM ≅ ∆PON
[सर्वांगसमता के SSS नियम के अनुसार]
अतः ∠B = ∠Q …..(iv) (क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं।)
(ii) अब ∆ABC और ∆PQR में AB = PQ (दिया है)
∠B = ∠Q [समीकरण (iv) के अनुसार]
तथा BC = QR (दिया है)
∴ ∆ABC ≅ ∆PQR
[सर्वांगसमता के SAS नियम के अनुसार]
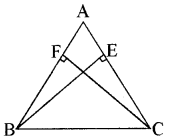
प्रश्न 4.
BE और CF एक त्रिभुज ABC के दो बराबर शीर्षलम्ब हैं। RHS सर्वांगसमता नियम का प्रयोग करके सिद्ध कीजिए कि ∆ABC एक समद्विबाहु त्रिभुज है।
हल:
प्रश्नानुसार त्रिभुज की रचना कर अब ∆BEC और ∆CFB में
∠BEC = ∠CFB [प्रत्येक 90°] [क्योंकि BE ⊥ AC और CF ⊥ AB]
BC = BC (उभयनिष्ठ भुजा)
तथा BE = CF (दिया है)
अतः ∆BEC ≅ ∆CFB
[सर्वांगसमता के नियम RHS के अनुसार] ।
अतः EC = FB [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं]
अब पुन: ∆AEB तथा ∆AFC में
∠AEB = ∠AFC [प्रत्येक 90° (दिया है)]
∠A = ∠A (उभयनिष्ठ कोण)
तथा EB = FC (दिया है)
अतः ∆AEB = ∆AFC (सर्वांगसमता के नियम AAS के अनुसार)
अतः AE = AF …..(ii)
[क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं] अब समीकरण (i) व (ii) को जोड़ने पर
EC + AE = FB + AF
या AC = AB
अब ∆ABC में हमें प्राप्त है AB = AC
अर्थात् ∆ABC एक समद्विबाहु त्रिभुज है। (इति सिद्धम्)
प्रश्न 5.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
हल:
दिया है–चित्रानुसार एक समद्विबाहु त्रिभुज ABC है जिसमें AB = AC

सिद्ध करना है – ∠B = ∠C रचना-भुजा BC पर लम्ब AP खींचा।
उपपत्ति – ∆ABP तथा ∆ACP से
∠APB = ∠APC [प्रत्येक कोण 90°]
(रचना से) AB = AC
(दिया है) AP = AP (उभयनिष्ठ भुजाएँ)
अत: ∆ABP = ∆ACP
(सर्वांगसमता के नियम RHS के अनुसार)
अतः B = ∠C [क्योंकि ये सर्वांगसम त्रिभुजों के संगत भाग हैं]