Chapter 10 Mensuration Ex 10.2
Question 1.
Find the areas of the following figures by counting square:

Solution:
(a) Number of full squares = 9
Area of 1 square = 1 sq unit
∴ Area of 9 squares = 9 x 1 sq unit
= 9 sq units.
So, the area of the portion covered by 9 squares = 9 sq units
(b) Number of full squares = 5
∴ Area of the figure = 5 x 1 sq unit = 5 sq units
(c) Number of full squares = 2
Number of half squares = 4
∴ Area of the covered figure = 2 x 1 + 4 x = 2 + 2
= 4 sq units
(d) Number of full squares = 8
∴ Area of the covered portion of the figure = 8 x 1 sq unit
= 8 sq units.
(e) Number of full squares = 10
Area covered by the figure = 10 x 1 sq unit = 10 sq units.
(f) Number of full squares = 2
Number of half squares = 4
∴ Area of the covered figure = (2 x 1 + 4 x )
= (2 + 2) sq units = 4 sq units.
(g) Number of full squares = 4
Number of half squares = 4
∴ Area of the covered figure = (4 x 1 + 4 x )
= (4 + 2) sq units = 6 sq units.
(h) Number of full squares = 5
∴ Area of the covered figure = 5 x 1 sq unit = 5 sq units.
(i) Number of full squares = 9
∴ Area of the covered figure = 9 x 1 sq units
= 9 sq units.
(j) Number of full squares = 2
Number of half squares = 4
∴ Area of the covered figure =(2 x 1 + 4 x ) sq units
= (2 + 2) sq units = 4 sq units.
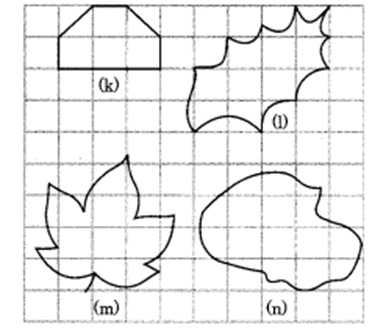
(k) Number of full squares = 4
Number of half squares = 2
∴ Area of the covered figure = (4 x 1 + 2 x )sq units
= (4 + 4)sq units
= 5sq units
(l) Number of full squares = 4
Number of squares more than half = 3
Number of half squares = 2
∴ Area of the covered figure = (4 x 1 + 3 x 1 + 2 x sq units
= (4 + 3 + 1) sq units = 8 sq units.
(m) Number of full squares = 6
Number of more than half squares = 8
Area of the covered figure = (6 x 1 + 8 x 1) sq units
= (6 + 8) sq units
= 14 sq units.
(n) Number of full squares = 9
Number of more than half squares = 9
∴ Area of the covered figure
= (9 x 1 + 9 x 1) sq units
= (9 + 9) sq units = 18 sq units.



