Chapter 1 पूर्णांक Ex 1.2
प्रश्न 1.
ऐसा पूर्णांक युग्म लिखिए जिसका
(a) योग -7 है
(b) अन्तर – 10 है
(c) योग 0 है।
हल:
(a) हम लेते हैं योग (-3) + (- 4) = – 7
∴ अभीष्ट पूर्णांक युग्म = -3 और -4
(b) हम लेते हैं अन्तर -15 – (-5) = – 10
∴अभीष्ट पूर्णांक युग्म = – 15 और -5
(c) हम लेते हैं योग – 25 + 25 = 0
∴ अभीष्ट पूर्णांक युग्म = – 25 और 25
प्रश्न 2.
(a) एक ऐसा ऋणात्मक पूर्णांक युग्म लिखिए जिसका अन्तर 8 है।
(b) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका योग-5 है।
(c) एक ऋणात्मक पूर्णांक और एक धनात्मक पूर्णांक लिखिए जिनका अन्तर – 3 है।
हल:
(a) चूँकि -2 – (-10) = – 2 + 10 = 8
अतः -2 और – 10 एक ऐसा ऋणात्मक पूर्णांक युग्म है जिनका अन्तर 8 है।
(b) चूँकि – 6 + 1 = -5
अतः -6 और 1 पूर्णांक युग्म है जिनका योग – 5 है और इनमें से एक पूर्णांक ऋणात्मक और एक धनात्मक है।
(c) चूँकि (-1) – (2) = – 1 – 2 = -3
अतः -1 और 2 पूर्णांक युग्म ऐसा है जिनका अन्तर – 3 है और इनमें से एक पूर्णांक ऋणात्मक और एक धनात्मक है।
प्रश्न 3.
किसी प्रश्नोत्तरी के तीन उत्तरोतर चक्करों (rounds) में टीम A द्वारा प्राप्त किए गए अंक -40, 10, 0 थे और टीम B द्वारा प्राप्त किए गए अंक 10, 0, – 40 थे। किस टीम ने अधिक अंक प्राप्त किए ? क्या हम कह सकते हैं कि पूर्णांकों को किसी भी क्रम में जोड़ा जा सकता है ?
हल:
टीम A के द्वारा प्राप्त किए गए अंकों का योग = (-40) + 10 + 0 = – 40 + 10 = – 30
टीम B के द्वारा प्राप्त किए गए अंकों का योग
= 10 + 0+ (-40) = 10 – 40 = -30
अतएव दोनों टीमों ने बराबर अंक प्राप्त किए हैं अर्थात् – 30
हाँ, हम कह सकते हैं कि पूर्णांकों को किसी भी क्रम में जोड़ा जा सकता है।
प्रश्न 4.
निम्नलिखित कथनों को सत्य बनाने के लिए रिक्त स्थानों की पूर्ति कीजिए
(i) (-5) + (-8) = (-8) + (….)
(ii) -53 + …. = – 53
(iii) 17+ …. = 0
(iv) [13 + (-12)] + (….)= 13 + [(-12) + (-7)]
(v) (-4)+ [15 + (-3)] = [-4+ 15] + ….
हल:
(i) चूँकि पूर्णांकों को किसी भी क्रम में जोड़ा जा सकता है,
∴ (-5) + (-8) = (-8) + (-5)
(ii) किसी पूर्णांक में शून्य जोड़ने पर वही संख्या प्राप्त होती है,
∴ -53 + 0 = -53
(iii) चूँकि किसी पूर्णांक और उसके योज्य प्रतिलोम का योग शून्य होता है,
∴ 17 + (-17) = 0
(iv) चूँकि पूर्णांकों के लिए योग सहचारी होता है, अर्थात् a+ (b + c) = (a + b) + c .
∴ [13 + (- 12)] + (-7) = 13 + [(- 12) + (-7)]
(v) ∴ (-4) + [15 + (-3)] = [(-4) + 15] + (-3)
प्रयास कीजिए
प्रश्न 1.
संख्या रेखा का उपयोग करते हुए ज्ञात कीजिए-
(i) 4 x (-8)
(ii) 8 x (-2)
(iii)3 x (-7)
(iv) 10 x (-1).
हल:
(i) 4 x (-8); इसे हम संख्या रेखा पर निम्नलिखित रूप में निरूपित कर सकते हैं,

अतः संख्या रेखा से, हम प्राप्त करते हैं :
(-8) + (-8) + (-8) + (-8) = -32
4 x (-8) = – 32
(ii) 8 x (-2); इसे हम संख्या रेखा पर निम्नलिखित रूप में निरूपित कर सकते हैं,

अब संख्या रेखा से, हम प्राप्त करते हैं
(-2) + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) + (-2) = – 16
∴ 8 x (-2) = -16
(iii) 3 x (-7); इसे हम संख्या रेखा पर निम्नलिखित रूप में निरूपित कर सकते हैं,
![]()
अब संख्या रेखा से, हम प्राप्त करते हैं :
(-7) + (-7) + (-7) = – 21
∴ 3 x (-7) = -21
(iv) 10 x (- 1); इसे संख्या रेखा पर हम निम्नलिखित रूप में निरूपित कर सकते हैं,
![]()
अब संख्या रेखा से, हम प्राप्त करते हैं :
(-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) + (-1) = – 10
∴ 10x (-1) = -10
पाठ्य-पुस्तक पृष्ठ संख्या # 11
निम्नलिखित को ज्ञात कीजिएहल :
(i) 4 x (-8)= – (4 x 8) = -32
(ii) 3 x (-7) = – (3 x 7) = – 21
(iii) 6 x (-5) = – (6 x 5) = -30
(iv) 2 – (-9) = – (2 x 9) = -18
प्रयास कीजिए
ज्ञात कीजिए-
(i) 6 x (-19)
(ii) 12 x (-32)
(iii) 7 x (-22)
हल:
(i) 6 x (-19) = – (6 x 19) = -114
(ii) 12 x (-32)= – (12 x 32) = – 384
(iii) 7x (-22) = – (7 x 22) = -154
पाठ्य-पुस्तक पृष्ठ संख्या # 12
प्रयास कीजिए
प्रश्न 1.
ज्ञात कीजिए-
(a) 15 x (-16)
(b) 21 x (-32)
(c) (-42) x 12
(d) (-55) x 15
हल:
एक धन पूर्णांक और एक ऋण पूर्णांक का गुणा करने के लिए पहले पूर्णांकों का गुणा करते हैं और तत्पश्चात् गुणनफल से पहले (-) का चिह्न लगा देते हैं।
(a) 15 x (-16) = -(15 x 16) = -240
(b) 21 x (-32) = – (21 x 32) =-672
(c) (-42) x 12 = – (42 x 12) = – 504
(d) (-55) x 15 = – (55 x 15) = – 825
प्रश्न 2.
जाँच कीजिए कि क्या
(a) 25 x (-21)=(-25) x 21 है।
(b) (-23) x 20 = 23 x (-20) है।
इस प्रकार के पाँच और उदाहरण लिखिए।
हल:
(a) L.H.S. = 25 x (-21) = – (25 x 21) = -525
R.H.S. = (-25) x 21 = – (25 x 21) = -525
∵ L.H.S. = R.H.S.
∴ 25 x (-21) = (-25) x 21.
(b) L.H.S. = (-23) x 20 = – (23 x 20) = – 460
R.H.S. = 23 x (-20) = – (23 x 20) = – 460
∵ L.H.S. = R.H.S.
∴ (-23) x 20 = 23 x (-20)
अन्य उदाहरण-
(i) (-13) x 20 = 13 – (-20)
(ii) 25 x (-17) = (-25) x 17
(iii) 50x (-40) = (-50) x 40
(iv) 75 x (- 12) = (-75) x 12
(v) 91 x (-25) = (-91) x 25
पाठ्य-पुस्तक पृष्ठ संख्या # 13
प्रेक्षणों के आधार पर निम्नलिखित को पूरा कीजिए-
(i) -3 x – 3 = …,
(ii) -3x – 4 = …..
हल:
(i) – 3 x 4 = – 12
-3 x 3 = -9 = – 12 – (-3) = – 12 + 3
– 3 x 2 = – 6 = -9 – (-3) = -9 + 3
– 3 x 1 = -3 = – 6 -(-3) = – 6 + 3
-3 x 0 = 0 = -3 -(-3)= – 3 +3
-3x – 1 = 0 – (-3) = 0 + 3 = 3
-3x -2 = 3 – (-3) = 3 + 3 = 6
– 3 x -3 = 6 – (-3) = 6 + 3 = 9
अतएव, -3 x -3 = 9
(ii) -3 x – 4.
– 3 x 4 = – 12
– 3 x 3 = – 9 = – 12 -(-3) = – 12 + 3
– 3 x 2 = – 6 = – 9 – (-3)= – 9 +3
– 3 x 1 = -3 = -6 – (-3)= – 6 + 3
– 3 x 0 = 0 = -3 – (-3)= -3 + 3
– 3 x – 1 = 0 – (-3) = 0 + 3 = 3
– 3 x – 2 = 3-(-3)= 3 + 3 = 6
– 3 x -3 = 6-(-3)= 6 + 3 = 9
– 3 x – 4 = 9 – (-3) = 9 + 3 = 12
अतएव, – 3 x -4 = 12
इन गुणनफलों को देखिए और रिक्त स्थानों की पूर्ति कीजिए
– 4 x 4 = – 16
– 4 x 3 = – 12 = – 16 + 4
– 4 x 2 = -8 = – 12 +4
– 4 x 1 = -4 = -8 + 4
– 4 x 0 = 0 = -4 + 4
– 4 x (-1) = 4 = 0 + 4
– 4 x (-2) = 8 = 4 + 4
– 4 x (-3) = 12 = 8 + 4
अतएव,
(-4) x (-2) = 4 x 2 = 8
(-4) x (-3) = 4 x 3 = 12
प्रयास कीजिए
(i) (-5) x 4, से शुरू करते हुए (-5) x (-6) ज्ञात कीजिए।
(ii) (-6) x 3, से शुरू करते हुए (-6) x (-7) ज्ञात कीजिए।
हल:
(i) (-5) x 4 = -(5 x 4) = -20
(-5) x 3 = -(5 x 3) = -15 = -20 + 5
(-5) x 2 = -(5 x 2)= -10 = – 15 + 5
(-5) x 1 = -(5 x 1) = -5 = -10 + 5
(-5) x 0 = – (5 x 0)= 0 = -5 + 5
इस पैटर्न से, हम प्राप्त करते हैं :
(-5) x (-1) = 0 + 5 = 5
(-5) x (-2) = 5 + 5 = 10
(-5) x (-3) = 10 + 5 = 15
(-5) x (-4) = 15 + 5 = 20
(-5) x (-5) = 20+ 5 = 25
(-5) x (-6) = 25+ 5 = 30
अतएव, (-5) x (-6) = 30
(ii) (-6) x 3 – (6 x 3) = -18
(-6) x 2 = -(6 x 2)= – 12 = – 18 + 6
(-6) x 1 = -(6 x 1) -6 = -12 + 6
(-6) x 0 = -(6 x 0) = 0 = – 6 + 6
इस पैटर्न से, हम प्राप्त करते हैं :
(-6) x (-1) = 0 + 6 = 6
(-6) x (-2) = 6 + 6 = 12
(-6) x (-3) = 12 + 6 = 18
(-6) x (-4) = 18 + 6 = 24
(-6) x (-5) = 24 + 6 = 30
(-6) x (-6) = 30+6 = 36
(-6) x (-7) = 36+ 6 = 42
प्रयास कीजिए
प्रश्न 1.
ज्ञात कीजिए-
(-31) x (-100), (-25) x (-72), (-83) x (-28)
हल:
(-31) (-100) = + (31 x 100)= 3100
(-25) x (-72) = + (25 x 72)= 1800
(-83) x (-28) = + (83 x 28) = 2324
पाठ्य-पुस्तक पृष्ठ संख्या # 15
तीन अथवा अधिक ऋणात्मक पूर्णांकों का गुणनफल
प्रश्न (d) में पाँच ऋणात्मक पूर्णांकों का गुणनफल क्या है ? 6 ऋणात्मक पूर्णांकों का गुणनफल क्या होगा ?
हल:
(d) में पाँच ऋणात्मक पूर्णांकों का गुणनफल ऋणात्मक होगा।
6 ऋणात्मक पूर्णांकों का गुणनफल धनात्मक होगा।
नोट: यदि गुणा किये जाने वाले ऋणात्मक पूर्णांकों की संख्या सम हो, तो गुणनफल धनात्मक होगा और यदि गुणा किए जाने वाले ऋणात्मक पूर्णांकों की संख्या विषम है, तो गुणनफल ऋणात्मक पूर्णांक होगा।
प्रत्येक प्रकार के पाँच और उदाहरण देकर इस कथन की पुष्टि कीजिए।
उदाहरण 1.
जबकि ऋणात्मक पूर्णांकों की संख्या सम है-
(i) (-3) x (-4) = 12
(ii) (-1) (-5) x (-3) (-2) = {(-1)x (-5)} x {(-3) x (-2)} = 5 x 6 = 30
(iii) (-2) x (-3) x (-4) x (-5) x (-6) x (-7) = {(-2)x (-3)}x {(-4) x (-5)} x {(-6) x (-7)}
= 6 x 20 x 42 = 5040
(iv) (-3) x 5 x (-6) = (-3) x (-6) x 5 = 18 x 5 = 90
(v) (-2) – (-4) x (-5) x (-5) x 7
= {(-2)x (-4)} x {(-5)x (-5)} x 7 = 8 x 25 x 7 = 1400
उदाहरण 2.
जबकि ऋणात्मक पूर्णांकों की संख्या विषम है-
(i) (-2)x (-3) x (-5) = [(-2) x (-3)] x (-5) = 6 x (-5) = -30
(ii)(-4) x (-5) x (-3) x (-4) x (-6)
=[(-4)x (-5)] x [(-3)x (-4)] x (-6)
= 20 x 12 x (-6) = -1440
(iii)(-6) (-7) x 8 x (-5)
= [(-6) x (-7)] x 8x (-5) = 42 x 8 x (-5) = -1680
(iv) 3x (-10) x (-5)x (-8)
= 3 x (-10)x [(-5)x (-8)]
= -30 x 40 = -1200
(v) (-2) (-3) x (-4)x – 5x (-8)
= [(-2) (-3)] x [(-4) x (-8)] x -5
= 6 x 32 x (-5) = – 960
सोचिए, चर्चा कीजिए और लिखिए
प्रश्न (i).
गुणनफल (-9) x (-5) x (-6) (-3) धनात्मक है, जबकि गुणनफल (-9) x (-5) x 6 x (-3) ऋणात्मक है। क्यों ?
(ii) गुणनफल का चिह्न क्या होगा, यदि हम निम्नलिखित को एक साथ गुणा करते हैं ?
(a) आठ ऋणात्मक पूर्णांक एवं तीन धनात्मक पूर्णांक
(b) पाँच ऋणात्मक पूर्णांक और चार धनात्मक पूर्णांक
(c) (-1) को बारह बार
(d) (-1) को 2 m बार, जहाँ m एक प्राकृतिक संख्या है।
हल:
(i) गुणनफल (-9) x (-5) – (-6) x (-3) धनात्मक है क्योंकि यहाँ सम ऋणात्मक पूर्णांकों का गुणा किया गया है।
गुणनफल (-9) x (-5) x 6 x (-3) ऋणात्मक है क्योंकि यहाँ विषम ऋणात्मक पूर्णांकों का गुणा किया गया है।
(ii) (a) धनात्मक, ∵ आठ ऋणात्मक पूर्णांकों का गुणनफल धनात्मक है।
(b) ऋणात्मक, ∵ पाँच ऋणात्मक पूर्णांकों का गुणनफल ऋणात्मक है।
(c) धनात्मक,∵ 12 सम संख्या है अतः (-1) का बारह बार गुणनफल धनात्मक होगा।
(d) धनात्मक,∵ 2m राशि सम संख्या है। अतः (-1) 2m बार गुणा करने पर धन संख्या प्राप्त होगी। उत्तर
पाठ्य-पुस्तक पृष्ठ संख्या # 16
गुणन के अन्तर्गत संवृत
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए।
हल:
कथन निष्कर्ष
(-20) x (-5) = 100 गुणनफल एक पूर्णांक है
(-15) x 17 = – 255 गुणनफल एक पूर्णांक है
(-30) x 12 = – 360 गुणनफल एक पूर्णांक है
(-15) x (-23)= 345 गुणनफल एक पूर्णांक है
(-14) x (-13) = 182 गुणनफल एक पूर्णांक है
12 x (-30) = – 360 गुणनफल एक पूर्णांक है
पाँच और पूर्णांक युग्मों के गुणनफल ज्ञात कीजिए और उपर्युक्त कथन (सभी पूर्णांकों a तथा b के लिए a x b एक पूर्णांक होता है) को सत्यापित कीजिए।
उदाहरण:

गुणन के क्रम-विनिमेयता
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए :
कथन 2
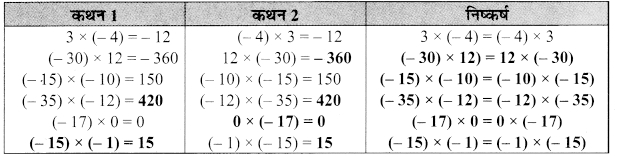
हम यहाँ देखते हैं कि दो पूर्णांकों का गुणनफल सदैव एक पूर्णांक होता है।
पाठ्य-पुस्तक पृष्ठ संख्या # 17
इस प्रकार के पाँच और उदाहरण लिखिए एवं सत्यापन कीजिए।
उदाहरण:
शून्य से गुणन -5 x 0 = 0
0 x (-6) = 0
गुणात्मक तत्समक
जाँच कीजिए कि 1 पूर्णांकों के लिए भी गुणनात्मक तत्समक है। 1 के साथ पूर्णांकों के निम्नलिखित गुणनफलों को देखिए :
(-3) x 1 = -3 1 x 5 = 5
(-4) x 1 = -4 1 x 8 = 8
1 x (-5) = -5 3 x 1 = 3
1 x (-6) = -6 7 x 1 = 7
यदि किसी भी पूर्णांक को – 1 से गुणा किया जाए, तो क्या होता है? निम्नलिखित को पूरा कीजिए :
(-3) x (-1) = 3
3 x (-1) = -3
(-6) x (-1) = 6
(-1) x 13 = – 13
(-1) x 25 = -25
18 x (-1) = -18
पाठ्य-पुस्तक पृष्ठ संख्या # 18
गुणन साहचर्य गुण
निम्नलिखित पर विचार कीजिए और गुणनफलों को पूरा कीजिए :
हल:
[7x (-6)] x 4 = -42 x 4 = -168
7 x [(-6) x 4] = 7 x (-24) = -168
क्या [7 x (-6)] x 4 = 7x [(-6) x 4] है?
हल:
L.H.S. = [7 x (-6)] x 4 = (-42) x 4=- 168
R.H.S. = 7 x [(-6) x 4] = 7 x (-24) = – 168
∴ L.H.S. = R.H.S.
अतः [7 x (-6)] x 4 = 7x [(-6) x 4]
अतएव किन्हीं तीन पूर्णांक a, b, c के लिए
[a x b] x c = a x [b x c]
a, b और c में से प्रत्येक के लिए पाँच मान लीजिए और इस गुण का सत्यापन कीजिए।
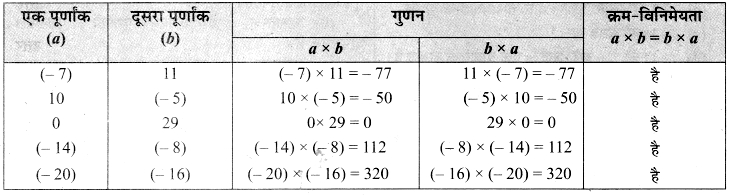
(a x b) x c = a x (bx c) का सत्यापन

अतएव तीन पूर्णांकों का गुणन सहचारी है। अर्थात् (a x b) x c = a x (b x c)
वितरण गुण
a,b और c में से प्रत्येक के लिए कम-से-कम पाँच मान लीजिए और वितरण गुण [a x (b + c)] = [a x b + a x c] को सत्यापित कीजिए।
उदाहरण:

अतः a x (b + c) = ax b + ax c के मान समान हैं।
प्रयास कीजिए
प्रश्न (i) क्या 10 x [6 + (-2)] = 10 x 6 + 10 x (-2) है ?
(ii) क्या (-15) x [(-7) + (-1) = (-15) x (-7) + (-15) x (-1) है ?
हल:
(i) हाँ, [∵ a x (b + c) = a x b + a x c]
(ii) हाँ, [∵ a x (b + c) = a x b + a x c]
किन्हीं तीन पूर्णांकों a, b और c के लिए
a x (b – c) = a x b – a x c
a, b और c के लिए कम-से-कम पाँच मान लीजिए और इस गुण को सत्यापित कीजिए।
उदाहरण:
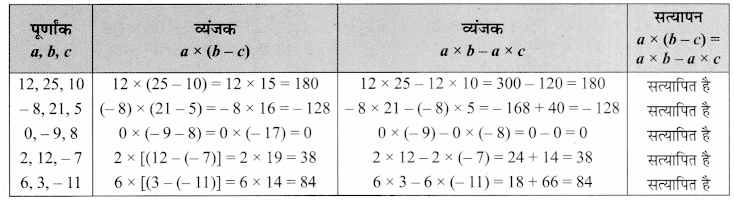
अतः a x (b – c) = a x b – a x c के मान समान हैं।
प्रयास कीजिए
प्रश्न
(i) क्या 10 x [6 – (-2)] = 10 x 6 – 10 x (-2) हैं?
(ii) क्या (-15) x [(-7) – (-1)] = (-15) x (-7) -(-15) x (-1) है ?
हल:
(i) हाँ, [∵ a x (b – c) = a x b – a x c]
(ii) हाँ, [∵ a x (b – c) = a x b – a x c]
पाठ्य-पुस्तक पृष्ठ संख्या # 20
प्रयास कीजिए
प्रश्न 1.
वितरण गुण का उपयोग करते हुए (-49) x 18; (-25) x (-31) ; 70 x (-19) + (-1) x 70 के मान ज्ञात कीजिए।
हल:
(i) (-49) x 18 :
∵ 18 = 10 + 8
∴ (-49) x 18 = (-49) x (10 + 8)
= (-49) x 10 + (-49) x 8
= -490 + (-49) (10 – 2) (∵ 8 = 10 – 2)
= – 490 + (-49) x 10 – (-49) x 2
= – 490 + (-490) + 98
= -980 + 98 = -882
(ii) (-25) x (-31):
∴ -31 = (-30) + (-1)
∴ (-25) x (-31)
= (-25) x [(-30) + (-1)]
= (-25) – (-30) + (-25) x (-1)
= 25 x 30 + 25 x 1
= 750 + 25 = 775
(iii) 70 x (-19) + (-1) x 70 :
= 70 x [(- 19) + (-1)]
[∵ a x b + a x c = a x (b + c) से]
= 70 x (-20)
= – (70 x 20) = -1400