Chapter 6 त्रिभुज और उसके गुण Ex 6.5
प्रश्न 1.
PQR एक त्रिभुज है जिसका P एक समकोण है। यदि PQ = 10 cm तथा PR = 24 cm तब QR ज्ञात कीजिए।
हल:
समकोण त्रिभुज PQR में पाइथागोरस प्रमेय का प्रयोग करने पर,
QR2 = PQ2 + PR2
OR2 = (10)2 + (24)2
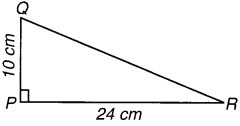
या QR2 = 100 + 576 = 676
या QR2 = (26)2
∴ QR = 26 cm
प्रश्न 2.
ABC एक त्रिभुज है जिसका ∠C एक समकोण है। यदि AB = 25 cm तथा AC = 7 cm तब BC ज्ञात कीजिए।
हल:
समकोण त्रिभुज ABC में पाइथागोरस प्रमेय का प्रयोग करने पर,
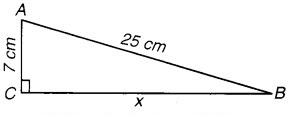
AC2 + BC2 = AB2
(7)2 + x2 = (25)2
या 49 + x2 = 625
या x2 = 625 – 49 = 576
या x2 = 242 ⇒ x = 24
∴ BC = 24 cm
प्रश्न 3.
दीवार के सहारे उसके पैर कुछ दूरी पर टिका कर 15 m लम्बी एक सीढ़ी भूमि से 12 m ऊँचाई पर स्थित खिड़की तक पहुँच जाती है। दीवार से सीढ़ी के पैर की दूरी ज्ञात कीजिए।
हल:
माना कि सीढ़ी के पैर दीवार से am की दूरी पर हैं।
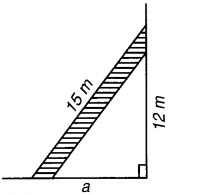
∴ पाइथागोरस प्रमेय से,
a2 + 122 = 152
या a2 + 144 = 225
या a2 = 225 – 144 = 81
शस a2 = (9)2 ⇒ a = 9m
अत: सीढ़ी के पैर की दीवार से अभीष्ट दूरी = 9 m
प्रश्न 4.
निम्नलिखित में भुजाओं के कौन-से समूह एक समकोण त्रिभुज बना सकते हैं?
(i) 2.5 cm, 6-5 cm,6cm
(ii) 2 cm, 2 cm, 5 cm
(iii) 1.5 cm, 2 cm, 2.5 cm
हल:
(i) माना, त्रिभुज की भुजाएँ x = 2.5 cm, y = 6.5 cm, z = 6 cm हैं।
यहाँ, सबसे बड़ी भुजा की लम्बाई y = 6.5 cm
अब, x2 + z2 = (2.5)2 + (6)2 = 6.25 + 36
= 42.25
तथा, y2 = (6.5)2 = 42.25,
∵ x2 + z2 = y2
अतः दी गई भुजाएँ समकोण त्रिभुज बना सकती हैं और भुजा 6.5 cm के सामने का कोण समकोण होगा।
(ii) माना त्रिभुज की भुजाएँ x = 2 cm, y = 2 cm, z = 5 cm है।
यहाँ, सबसे बड़ी भुजा की लम्बाई z = 5 cm है।
अब, x2 + y2 = (2)2 + (2)2
= 4 + 4 = 8
तथा z2 = (5)2 = 25
अत: अत: दी गई भुजाएँ समकोण त्रिभुज नहीं बना सकती हैं।
(iii) माना, त्रिभुज की भुजाएँ x = 1.5 cm, y = 2 cm और z = 2.5 cm हैं।
यहाँ, सबसे बड़ी भुजा की लम्बाई z = 2.5 cm है।
अब, x2 + y2 = (1.5)2 + (2)2 = 2.25 + 4.00
= 6.25
तथा z2 = (2.5)2 = 6.25,
∵ x2 + y2 = z2
अतः दी गई भुजाएँ समकोण त्रिभुज बना सकती हैं और भुजा 2.5cm के सामने का कोण समकोण होगा।
प्रश्न 5.
एक पेड़ भूमि से 5m की ऊँचाई पर टूट गया है और उसका ऊपरी सिरा भूमि को उसके आधार से 12 m की दूरी पर छूता है। पेड़ की पूरी ऊँचाई ज्ञात कीजिए।
हल:
माना कि पेड़ BD बिन्दु C से टूटा है,
इस प्रकार, CD = CA
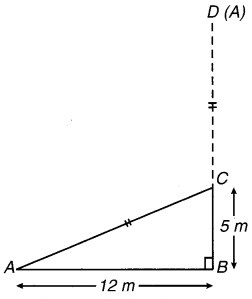
अब पाइथागोरस प्रमेय से, ∆ABC में,
AB2 + BC2 = AC2
122 + 52 = AC2
या 144 + 25 = AC2
या AC2 = 169 = 132
या AC = 13 m
अब, पेड़ की ऊँचाई = BD = BC + CD
= BC + AC (∵AC = CD)
= 5 m + 13 m = 18 m
अतः पेड़ की अभीष्ट लम्बाई = 18 m
प्रश्न 6.
त्रिभुज PQR में कोण Q = 25° तथा कोण R = 25° है। अग्रलिखित में कौन-सा कथन सत्य है ?
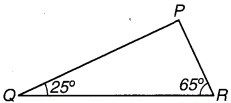
(i) PQ2 + QR = RP
(ii) PQ2 + RP2 = QR2
(iii) RP2 + QR2 = PQ2
हल:
∆PQR में,
∠P + ∠Q + ∠R = 180°
∠P + 25° + 65° = 180°
या ∠P + 90° = 180°
या ∠P = 180° – 90° = 90°
अत: ∆PQR समकोण त्रिभुज है, जिसका कोण P समकोण है।
अब, कर्ण = कोण P के सामने की भुजा = QR पाइथागोरस प्रमेय द्वारा
QR2 = PQ2 + PR2
अतः सम्बन्ध (ii) PQ2 + RP2 = QR2 सत्य है।
प्रश्न 7.
एक आयत की लम्बाई 40 cm है तथा उसका एक विकर्ण 41 cm है। इसका परिमाप ज्ञात कीजिए।
हल:
आयत की लम्बाई = 40 cm, विकर्ण = 41 cm
माना कि आयत की चौड़ाई = x cm
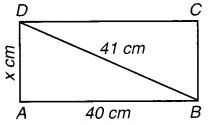
समकोण त्रिभुज BAD से,
AB2 + AD2 = BD2
402 + AD2 = 412
या AD2 = 412 – 402 = 1681 – 1600
= 81 = 92
∴ चौड़ाई x = 9 cm
अब परिमाप = 2 (लम्बाई + चौड़ाई)
= 2 (40 + 9) = 2 × 49 = 98 cm
अत: आयत का परिमाप = 98 cm
प्रश्न 8.
एक समचतुर्भुज के विकर्ण 16 cm तथा 30 cm हैं। इसका परिमाप ज्ञात कीजिए।
हल:
माना कि ABCD एक समचतुर्भुज है, जिसमें AC = 30 cm और BD = 16 cm.
हम जानते हैं कि समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर काटते हैं। (यहाँ ये O पर काटते हैं।)
∠AOB = 90°
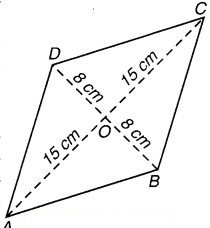
अब समकोण ∆AOB में,
AB2 = 40 + BO2
= 152 + 82
= 225 + 64 = 289
या AB2 = 172 ⇒ AB = 17
∴ समचतुर्भुज का परिमाप = 4 × AB = 4 × 17 cm
= 68 cm
पाठ्य-पुस्तक पृष्ठ संख्या # 143
सोचिए, चर्चा कीजिए एवं लिखिए
प्रश्न 1.
त्रिभुज PQR का कोण P एक समकोण है। इसकी सबसे लम्बी भुजा कौन-सी है?
हल:
∵ शीर्ष P पर कोण 90° बनता है।
∴ समकोण बनाने वाली भुजाएँ PQ और PR हैं।
∴ कर्ण = QR
अत: त्रिभुज की सबसे लम्बी भुजा QR है।
प्रश्न 2.
त्रिभुज ARC का कोण B एक समकोण है। इसकी सबसे लम्बी भुजा कौन-सी है ?
हल:
शीर्ष B पर कोण 90° बनता है।
∴ ∆ABC की समकोण बनाने वाली भुजाएँ AB और BC हैं।
∴ कर्ण = AC
अतः त्रिभुज की सबसे लम्बी भुजा AC है।
प्रश्न 3.
किसी समकोण त्रिभुज में सबसे लम्बी भुजा कौन-सी होती है ?
हल:
समकोण त्रिभुज में सबसे लम्बी भुजा कर्ण होती है।
प्रश्न 4.
किसी आयत में विकर्ण पर बने वर्ग का क्षेत्रफल उसकी लम्बाई तथा चौड़ाई पर बने वर्गों के क्षेत्रफल के योग के बराबर होता है। यह बौधायन का प्रमेय है। इसकी पाइथागोरस गुण से तुलना कीजिए।
हल:
पाइथागोरस प्रमेय के अनुसार, “समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।” बौधायन ने सुलभ सूत्र में कहा है कि “आयत के कर्ण द्वारा बनाया गया क्षेत्रफल उसकी दोनों भुजाओं के द्वारा बनाये गये क्षेत्रफल के बराबर होता है।”
अब, माना कि आयत की लम्बाई और चौड़ाई क्रमशः a और b है तथा इसका विकर्ण c है। इसलिए विकर्ण पर बने वर्ग का क्षेत्रफल = c × c = c2 तथा आयत की भुजाओं पर बने वर्गों के क्षेत्रफल a2 और b2 हैं।
∴ c2 = a2 + b2 (बौधायन सुलभ सूत्र)
अतः स्पष्ट है कि पूर्व में बौधायन कथन ही वर्तमान में पाइथागोरस प्रमेय है।