Chapter 14 सममिति Ex 14.1
प्रश्न 1.
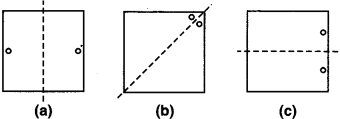
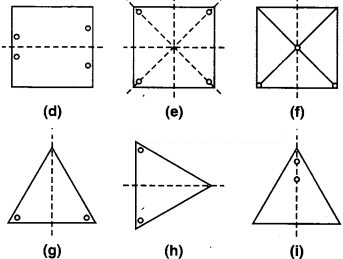
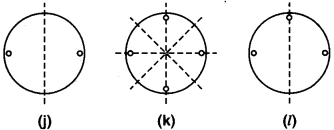
पाठ्य-पुस्तक में दी गई छेद की हुई आकृतियों की प्रतिलिपियाँ बनाकर (खींचकर) उनमें से प्रत्येक की सममित रेखाएँ ज्ञात कीजिए।
हल:
सममित रेखाएँ बिन्दुकित रेखाओं से निरूपित हैं।
प्रश्न 2.
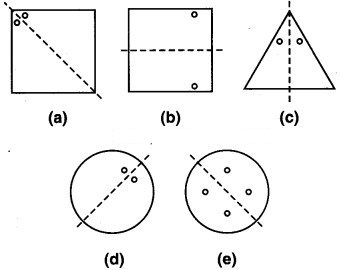
पाठ्य-पुस्तक में दी गई आकृतियों में सममित रेखा (रेखाएँ) दी हुई हैं। अन्य छेद ज्ञात कीजिए।
हल:
निम्नांकित आकृतियों में अन्य छेद दर्शाए गए हैं :
प्रश्न 3.
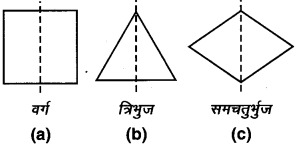
पाठ्य-पुस्तक में दी हुई आकृतियों में दर्पण रेखा (अर्थात् सममित रेखा) बिन्दुकित रेखा के रूप में दी गई है। बिन्दुकित (दर्पण) रेखा में प्रत्येक आकृति का परावर्तन करके, प्रत्येक आकृति को पूरा कीजिए। (आप बिन्दुकित रेखा के अनुदिश एक दर्पण रख सकते हैं और फिर प्रतिबिम्ब (image) के लिए दर्पण में देख सकते हैं)। क्या आपको पूरी की गई आकृति का नाम याद है ?
हल:
प्रत्येक आकृति की पूर्ण आकृति (परावर्तित आकृति) दर्शाई गई है:

प्रश्न 4.
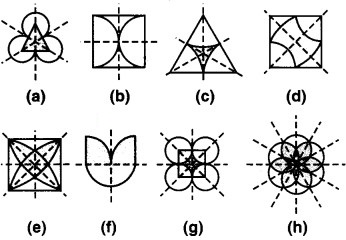
पाठ्य-पुस्तक में दी हुई आकृतियों में से प्रत्येक में विविध सममित रेखाओं (यदि हों तो) की पहचान कीजिए।
हल:
निम्नांकित आकृतियों में विविध सममित रेखाएँ दर्शाई गई हैं:
प्रश्न 5.
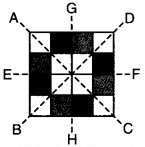
पाठ्य-पुस्तक में दी हुई आकृति की प्रतिलिपि बनाइए। किसी एक विकर्ण की सममित रेखा लीजिए तथा कुछ और वर्गों को इस तरह छायांकित कीजिए कि यह आकृति इस विकर्ण के अनुदिश सममित हो जाए। क्या ऐसा करने की एक से अधिक विधियाँ हैं ? क्या यह आकृति दोनों विकर्णों के अनुदिश सममित होगी?
हल:
- आकृति विकर्ण AC के अनुदिश सममित है।
- चूँकि आकृति EF और GH के अनुदिश सममित हैं। अत: यह एक से अधिक रेखा के अनुदिश सममित है।
-
यह आकृति विकर्ण BD के भी अनुदिश सममित है।
प्रश्न 6.
पाठ्य-पुस्तक में दिये हुए आरेखों की प्रतिलिपियाँ बनाइए तथा प्रत्येक आकार को इस तरह पूरा कीजिए ताकि वह आकार दर्पण रेखा (या रेखाओं) के अनुदिश सममित हो।
हल:
आरेखों की दर्पण रेखा के अनुदिश सममिति निम्न प्रकार है:

प्रश्न 7.
निम्नलिखित आकृतियों के लिए सममित रेखाओं की संख्याएँ बताइए:
(a) एक समबाहु त्रिभुज
(b) एक समद्विबाहु त्रिभुज
(c) एक विषमबाहु त्रिभुज
(d) एक वर्ग
(e) एक आयत
(f) एक समचतुर्भुज
(g) एक समान्तर चतुर्भुज
(h) एक चतुर्भुज
(i) एक समषट्भुज
(j) एक वृत्त
हल:
(a) एक समबाहु त्रिभुज – 3 सममित रेखाएँ
(b) एक समद्विबाहु त्रिभुज – 1 सममित रेखा
(c) एक विषमबाहु त्रिभुज – 0 (शून्य) समपित रेखा
(d) एक वर्ग – 4 सममित रेखाएँ
(e) एक आयत – 2 सममित रेखाएँ
(f) एक समचतुर्भुज – 2 सममित रेखाएँ
(g) एक समान्तर चतुर्भुज – 0 (शून्य) सममित रेखा
(h) एक चतुर्भुज – 0 (शून्य) सममित रेखा
(i) एक समषट्भुज – 6 सममित रेखाएँ
(j) एक वृत्त – असीमित सममित रेखाएँ
प्रश्न 8.
अंग्रेजी वर्णमाला के किन अक्षरों में निम्नलिखित के अनुदिश परावर्तन सममिति (दर्पण परावर्तन से सम्बन्धित सममिति) है :
(a) एक ऊर्ध्वाधर दर्पण
(b) एक क्षैतिज दर्पण
(c) ऊर्ध्वाधर और क्षैतिज दर्पण दोनों।
हल:
(a) एक ऊर्ध्वाधर दर्पण में निम्न अंग्रेजी वर्णमाला के अक्षरों में परावर्तन सममिति है :
A, H, I, M, O, T, U, V, W,X और Y.
(b) क्षैतिज दर्पण के अनुदिश अंग्रेजी अक्षर, जिनमें परावर्तन सममिति है:
B,C, D, E, H, I,O और X.
(c) अंग्रेजी अक्षर, जिनमें ऊर्ध्वाधर और क्षैतिज दर्पणों के अनुदिश परावर्तन्द सममिति है :
H, I, O और X.
प्रश्न 9.
ऐसे आकारों के तीन उदाहरण दीजिए, जिनमें कोई सममित रेखा न हो।
उत्तर:
ऐसे आकार जिनमें सममित रेखा नहीं है :
- एक विषमबाहु त्रिभुज
- एक अनियमित चतुर्भुज
- अक्षर F.
प्रश्न 10.
आप निम्नलिखित आकृतियों की सममित रेखा के लिए अन्य क्या नाम दे सकते हैं ?
(a) एक समद्विबाहु त्रिभुज
(b) एक वृत्त।
उत्तर:
(a) माध्यिका
(b) वृत्त का व्यास।
पाठ्य-पुस्तक पृष्ठ संख्या # 288 प्रयास कीजिए
प्रश्न 1.
(a) क्या अब आप एक समबाहु त्रिभुज के लिए, घूर्णन सममिति के क्रम को बता सकते हैं (संलग्न आकृति) ?
(b) जब उपरोक्त त्रिभुज को उसके केन्द्र के परितः (चारों ओर) 120° के कोण पर घुमाया जाता है, तो कितनी स्थितियों में त्रिभुज (स्थिति के अनुसार) पहले जैसा ही लगता है ?
हल:
(a) ∵ ऐसी तीन स्थितियाँ हैं जहाँ कि त्रिभुज एक जैसे दिखाई देंगे। अतः इसमें क्रम 3 की घूर्णन स्थितियाँ हैं। (120°,240°,360°)
(b) यहाँ केवल एक स्थिति होगी, जबकि त्रिभुज ठीक पहले जैसी स्थिति में दिखाई देगा, जबकि इसे केन्द्र के परितः 120° पर घुमाया जाएगा।
प्रश्न 2.
निम्नलिखित में से कौन-से आकारों (संलग्न आकृति) में अंकित बिन्दुओं के परितः (चारों ओर) घूर्णन सममिति है।
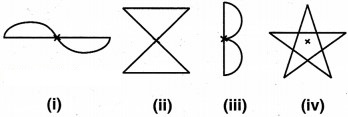
हल:
क्योंकि हम जानते हैं कि जब कोई आकृति एक कोण के द्वारा एक बिन्दु पर घूर्णन करती है और पहले जैसी दिखाई देती है, तो उसे घूर्णन सममिति कहते हैं। इस प्रकार, आकृति (i), (ii) व (iv) में घूर्णन सममिति है।
इन्हें कीजिए
दो एक जैसे (सर्वांगसम चतुर्भुज खींचिए, एक समान्तर चतुर्भुज ABCD एक कागज पर तथा दूसरा समान्तर चतुर्भुज A’B’C’D’ एक पारदर्शक शीट (Transparent sheet) पर। उनके विकर्णों के प्रतिच्छेद बिन्दुओं को क्रमशः 0 और 0′ से अंकित (या व्यक्त) कीजिए। समान्तर चतुर्भुजों को इस प्रकार रखिए कि A’ शीर्ष A पर रहे, B’ शीर्ष B पर रहे, इत्यादि।
इन आकारों में, अब बिन्दु O पर एक पिन लगाइए। अब पारदर्शक शीट को दक्षिणावर्त दिशा में घुमाइए।

प्रश्न (i) एक पूरे चक्कर में पारदर्शकशीट पर बना आकार कागज पर बने आकार से कितनी बार संपाती होता है।
(ii) इसमें घूर्णन सममिति का क्या क्रम है ?
हल:
(i) जब हम पारदर्शक शीट को दक्षिणावर्त दिशा में घुमाते हैं, तो दो स्थितियाँ प्राप्त होती हैं। पहली स्थिति में जब शीर्ष A’ शीर्ष A पर होता है और दूसरी स्थिति में शीर्ष A’ शीर्ष C पर होता है। इससे स्पष्ट होता है कि पूरा चक्कर घुमाने (360°) पर समान्तर चतुर्भुज की दो स्थितियाँ हैं, जहाँ यह एक जैसा दिखाई देगा।
(ii) इसमें क्रम 2 की घूर्णन सममिति होगी।
पाठ्य-पुस्तक पृष्ठ संख्या # 289
प्रयास कीजिए
प्रश्न 1.
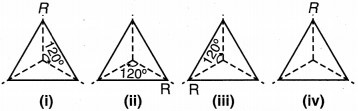
दी हुई आकृतियों के लिए x से अंकित बिन्दु के परितः घूर्णन सममिति का क्रम बताइए (संलग्न आकृति)।
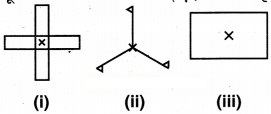
हल:
जब आकृति (i) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति चार स्थितियों (90°, 180°,270° और 360°) में मूल आकृति जैसी दिखती है। अतः आकृति (i) में क्रम 4 की घूर्णन सममिति होगी।
जब आकृति (ii) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति तीन स्थितियों (120°, 240° और 360°) में | मूल आकृति जैसी दिखती है। अतः आकृति (ii) में क्रम 3 की घूर्णन सममिति होगी।
जब आकृति (iii) को अंकित बिन्दु के परितः घुमाया जाता है, तो यह आकृति दो स्थितियों (180° और 360°) में मूल आकृति जैसी दिखती है। अतः आकृति (iii) में क्रम 2 की घूर्णन सममिति होगी।
पाठ्य-पुस्तक पृष्ठ संख्या # 290