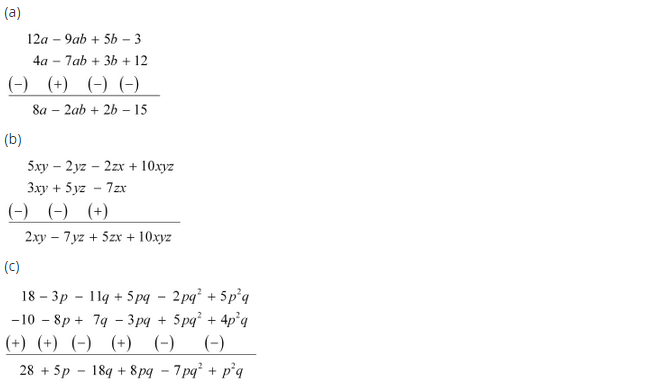Chapter 9 Algebraic Expressions and Identities Exercise 9.1
Question 1.
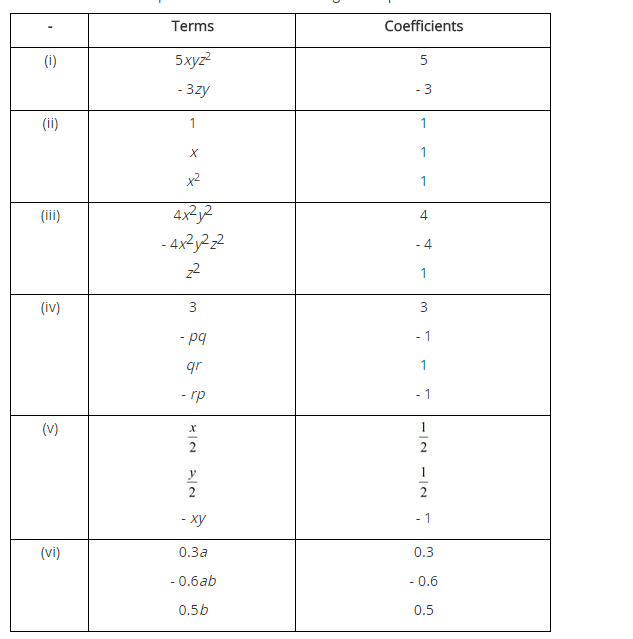
Identify the terms, their coefficients for each of the following expressions.
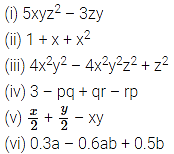
Solution:
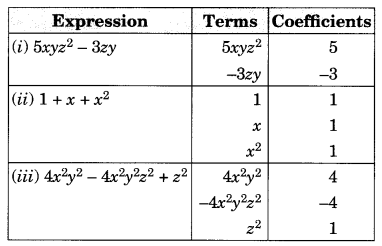
Question 2.
Classify the following polynomials as monomials, binomials, trinomials. Which polynomials do not fit in any of these three categories?
x + y, 1000, x + + + , 7 + y + 5x, 2y – 3, 2y – 3 + 4, 5x – 4y + 3xy, 4z – 15, ab + bc + cd + da, pqr, q + p, 2p + 2q
Solution:

Question 3.
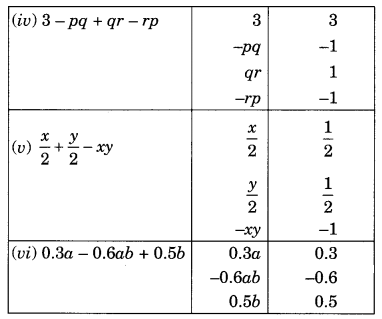
Add the following:
Solution:
(i) Given: ab – bc, bc – ca, ca – ab
We have
(ab – bc) + (bc – ca) + (ca – ab) (Adding all the terms)
= ab – bc + bc – ca + ca – ab
= (ab – ab) + (bc – bc) + (ca – ca) (Collecting the like terms together)
= 0 + 0 + 0
= 0
(ii) Given:
a – b + ab, b – c + bc, c – a + ac
We have (a – b + ab) + (b – c + bc) + (c – a + ac) (Adding all the terms)
= a – b + ab + b – c + bc + c – a + ac
= (a – a) + (b – b) + (c – c) + ab + bc + ac (Collecting all the like terms together)
= 0 + 0 + 0 + ab + bc + ac
= ab + bc + ac
(iii) Given:
2 – 3pq + 4, 5 + 7pq – 3
By arranging the like terms in the same column, we have
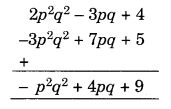
(Adding columnwise)
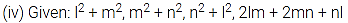
By arranging the like terms in the same column, we have

Thus, the sum of the given expressions is 2( + lm + mn + nl)
Question 4.
(a) Subtract 4a – 7ab + 3b + 12 from 12a – 9ab + 5b – 3
(6) Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + 10xyz
(c) Subtract 4p2q – 3pq + 5pq2 – 8p + 7q – 10 from 18 – 3p – 11q + 5pq – 2pq2 + 5p2q
Solution:
(a) Arranging the like terms column-wise, we have
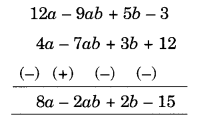
[Change the signs of all the terms of lower expressions and then add]
(b) Arranging the like terms column-wise, we have
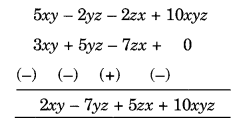
[Change the signs of all the terms of lower expressions and then add]
(c) Arranging the like terms column-wise, we have
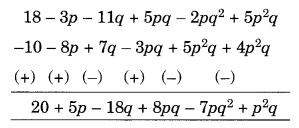
[Change the signs of all the terms of lower expressions and then add]
The terms are p2q – 7pq2 + 8pq – 18q + 5p + 20