Chapter 12 त्रिविमीय ज्यामिति का परिचय Ex 12.2
प्रश्न 1.
निम्नलिखित बिन्दु-युग्मों के बीच की दूरी ज्ञात कीजिए :
(i) (2, 3, 5) और (4, 3, 1)
हल:
दो बिन्दु (x1, y1, z1) और (x2, y2, z2) के बीच की दूरी
बिन्दु (2, 3, 5) और (4, 3, 1) के बीच की दूरी
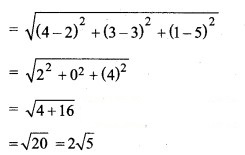
(ii) (- 3, 7, 2) और (2, 4, – 1)
हल:
बिन्दु (-3, 7, 2) और (2, 4, -1) के बीच की दूरी
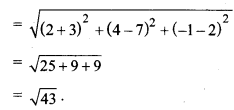
(iii) (- 1, 3, – 4) और (1, – 3, 4)
हल:
बिन्दु (- 1, 3, – 4) और (1, – 3, 4) के बीच की दूरी
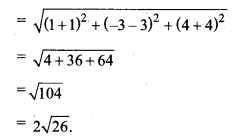
(iv) (2, – 1, 3) और (- 2, 1, 3).
हल:
बिन्दु (2, – 1, 3) और (- 2, 1, 3) के बीच की दूरी
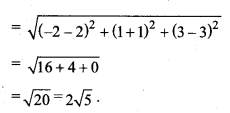
प्रश्न 2.
दर्शाइए कि बिन्दु (- 2, 3, 5), (1, 2, 3) और (7, 0, – 1) सरेख हैं।
हल:
मान लीजिए बिन्दु A(- 2, 3, 5), और B(1, 2, 3) के बीच की दूरी
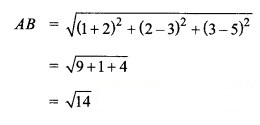
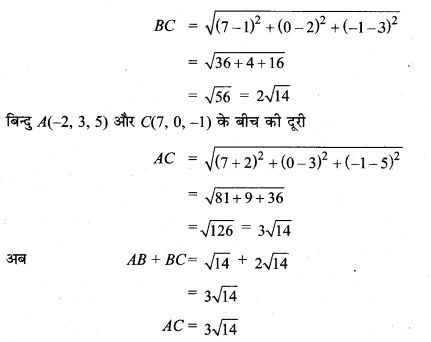
यहाँ AB + BC = AC
अतः बिन्दु A, B, C सरेख हैं।
प्रश्न 3.
निम्नलिखित को सत्यापित कीजिए :
(i) (0, 7, – 10), (1, 6, – 6), और (4, 9, – 6) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
हल:
माना त्रिभुज ABC के शीर्ष A(0, 7, – 10), B(1, 6, – 6) और C(4, 9, – 6) हैं।

अतः दिए गए शीर्ष समद्धिबाहु त्रिभुज के हैं।
(ii) (0, 7, 10), (- 1, 6, 6) और (- 4, 9, 6) एक समकोण त्रिभुज के शीर्ष हैं।
हल:
माना त्रिभुज PQR के शीर्ष P(0, 7, 10), Q(- 1, 6, 6) और R(- 4, 9, 6) हों, तब
PQ2 = (- 1 – 0)2 + (6 – 7)2 + (6 – 10)2
= 1 + 1 + 16 = 18
QR2 = (- 4 + 1)2 + (9 – 6)2 + (6 – 6)2
= 9 + 9 + 0 = 18
PR2 = (- 4 – 0) + (9 – 7) + (6 – 10)2
= 16 + 4 + 16
= 36
PQ2 + QR2 = 18 + 18 = 36
अब PR2 = 36
∴ PQ2 + QR2 = PR2
अतः दिए गए शीर्ष समकोण त्रिभुज के हैं।
(iii) (- 1, 2, 1), (1, – 2, 5), (4, – 7, 8) और (2, – 3, 4) एक समांतर चतुर्भुज के शीर्ष हैं।
हल:
माना चतुर्भुज ABCD के शीर्ष A(- 1, 2, 1), B(1, – 2, 5), C(4, – 7, 8) और D(2, – 3, 4) हों, तब
AB2 = (1 + 1)2 + (- 2 – 2)2 + (5 – 1)2
= 4 + 16 + 16 = 36
BC2 = (4 – 1)2 + (- 7 + 2)2 + (8 – 5)2
= 9 + 25 + 9 = 43
CD2 = (2 – 4)2 + (- 3 + 7)2 + (4 – 8)2
= 4 + 16 + 16 = 36
AD2 = (2 + 1)2 + (- 3 – 2)2 + (4 – 1)2
= 9 + 25 + 9 = 43.
AB2 = CD2 और BC2 = AD2
AB = CD और BC = AD
अतः दिए गए बिन्दु एक समांतर चतुर्भुज के हैं।
प्रश्न 4.
ऐसे बिन्दुओं के समुच्चय का समीकरण ज्ञात कीजिए जो बिन्दु (1, 2, 3) और (3, 2, -1) से समदूरस्थ हैं।
हल:
माना कोई बिन्दु P(x, y, z) बिन्दु A(1, 2, 3) और बिन्दु B(3, 2, – 1) से समान दूरी पर है।
अर्थात् PA = PB
या PA2 = PB2
(x – 1)2 + (y – 2)2 + (z – 3)2 = (x – 3)2+ (y – 2)2 + (z + 1)2
(x2 – 2x + 1) + (z2 – 6z + 9) = (x2 – 6x + 9) + (z2 + 2z + 1)
– 2x + 6x – 6z – 2z + 10 – 10 = 0
या 4x – 8z = 0
अंत: अभीष्ट समीकरण x – 2z = 0.
प्रश्न 5.
बिन्दुओं P से बने समुच्चय का समीकरण ज्ञात कीजिए जिनकी बिन्दुओं A(4, 0, 0) और B(- 4, 0, 0) से दूरियों का योगफल 10 है।
हल:
माना बिन्दु P के निर्देशांक (x, y, z) हैं।
या
दिए गए बिन्दु A(4, 0, 0) और B(- 4, 0, 0) इस प्रकार हैं कि PA + PB = 10
