Chapter 8 त्रिकोणमिति का परिचय Ex 8.4
प्रश्न 1.
त्रिकोणमितीय अनुपातों sin A, sec A और tan A को cot A के पदों में व्यक्त कीजिए।
हल-

प्रश्न 2.
∠A के सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
हल-

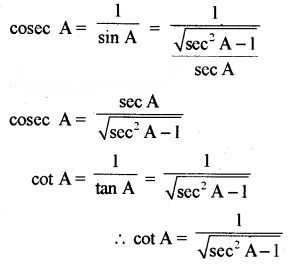
प्रश्न 3.
मान निकालिए-
![]()
हल-

(ii) sin 25° cos 65° + cos 25° sin 65°
हल-
sin 25° cos 65° + cos 25° sin 65°
= sin 25° × cos (90° – 25°) + cos 25° × sin (90° – 25°) [∵ cos(90° – θ) = sin θ, sin(90° – θ) = cos θ]
= sin 25° × sin 25° + cos 25° × cos 25°
= sin2 25° + cos2 25°
= 1
प्रश्न 4.
सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिए :
(i) 9 sec2 A – 9 tan2 A बराबर है :
(A) 1
(B) 9
(C) 8
(D) 0
हल-
9 sec2 A – 9 tan2 A
= 9(sec2 A – tan2 A)
= 9 × 1
= 9
∴ सही विकल्प = (B)
(ii) (1 + tan θ + sec θ) (1 + cot θ – cosec θ) बराबर है :
(A) 0
(B) 1
(C) 2
(D) -1
हल-
(1 + tan θ + sec θ) (1 + cot θ – cosec θ)
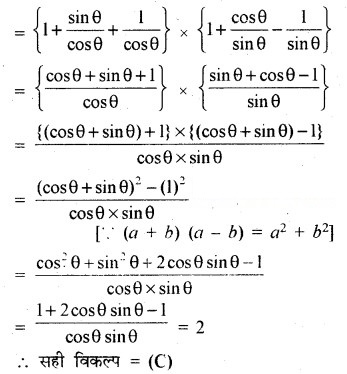
(iii) (sec A + tan A) (1 – sin A) बराबर है :
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
हल-

![]()
(A) sec2 A
(B) -1
(C) cot2 A
(D) tan2 A
हल-

प्रश्न 5.
निम्नलिखित सर्वसमिकाएँ सिद्ध कीजिए जहाँ वे कोण, जिनके लिए व्यंजक परिभाषित है, न्यून कोण हैं :
![]()
हल-



हल-
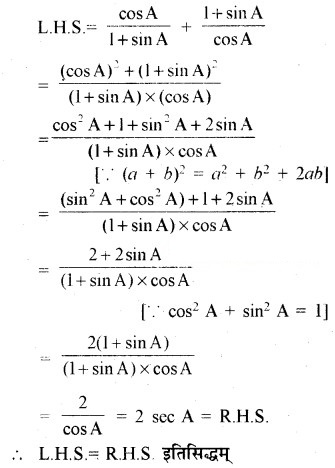

[संकेत: व्यंजक को sin θ और cos θ के पदों में लिखिए]
हल-


![]()
[संकेतः वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए]
हल-
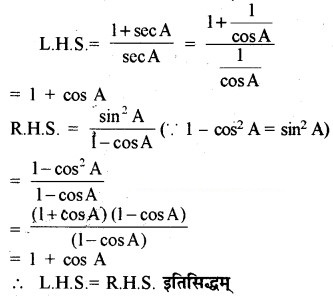

हल-


![]()
हल-

![]()
हल-

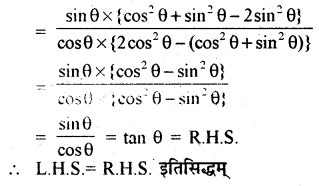
(viii) (sin A + cosec A)2 + (cos A + sec A)2 = 7 + tan2 A + cot2 A
हल-

![]()
[संकेत : वाम पक्ष और दाँया पक्ष को अलग-अलग सरल कीजिए]
हल-


![]()
हल-
