Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.3
जब तक अन्यथा न कहा जाए, π = 22/7 लीजिए।
प्रश्न 1.
त्रिज्या 4.2 cm वाले धातु के एक गोले को पिघलाकर त्रिज्या 6 cm वाले एक बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
हल-
प्रश्नानुसार, गोले की त्रिज्या (r) = 4.2 cm
बेलन की त्रिज्या (R) = 6 cm
मान लो, बेलन की ऊँचाई = H cm
ढालने पर आयतन पहले जितना ही रहता है।
अर्थात् यहाँ गोले का आयतन = बेलन का आयतन
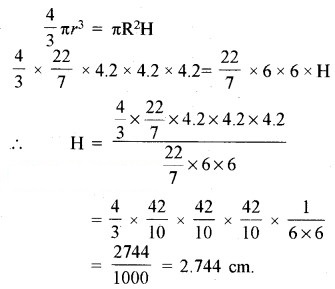
∴ बेलन की ऊँचाई (H) = 2.74 cm
प्रश्न 2.
क्रमशः 6 cm, 8 cm और 10 cm त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
हल-
पहले गोले की त्रिज्या (r1) = 6 cm
दूसरे गोले की त्रिज्या (r2) = 8 cm
तीसरे गोले की त्रिज्या (r3) = 10 cm
माना कि नए बने गोले की त्रिज्या = R cm
तीनों गोलों का आयतन = बड़े गोले का आयतन
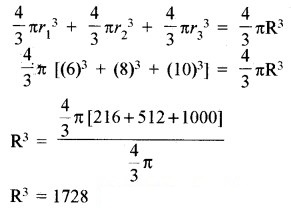
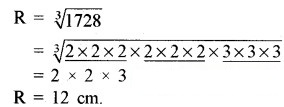
अतः बड़े गोले की त्रिज्या = 12 cm
प्रश्न 3.
व्यास 7 m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 m × 14 m वाला एक चबूतरा बनाया गया है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
हल-
प्रश्नानुसार, कुएँ का व्यास = 7 m
कुएँ (बेलन की त्रिज्या) R = 7272 m
कुएँ की ऊँचाई H1 = 20 m
चबूतरे की लम्बाई (L) = 22 m
चबूतरे की चौड़ाई (B) = 14 m
माना कि चबूतरे की ऊँचाई = H2 m
कुएँ में से निकाली गई मिट्टी का आयतन = बनाए गए चबूतरे का आयतन
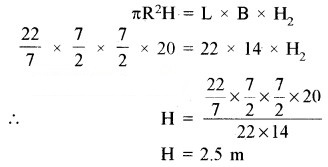
∴ चबूतरे की ऊँचाई (H2) = 2.5 m
प्रश्न 4.
व्यास 3 m का एक कुआँ 14 m की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4 m चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
हल-
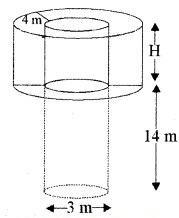
कुएँ की गहराई (h) = 14 m
कुएँ की त्रिज्या (r) = 3/2 m
बांध खोखले बेलन के आकार का है जिसकी आन्तरिक त्रिज्या कुएँ की त्रिज्या के समान है और बाँध की चौड़ाई 4 m है।

= 5.5 m
निकाली हुई, मिट्टी का आयतन = इस प्रकार बने बाँध का आयतन
πr2h = बाह्य बेलन का आयतन – आन्तरिक बेलन का आयतन
πr2h = πR2H – πr2H = πH[R2 – r2]
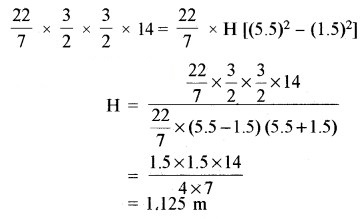
अतः बाँध की ऊँचाई = 1.125 m
प्रश्न 5.
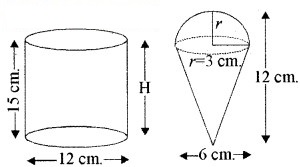
व्यास 12 cm और ऊँचाई 15 cm वाले एक लम्ब वृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम की ऊँचाई 12 cm और व्यास 6 cm वाले शंकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्द्धगोलाकार होगा। उन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं।
हल-
प्रश्नानुसार, बेलन का व्यास (D) = 12 cm
बेलन की त्रिज्या (R) = 6 cm
बेलन की ऊँचाई (H) = 15 cm
शंकु का व्यास = 6 cm
शंकु की त्रिज्या (r) = 3 cm
अर्द्धगोले की त्रिज्या (r) = 3 cm
शंकु की ऊँचाई (h) = 12 cm
माना कि आइसक्रीम भरने के लिए प्रयोग किए गए शंकुओं की संख्या = n
बर्तन में आइसक्रीम का आयतन = n[एक शंकु में आइसक्रीम का आयतन]
πR2H = n[शंकु का आयतन + अर्द्धगोले का आयतन]
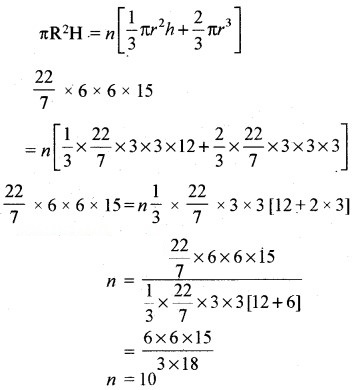
बने शंकुओं की संख्या = 10
प्रश्न 6.
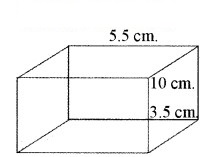
विमाओं 5.5 cm × 10 cm × 3.5 cm वाला एक घनाभ बनाने के लिए 1.75 cm व्यास और 2 mm मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा?
हल-
प्रश्नानुसार, चाँदी का सिक्का बेलन के आकार का है।
∴ चाँदी के सिक्के का व्यास = 1.75 cm
चाँदी के सिक्के की त्रिज्या (r) = 1.75/2
चाँदी के सिक्के की मोटाई = बेलन की ऊँचाई (H) = 2 mm
अर्थात् h = 2/10 cm
घनाभ की लम्बाई (L) = 5.5 cm
घनाभ की चौड़ाई (B) = 10 cm
घनाभ की ऊँचाई (H) = 3.5 cm

माना कि चाँदी के n सिक्कों को पिघला कर नया घनाभ बनाया गया है।
घनाभ का आयतन = n[चाँदी के एक सिक्के का आयतन] = n[πr2h]
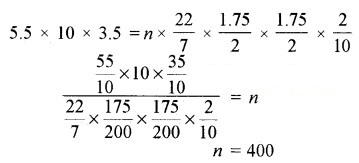
इस प्रकार बने सिक्कों की संख्या = 400
प्रश्न 7.
32 cm ऊँची और आधार त्रिज्या 18 cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदि शंक्वाकार ढेरी की ऊँचाई 24 cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
हल-
प्रश्नानुसार,
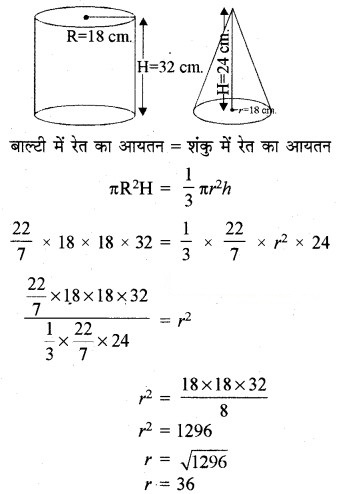
बेलनाकार बाल्टी की त्रिज्या (R) = 18 cm
बेलनाकार बाल्टी की ऊँचाई (H) = 32 cm
शंकु की ऊँचाई (h) = 24 cm
माना कि शंकु की त्रिज्या और तिर्यक ऊँचाई ‘r’ cm और ‘l’ cm है।

प्रश्न 8.
6 m चौड़ी और 1.5 m गहरी एक नहर में पानी 10 km/h की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8 cm गहरे पानी की आवश्यकता होती है।
हल-

प्रश्न 9.
एक किसान अपने खेत में बनी 10 m व्यास वाली और 2 m गहरी एक बेलनाकार टंकी को आन्तरिक व्यास 20 cm वाले एक पाइप द्वारा एक नहर से जोड़ता है। यदि पाइप में पानी 3 km/h की चाल से बह रहा है, तो कितने समय बाद टंकी पूरी भर जाएगी?
हल-
प्रश्नानुसार, पानी की चाल = 3 km/hr
पाइप का व्यास = 20 cm
∴ पाइप की त्रिज्या (r) = 10 cm
= 10/100 m
= 1/10 m
टंकी का व्यास = 10 m
टंकी की त्रिज्या (R) = 5 m
टंकी की गहराई (H) = 2 m
माना कि पाइप n मिनटों में टंकी को भरती है।
टंकी में पानी का आयतन= पाइप द्वारा n मिनटों में बहा पानी
πR2H = n[अन्तःकाट का क्षेत्रफल × पानी की चाल]
πR2H = n[(πr2) × 3 km/h]
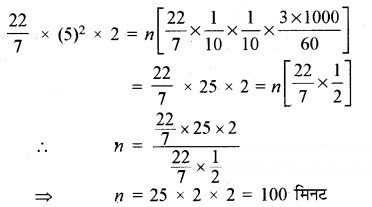
∴ टंकी को भरने में लगा समय = 100 मिनट