Chapter 14 सांख्यिकी Ex 14.3
प्रश्न 1.
निम्नलिखित बारम्बारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।
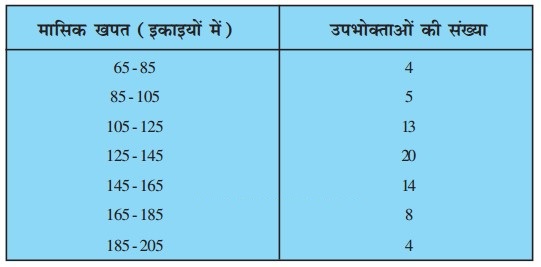
हल-
माध्यक के लिए :
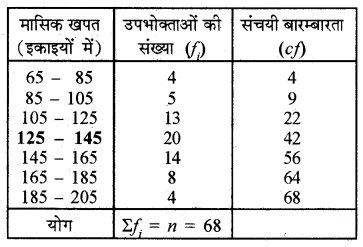
![]()
जो कि वर्ग अन्तराल 125 – 145 में स्थित है।
∴ माध्यक वर्ग = 125 – 145
अतः, l = 125; n = 68; f = 20; cf = 22 और h = 20

![]()
= 125 + 12
= 137 इकाई
माध्य के लिए:
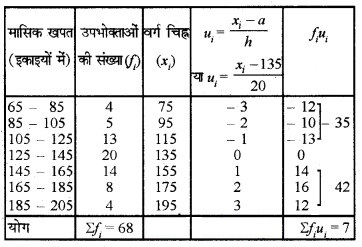
यहाँ कल्पित माध्य (a) = 135 तथा वर्ग माप (h) = 20
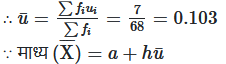
= 135 + 20(0.103)
= 135 + 2.06
= 137.06 इकाई
बहुलक के लिए :
दिए गए आँकड़ों में अधिकतम बारम्बारता 20 है तथा इसके संगत वर्ग 125-145 है।
∴ बहुलक वर्ग = 125 – 145
इसलिए l = 125; f1 = 20; f0 = 13; f2 = 14 और h = 20

अतः, दिए गए आँकड़ों का माध्यक, माध्य और बहुलक है : 137 मात्रक, 137.06 मात्रक और 135.77 मात्रक।
प्रश्न 2.
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो, तो x और y के मान ज्ञात कीजिए :
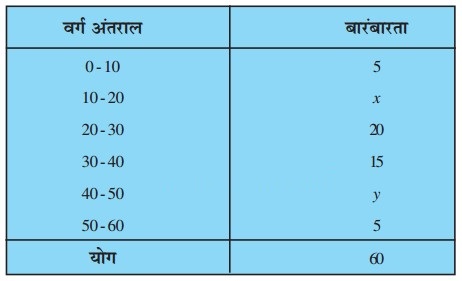
हल-
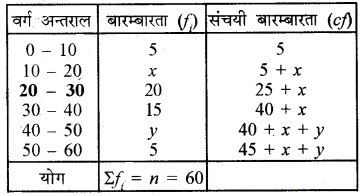
दिए गए आँकड़ों में, Σfi = n = 60
![]()
साथ ही, बंटन का माध्यक = 28.5
जो कि वर्ग अन्तराल 20 – 30 में स्थित है।
∴ माध्यक वर्ग = 20 – 30
इसलिए, l = 20; f = 20; cf = 5 + x; h = 10
सारणी से 45 + x + y = 60
या x + y = 60 – 45 = 15
या x + y = 15 ……(i)

या 57 = 65 – x
या x = 65 – 57 = 8
∴ x = 8
x के इस मान को (i) में प्रतिस्थापित करने पर
8 + y = 15
y = 15 – 8 = 7
अतः, x और y के मान 8 व 7 हैं।
प्रश्न 3.
एक जीवन बीमा एजेंट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्हीं व्यक्तियों को दी जाती है, जिसकी आयु 18 वर्ष या उससे अधिक हो, परन्तु 60 वर्ष से कम हो।
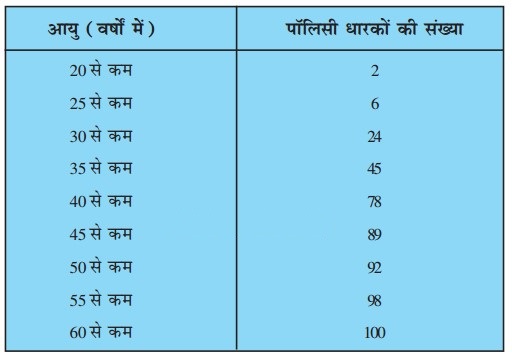
हल-
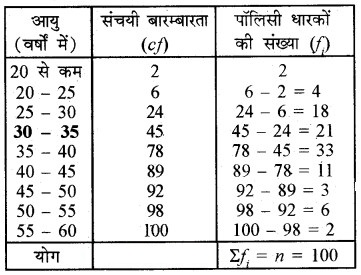
यहाँ, Σfi = n = 100
![]()
जो कि अन्तराल 35 – 40 में स्थित है।
∴ माध्यक वर्ग = 35 – 40
इसलिए, l = 35; n = 100; f = 33; cf = 45 और h = 5

अतः, दिए गए आँकड़ों की माध्यक आयु 35.76 वर्ष है।
प्रश्न 4.
एक पौधे की 40 पत्तियों की लम्बाइयाँ निकटतम मिली मीटरों में मापी जाती हैं तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रूप में निरूपित किया जाता है :
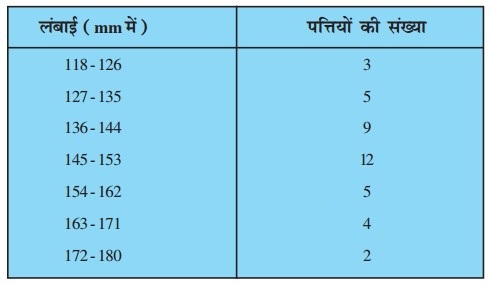
पत्तियों की माध्यक लम्बाई ज्ञात कीजिए।
संकेत : माध्यक ज्ञात करने के लिए आँकड़ों को सतत वर्ग अन्तरालों में बदलना पड़ेगा, क्योंकि सूत्र में वर्ग अन्तरालों को सतत माना गया है। तब ये वर्ग 117.5-126.5, 126.5-135.5, ……, 171.5-180.5 में बदल जाते हैं।
हल-
क्योंकि बारम्बारता बंटन लगातार नहीं है। हम इसे पहले सतत बंटन में परिवर्तित करेंगे :
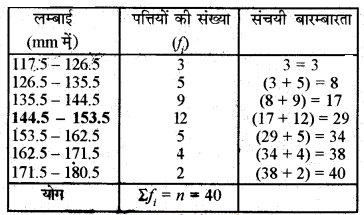
![]()
जो कि अन्तराल 144.5-153.5 में स्थित है।
∴ माध्यक वर्ग = 144.5 – 153.5
इसलिए l = 144.5; f = 12; cf = 17 और h = 9

अतः, पत्तियों की माध्यक लम्बाई 146.75 mm है।
प्रश्न 5.
निम्नलिखित सारणी 400 नियॉन लैंपों के जीवन कालों (life time) को प्रदर्शित करती है :
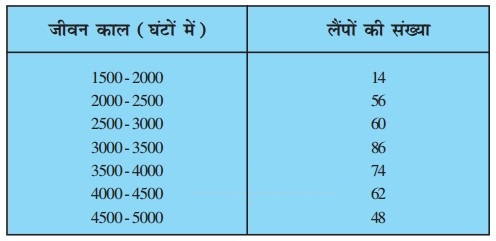
एक लैंप का माध्यक जीवन काल ज्ञात कीजिए।
हल-
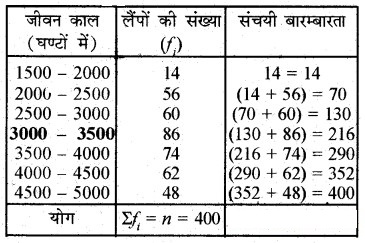
यहाँ, Σfi = n = 400
![]()
जो कि अन्तराल 3000 – 3500 में स्थित है।
∴ माध्यक वर्ग = 3000 – 3500
इसलिए l = 3000; n = 400; f = 86; cf = 130 और h = 500
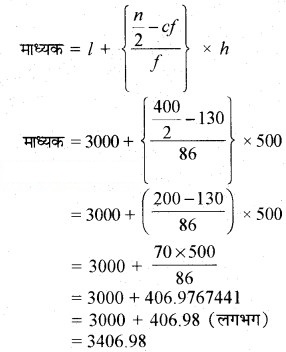
अतः, लैंप का जीवन काल 3406.98 घण्टे है।
प्रश्न 6.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुल नाम (surnames) लिए गए उनमें प्रयुक्त अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारम्बारता बंटन प्राप्त हुआ :

कुल नामों में माध्यक अक्षरों की संख्या ज्ञात कीजिए। कुल नामों में माध्य अक्षरों की संख्या ज्ञात कीजिए। साथ ही, कुल नामों का बहुलक ज्ञात कीजिए।
हल-
माध्यक के लिए :
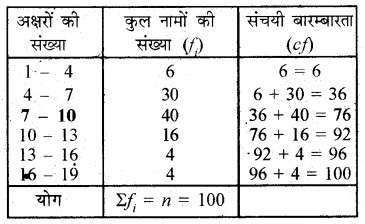
यहाँ, Σfi = n = 100
![]()
जो कि अन्तराल 7-10 में स्थित है।
∴ माध्यक वर्ग = 7-10
इसलिए l = 7; n = 100: f = 40; cf = 36 और h = 3

अतः, माध्यक अक्षरों की संख्या 8.05 है।
माध्य के लिए:
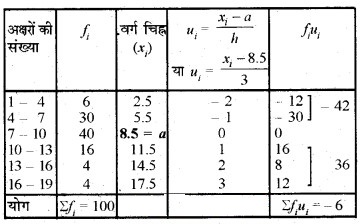
यहाँ कल्पित माध्य (a) = 8.5 तथा वर्ग माप (h) = 3
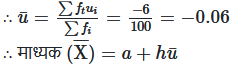
= 8.5 + 3 (-0.06)
= 8.5 – 0.18
= 8.32
अतः, कुल नामों में माध्य अक्षरों की संख्या 8.32 अक्षर है।
बहुलक के लिए :
दिए गए आँकड़ों में अधिकतम बारम्बारता 40 है तथा इसका संगत अन्तराल 7-10 है।
∴ बहुलक वर्ग = 7-10
इसलिए l = 7; f1 = 40; f0 = 30; f2 = 16 और h = 3

अतः, कुल नामी का बहुलक माप 7.88 अक्षर है।
प्रश्न 7.
नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए:

हल-
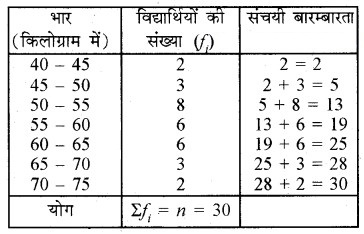
यहाँ, Σfi = n = 30
![]()
जो कि अन्तराल 55-60 में स्थित है।
∴ माध्यक वर्ग = 55-60
इसलिए l = 55; n = 30; f = 6; cf = 13 और h = 5
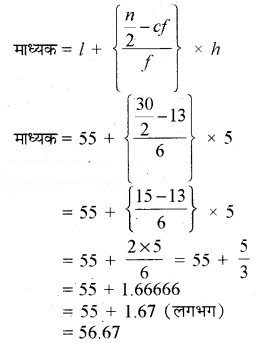
अतः, माध्यक भार 56.67 किलोग्राम है।