Chapter 1 संख्या पद्धति Ex 1.3
प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक का दशमलव प्रसार किस प्रकार का है
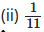
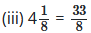
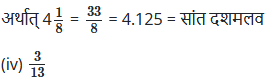
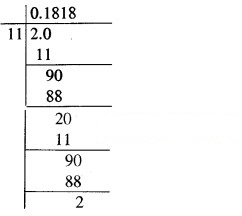
या x= 0.6666 ………..(i)
दोनों पक्षों में 10 का गुणा करने पर
10x = 10 × (0.6666…) = 6.6666 ….
⇒ 10x = 6.6666……….(ii)
समीकरण (ii) में से (i) को घटाने पर
10x – x = (6.6666…..) – (0.6666)
या 9x = 6
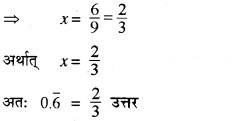
प्रश्न 4.
0.9999….. को p/q के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं ? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।
हल:
माना कि x = 0.9999 ………(i)
दोनों पक्षों में 10 से गुणा करने पर
10x = 10 × (0.99999…..)
10x = 9.9999 ……….(ii)
समीकरण (ii) में से (i) को घटाने पर
10x – x = (9.9999….) – (0.9999….)
⇒ 9x = 9
⇒ x = 9/9 = 1
अतः 0.99999….. = 1
हाँ। हम उत्तर से आश्चर्यचकित हैं। परन्तु उत्तर सार्थक है क्योंकि प्रश्नानुसार हम देखते हैं कि 0.9999….. सतत है अर्थात् दशमलव के बाद 9 का अंक लगातार आएगा। अर्थात् 1 और 0.9999 के बीच कोई रिक्तता या शून्यता नहीं है। अत: वे समान हैं।
प्रश्न 5.
\frac{1}{17} के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन क्रिया कीजिए।
हल:
यहाँ शेष 1 रहने पर चरण B अर्थात् आगे का हल प्रथम चरण A के अनुसार है।
प्रश्न 6.
p/q (q ≠ 0) के रूप की परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि 4 को कौनसा गुण अवश्य सन्तुष्ट करना चाहिए?
हल:
आदि हो सकती हैं जिनका सात दशमलव निरूपण होता है। सात दशमलव की परिभाषा के अनुसार जब किसी परिमेय संख्या का हर 2 या 5 या दोनों की घात में हो तो ऐसी परिमेय संख्याओं से सांत दशमलव प्राप्त होता है। अन्य शब्दों में यह भी कहा जा सकता है कि परिमेय संख्या \frac{p}{q} (q ≠ 0) को सांत दशमलव रूप में निरूपित करने के लिए यह आवश्यक है कि प्रत्येक ऐसा लिया जाए कि के अभाज्य गुणनखण्ड में केवल 2 के घात या 5 के घात या दोनों ही हों।
प्रश्न 7.
ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हों।
हल:
हम जानते हैं कि एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी अनावर्ती होता है या इसका विलोम अर्थात् वह संख्या जिसका दशमलव प्रसार अनवसानी अनावर्ती होता है, अपरिमेय होती है।
अतः √2 = 1.41421356237 …..
√3 = 1.73205080756 …..
√10 = 3.16227766016 …..
इन उदाहरणों के अतिरिक्त छात्र स्वयं भी कुछ अन्य अपरिमेय या ऐसी संख्याएँ लिख सकते हैं जिनके दशमलव प्रसार अनवसानी हों। जैसे
0.01001000100001……,
0.202002000200002…..,
0.003000300003….. आदि।
प्रश्न 8.
परिमेय संख्याओं में 5/7 और 9/11 के बीच की = तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।
हल:
परिमेय संख्या \frac{5}{7} का दशमलव निरूपण निम्नानुसार है-
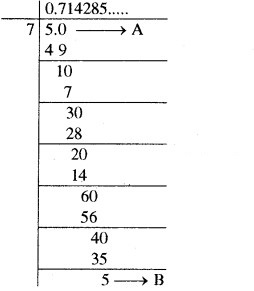
इसके आगे हल करने की प्रक्रिया पूर्वानुसार है।
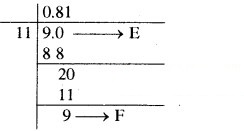
प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौन-कौन संख्याएँ परिमेय और कौन-कौन संख्याएँ अपरिमेय हैं
(i) √23
(ii) √225
(iii) 0.3796
(iv) 7.478478…..
(v) 1.101001000100001…..
हल:
अपरिमेय संख्याएँ-(i) व (v) हैं।
(i) √23 अभाज्य संख्या होने के कारण अपरिमेय है क्योंकि अभाज्य संख्या एक पूर्ण वर्ग संख्या नहीं होती है।
(v) 1.101001000100001….. यह संख्या अपरिमेय संख्या है क्योंकि दशमलव प्रसार अनवसानी अनावर्ती है।
परिमेय संख्याएँ-(ii), (iii) व (iv) हैं।
(iii) 0.3796 का दशमलव प्रसार सांत दशमलव होने के कारण परिमेय संख्या है।
(iv) 7.478478…. का दशमलव प्रसार अनवसानी आवर्ती होने के कारण एक परिमेय संख्या है।