Chapter 12 हीरोन का सूत्र Ex 12.2
प्रश्न 1.
एक पार्क चतुर्भुज ABCD के आकार का है, जिसमें ∠C = 90°, AB = 9 m, BC = 12 m, CD = 5 m और AD = 8 m है। इस पार्क का कितना क्षेत्रफल है?
हल:
प्रश्नानुसार दी गई मापों के आधार पर चतुर्भुजाकार पार्क का चित्र बनाया तथा बिन्दु B को D से मिलाने पर यह आकृति दो त्रिभुजाकार आकृतियों ∆BCD तथा ∆ABD में विभाजित हो गई।

अब ∆BCD का क्षेत्रफल

= 30 m2 ……. (i)
समकोण ∆BCD में
BD2 = CD2 + BC2
= (5)2 + (12)2
= 25 + 144 = 169
∴ BD = √169 = 13 m
अर्थात् भुजा BD = 13 m
अब ∆ABD में AB = 9 m, BD = 13 m तथा AD = 8 m
हीरोन के सूत्रानुसार ∆ ABD का क्षेत्रफल

अब पूरे चतुर्भुजाकार पार्क का क्षेत्रफल
= ar(∆BCD) + ar(∆ABD)
= 30 m2 + 35.5 m2
= 65.5 m2
प्रश्न 2.
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 3 cm, BC = 4 cm; CD = 4 cm, DA = 5 cm और AC 35 cm है।
हल:
प्रश्नानुसार चतुर्भुजाकार आकृति का चित्र बनाने पर हम देखते हैं कि ये आकृति दो त्रिभुजों क्रमशः ∆ABC तथा ∆ACD में विभक्त है।

∆ABC के क्षेत्रफल के लिए अर्द्ध-परिमाप (s)


∴ सम्पूर्ण चतुर्भुज का क्षेत्रफल
= ar (∆ABC) + ar(∆ACD)
= 6 cm2 + 9.2 cm2
= 15.2 cm2
प्रश्न 3.
राधा ने एक रंगीन कागज से एक हवाई जहाज का चित्र बनाया, जैसा कि आकृति में दिखाया गया है। प्रयोग किए गए कागज का कुल क्षेत्रफल ज्ञात कीजिए।

हल:
चित्रानुसार दी गई आकृति पाँच भागों में विभाजित है। अतः सम्पूर्ण क्षेत्रफल ज्ञात करने के लिए अलग-अलग भागों का क्षेत्रफल ज्ञात करके योग करना होगा।
भाग I का क्षेत्रफल-यह एक समद्विबाहु त्रिभुज के आकार की आकृति है जिसकी भुजाएँ 5 cm, 5 cm तथा 1 cm हैं । अतः

भाग II का क्षेत्रफल-यह आकृति आयताकार है जिसकी लम्बाई 6.5 cm तथा चौड़ाई 1 cm है। अतः
क्षेत्रफल = 6.5 × 1 = 6.5 cm2 …. (ii)
भाग III का क्षेत्रफल-इसमें समान्तर भुजाएँ 2 cm व I cm हैं और बराबर भुजाओं में से प्रत्येक 1 cm है।

2 cm की भुजा के मध्य बिन्दु से ऊपर की समान्तर भुजाओं को जोड़कर आकृति को 1 cm भुजा वाले 3 समबाहु त्रिभुजों में विभक्त किया गया है, तब आकृति III का क्षेत्रफल

∴ राधा द्वारा प्रयुक्त किए गए कागज का कुल क्षेत्रफल = भाग I का क्षेत्रफल + भाग II का क्षेत्रफल + भाग III का क्षेत्रफल + भाग IV व भाग V का क्षेत्रफल
= (2.5 + 6.5 + 1.3 + 4.5 + 4.5) cm
= 19.3 cm2
अत: पूरी आकृति का क्षेत्रफल = 19.3 cm2
प्रश्न 4.
एक त्रिभुज और एक समान्तर चतुर्भुज का एक ही आधार है और क्षेत्रफल भी एक ही है। यदि त्रिभुज की भुजाएँ 26 cm, 28 cm और 30 cm हैं तथा समान्तर चतुर्भुज 28 cm के आधार पर स्थित है, तो उसकी संगत ऊँचाई ज्ञात कीजिए।
हल:
प्रश्नानुसार दिया गया है कि त्रिभुज तथा समान्तर चतुर्भुज का क्षेत्रफल समान है। अब ∆ ABE का क्षेत्रफल ज्ञात करते हैं।


अब हीरोन के सूत्र से क्षेत्रफल

हम जानते हैं कि समान्तर चतुर्भुज का क्षेत्रफल
= आधार × संगत ऊँचाई
अतः संगत ऊँचाई
![]()
संगत चौड़ाई = 12 cm
अतः समान्तर चतुर्भुज की संगत ऊँचाई = 12 सेमी.
प्रश्न 5.
एक समचतुर्भुजाकार घास के खेत में 18 गायों के चरने के लिए घास है। यदि इस समचतुर्भुज की प्रत्येक भुजा 30 m है और बड़ा विकर्ण 48 m है, तो प्रत्येक गाय को चरने के लिए इस घास के खेत का कितना क्षेत्रफल प्राप्त होगा?
हल:
माना कि समचतुर्भुजाकार खेत ABCD है। इसकी प्रश्नानुसार प्रत्येक भुजा AB = BC = CD = DA = 30 m तथा विकर्ण AC = 48 m है। विकर्ण AC इस आकृति को दो सर्वांगसम त्रिभुजों क्रमश: ∆ABC तथा ∆ADC में बाँटता है। हम यह भी जानते हैं कि सर्वांगसम त्रिभुज क्षेत्रफल में समान होते हैं।

अब ∆ABC का क्षेत्रफल ज्ञात करेंगे।
अर्द्ध-परिमाप = 30+30+48230+30+482 = 10821082 = 54 m
हीरोन के सूत्रानुसार क्षेत्रफल

= 2 × 2 × 2 × 2 × 3 × 3 × 3 m2
= 16 × 27 m2
= 432 m2
अतः समचतुर्भुज ABCD का क्षेत्रफल
= ar(∆ABC) + ar(∆ADC)
= 432 + 432
= 864 m2
∵ 18 गायों के लिए चरने का कुल क्षेत्रफल
= 864 m2
∴1 गाय के लिए चरने का क्षेत्रफल
= 864
= 48 m2
प्रश्न 6.
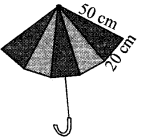
दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों को सीकर एक छाता बनाया गया है ( देखिए आकृति)। प्रत्येक टुकड़े के माप 20 cm, 50 cm और 50 cm हैं। छाते में प्रत्येक रंग का कितना कपड़ा लगा है?
हल:
प्रश्नानुसार दो विभिन्न रंगों के कपड़ों के 10 त्रिभुजाकार टुकड़ों में से प्रत्येक टुकड़े की माप क्रमशः 20 cm, 50 cm तथा 50 cm है। अर्थात् ये टुकड़े समद्विभुजाकार त्रिभुज के हैं। अतः
एक टुकड़े का अर्द्ध-परिमाप
![]()
त्रिभुज का क्षेत्रफल ज्ञात करने के हीरोन के सूत्रानुसार क्षेत्रफल

यदि यह मान लिया जाए कि छाते में लगे दो रंग लाल एवं पीला हैं तो एक छाते में प्रत्येक रंग के 5-5 टुकड़े होंगे। अर्थात् लाल रंग के कपड़े का कुल क्षेत्रफल
= 5 × 200√6 cm
= 1000√6 cm2
तथा पीले रंग के कपड़े का कुल क्षेत्रफल .
= 5 × 200√6 cm2
= 1000√6 cm2
प्रश्न 7.
एक पतंग तीन भिन्न-भिन्न शेडों (shades) के कागजों से बनी है। इन्हें आकृति में I, II और III से दर्शाया गया है। पतंग का ऊपरी भाग 32 cm विकर्ण का एक वर्ग है और निचला भाग 6 cm, 6 cm और 8 cm भुजाओं का 6 cmx6 cm एक समद्विबाहु त्रिभुज है। ज्ञात 8 cm कीजिए कि प्रत्येक शेड का कितना कागज प्रयुक्त किया गया है।

हल:
प्रश्न एवं आकृति के अनुसार शेड I + शेड II का क्षेत्रफल समान होगा। अतः शेड I का क्षेत्रफल अर्थात् समकोण त्रिभुज का क्षेत्रफल
= 1/2 × 32 × 16 cm2
= 256 cm 2
अतः शेड I का क्षेत्रफल = शेड II का क्षेत्रफल
= 256 cm2
शेड III के क्षेत्रफल के लिए

प्रश्न 8.
फर्श पर फूलों का एक डिजाइन 16 त्रिभुजाकार टाइलों से बनाया गया है, जिनमें से प्रत्येक की भुजाएँ 9 cm, 28 cm और 35 cm हैं ( देखिए आकृति)। इन टाइलों को 50 पैसे प्रति cm2 की दर से पालिश कराने का व्यय ज्ञात कीजिए।

हल:
प्रश्नानुसार त्रिभुजाकार टाइलों की भुजाएँ क्रमशः 9 cm, 28 cm तथा 35 cm हैं । अतः
![]()
अब त्रिभुजाकार टाइल का क्षेत्रफल हीरोन के सूत्रानुसार

∴ 16 टाइलों का क्षेत्रफल = 16 × 36√6
= 576√6
∵ 1 cm को पॉलिश कराने का खर्चा
= 50 पैसे = 1/2 रु.
∴ 575√6 cm2 को पॉलिश कराने का खर्चा
= 1/2 × 576√6
= 288√6
= 288 × 2.45
= 705.60 रु.
अत: टाइलों पर पॉलिश कराने का व्यय
= 705.60 रु.
प्रश्न 9.
एक खेत समलम्ब के आकार का है जिसकी समान्तर भुजाएँ 25 m और 10 m हैं। इसकी असमान्तर भुजाएँ 14 m और 13 m हैं। इस खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
प्रश्नानुसार माना कि PQRS एक समलम्ब चतुर्भुज है जिसमें PQ || SR तथा SR = 10 m, PQ = 25 m, SP = 13 m, RQ = 14 m

अब RT || SP खींची और SR || PQ दिया है।
∴ RT = SP = 13 m
क्योंकि समान्तर चतुर्भुज की सम्मुख भुजाएँ समान होती हैं।
तथा TQ = 25 m – 10 m = 15 m
अब RU ⊥ TQ खींचा।
∆ RTQ की भुजाएँ क्रमश: 15 m, 14 m तथा 13 m हैं।
अर्द्ध-परिमाप (s) = 15 +14+13 = 42 = 21 m
हीरोन के सूत्र के अनुसार क्षेत्रफल

अब RU = 2×84152×8415 m = 565565 m
![]()
अतः समलम्ब PQRS का क्षेत्रफल
= समान्तर चतुर्भुज SRPT का क्षेत्रफल + ∆RTQ का क्षेत्रफल
= [10 × 565565 + 84]m2
= (112 + 84) m2
= 196 m2