Chapter 1 पूर्णांक Ex 1.3
प्रश्न 1.
निम्नलिखित गुणनफलों को ज्ञात कीजिए :
(a) 3 x (-1)
(b) (-1) x 225
(c) (-21) x (-30)
(d) (-316) x (-1)
(e) (-15) x 0 x (-18)
(f) (-12) x (-11) x 10
(g) 9 x (-3) x (-6)
(h) (-18) – (-5) (-4)
(i) (-1) (-2) (-3) x 4
(j) (-3)x (-6) (-2) x (-1)
हल:
(a) 3 x (-1) = – (3 x 1) = -3
(b) (-1) x 225 = – (1 x 225) = – 225
(c) (-21) x (-30) = + (21 x 30)
= [(20+ 1) x 30] = 20 x 30+ 1 x 30
= 600 + 30 = 630
(d)(-316) x (-1) = + (316 x 1)= 316
(e) (-15) x 0 x (- 18)
= [(- 15) x 0] x (-18)
= 0 x (-18) = 0
(f) (-12) x (-11) x 10
= + [(12 x 11) x 10]
= 132 x 10 = 1320 उत्तर
(∵ ऋणात्मक पूर्णांकों की सम संख्याओं का गुणनफल धनात्मक होता है)
(g) 9x (-3) x (-6) = + (9 x 3 x 6) = 162
(h) (-18) x (-5) x (-4) = -(18 x 5 x 4) = -360 (∵ ऋणात्मक पूर्णांकों की विषम संख्याओं का गुणनफल ऋणत्मक होता है)
(i) (-1)- (-2) x (-3) x 4 = – (1 x 2 x 3 x 4)= – 24
(j) (-3) x (-6) x (-2) (-1) = + (3 x 6 x 2 x 1) = 36
प्रश्न 2.
निम्नलिखित को सत्यापित कीजिए :
(a) 18 x [7 + (-3)] = [18 x 7] + [18x (-3)]
(b) (-21) x [(-4)+ (-6)] = [(-21) x (-4)] + [(-21) x (-6)]
हल:
(a) 18 x [7 + (-3)] = (18×7) + [18 – (-3)]
L.H.S. = 18 – [7 + (-3)]
= 18 x (7 – 3)
= 18 x 4 = 72
R.H.S. = [18 x 7] + [18x (-3)]
= 126 + (-54) = 126 – 54 = 72
∵L.H.S. = R.H.S.
∴ 18 x [7 + (-3)] = [18 x 7] + [18 x (-3)]
(b) (-21)x [(-4)+ (-6)] = [(-21) x (-4)] + [(-21)x (-6)]
L.H.S. = (-21) [(-4) + (-6)]
= (-21) x (-10)
=+ (21 x 10) = 210
R.H.S. = [(-21) x (-4)] + [(-21)- (-6)]
= (+ 84) + (+ 126)
= 84 + 126 = 210
∵L.H.S. = R.H.S.
∴ (-21) x [(-4) + (-6)] = [(-21)x (-4)+ [(-21)- (-6)]
प्रश्न 3.
(i) किसी भी पूर्णांक a के लिए, (-1) x a किसके समान है ?
(ii) वह पूर्णांक ज्ञात कीजिए, जिसका (-1) के साथ गुणनफल है :
(a) -22
(b) 37
(c) 0
हल:
(i) (-1) x a = -a
(ii) ∵ (- 1) x (कोई पूर्णांक) = पूर्णांक का योज्य प्रतिलोम
अतः (a) (-1) x 22 = – 22
(b) (-1) (-37) = 37
(c) (-1) x 0 = 0
प्रश्न 4.
(-1) x 5 से प्रारम्भ करके विभिन्न गुणनफलों द्वारा कोई पैटर्न दर्शाते हुए (-1) x (-1)= 1 को निरूपित कीजिए।
हल:
∵(-1) x 5 = -5
(-1) x 4 = – 4 = (-5) + 1
(-1) x 3 = -3 = (-4) + 1
(-1) x 2 = – 2 = (-3) + 1
(-1) x 1 = – 1 = (-2) + 1
(-1) x 0 = 0 = (-1) + 1
(-1) x (-1)= 1 = 0 + 1
प्रश्न 5.
उचित गुणों का उपयोग करते हुए, गुणनफल ज्ञात कीजिए-
(a) 26 x (-48) + (-48) x (-36)
(b) 8 x 53 x (-125)
(c) 15 x (-25) x (-4)x (-10)
(d) (-41) x 102
(e) 625 – (-35) + (-625) x 65
(f) 7 x (50 – 2)
(g) (-17) x (-29)
(h) (-57) x (-19) + 57
हल:
(a) 26 x (-48) + (-48) x (-36)
= (-48) [26 + (-36)] (योग पर गुणन का वितरण नियम)
= (-48) (- 10) = 480
(b) 8 x 53 x (-125)
= 8 x (-125) x 53 (गुणन का साहचर्य नियम)
= (- 1000) x 53 = -53000
(c) 15 x (-25) x (-4) x (- 10) = [(-25) x (-4)] – [(-10) x 15] (गुणन का साहचर्य नियम)
= [(100) x (- 150)] = -(100 x 150)
= -15000
(d) (-41) x (102)
= (-41)x (100 + 2) (योग पर गुणन का वितरण नियम)
= (-41) x 100 + (-41) x 2
= – 4100 + (-82)= – 4182
(e) 625 x (-35) + (-625) x 65
= 625 [(-35) + (-65)]
= 625 x (- 100) = – 62500
(f) 7 x (50 – 2)
= 7 x 50 – 7 x 2 [∵ a x (b – c) = a x b – a x c]
=350 – 14 = 336
(g) (-17) – (-29)
= + (17 x 29)
= 17 x (30 – 1) [∵ a x (b – c) = a x b – a x c]
= 510 – 17
= 493
(h) (-57) x (-19) + 57
= (-57) x (-19) + [(-57) x (-1)]
= (-57) x [(-19) + (-1)]
= (-57) x (-20)
= 57 x 20
= 1140
प्रश्न 6.
किसी हिमीकरण (ठण्डा) प्रक्रिया में, कमरे के तापमान को 40°C से, 5°C प्रति घण्टे की दर से कम करने की आवश्यकता है। इस प्रक्रिया के शुरू होने के 10 घण्टे बाद कमरे का तापमान क्या होगा?
हल:
कमरे का तापमान = 40°C
प्रति घण्टा तापमान में कमी = -5°C
∴ 10 घण्टे में तापमान कम होगा = (-5) x 10 °C = -50°C
∴ 10 घण्टे बाद कमरे का तापमान = 40°C – 50°C = – 10°C
प्रश्न 7.
दस प्रश्नों वाले एक कक्षा टेस्ट में प्रत्येक सही उत्तर के लिए 5 अंक दिये जाते हैं और प्रत्येक गलत उत्तर के लिए (-2) अंक दिए जाते हैं एवं प्रयत्न नहीं किए गए प्रश्नों के लिए शून्य अंक दिया जाता है।
(i) मोहन चार प्रश्नों का सही और छः प्रश्नों का गलत . उत्तर देता है। उसके द्वारा प्राप्त अंक कितने हैं ?
(ii) रेश्मा के पाँच उत्तर सही हैं और पाँच उत्तर गलत हैं। उसके द्वारा प्राप्त अंक कितने हैं ?
(iii) हीना ने कुल सात प्रश्न किए हैं। उनमें से दो का उत्तर सही है और पाँच का उत्तर गलत है, तो उसे कितने अंक प्राप्त होते हैं ?
हल:
कुल प्रश्नों की संख्या = 10
सही उत्तर के लिए अंक = 5
गलत उत्तर के लिए अंक = -2
प्रयत्न न किए गए प्रश्नों के लिए अंक = 0
(i) मोहन के अंक = 4 x 5 + 6 x (-2)
= 20 – 12 = 8
(ii) रेश्मा के अंक = 5 x 5 + 5 x (-2)
= 25 + (-10)
= 25-10 = 15
(iii) हीना के अंक = 2 x 5 + 5 x (-2) + 3 x 0
= 10 + (-10) + 0
= 10 – 10 + 0 = 0
प्रश्न 8.
एक सीमेंट कम्पनी को सफेद सीमेंट बेचने पर ₹ 8 प्रति बोरी की दर से लाभ होता है तथा स्लेटी (Grey) रंग की सीमेंट बेचने पर ₹ 5 प्रति बोरी की दर से हानि होती है।
(a) किसी महीने में वह कम्पनी 3000 बोरियाँ सफेद सीमेंट की और 5000 बोरियाँ स्लेटी सीमेंट की बेचती है। उसका लाभ अथवा हानि क्या है ?
(b) यदि बेची गई स्लेटी सीमेंट की बोरियों की संख्या 6400 है, तो कम्पनी को सफेद सीमेंट की कितनी बोरियाँ बेचनी चाहिए, ताकि उसे न तो लाभ हो और न ही हानि ?
हल:
सफेद सीमेंट की प्रति बोरी पर लाभ = ₹ 8
स्लेटी सीमेंट की प्रति बोरी पर हानि = ₹ 5
(a) सफेद सीमेंट की बेची गईं बोरियों की संख्या = 3000
स्लेटी सीमेंट की बेची गईं बोरियों की संख्या = 5000
∴ लाभ = 3000 x ₹ 8 = ₹ 24000
व, हानि = 5000 x ₹ 5 =₹ 25000
यहाँ, लाभ से हानि अधिक है।
अतएव, हानि = ₹ 25000 – ₹ 24000
= ₹ 1000
(b) स्लेटी सीमेंट की बेची गई बोरियों की संख्या = 6400
कुल हानि = ₹ 6400 x 5
= ₹ 32000
उसे न तो लाभ हो और न ही हानि के लिए ₹ 32000 का लाभ होना चाहिए।
∴ ₹ 32000 लाभ के लिए उसे सफेद सीमेंट की बोरियाँ बेचनी चाहिए = 32000 ÷ 8
= 4000 बोरियाँ
प्रश्न 9.
निम्न को सत्य कथन में परिवर्तित करने के लिए, रिक्त स्थान को एक पूर्णांक में प्रतिस्थापित कीजिए
हल:
(a) (-3) x (-9) = 27
(b) 5 x (-7) = -35
(c) 7 x (-8) = -56
(d) (-11) x (-12) = 132
पाठ्य-पुस्तक पृष्ठ संख्या # 23
पूर्णांकों का विभाजन
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए।
हल:
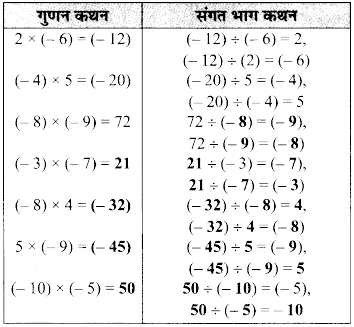
अतः हम गुणन कथन तथा संगत भाग कथन को लिख सकते हैं।
प्रयास कीजिए
प्रश्न 1.
ज्ञात कीजिए-
(a) (-100) ÷ 5.
(b) (-81) ÷ 9
(c)(-75) ÷ 5
(d) (-32) ÷ 2
हल:
जब हम ऋणात्मक पूर्णांक को धनात्मक पूर्णांक से भाग देते हैं, तो पूर्णांक संख्याओं में भाग देकर भागफल से पहले ऋण चिह्न लगा देते हैं।
(a) ∴ (-100) ÷ 5 = (-20)
(b) ∴ (-81) ÷ 9 = -9
(c) ∴ (-75) ÷ 5 = (-15)
(d) ∴ (-32) ÷ 2 = (-16)
पाठ्य-पुस्तक पृष्ठ संख्या # 24
प्रयास कीजिए
प्रश्न 1.
ज्ञात कीजिए-
(a) 125 ÷ (-25)
(b) 80 ÷ (-5)
(c) 64 ÷ (-16)
हल:
जब हम धनात्मक पूर्णांक को ऋणात्मक पूर्णांक से भाग देते हैं, तो पूर्णांक संख्याओं में भाग देकर भागफल से पहले ऋण चिह्न लगा देते हैं।
(a) ∴ 125 ÷ (-25) = (-5)
(b) ∴ 80 ÷ (-5) = -16
(c) ∴ 64 ÷ (-16) = (-4)
प्रश्न 2.
ज्ञात कीजिए
(a) ∴ (-36) ÷ (-4)
(b) ∴ (-201) ÷ (-3)
(c) ∴ (-325) ÷ (-13)
हल:
जब एक ऋणात्मक पूर्णांक को एक ऋणात्मक पूर्णांक से भाग देते हैं तो सर्वप्रथम हम उन्हें पूर्ण संख्याओं के रूप में भाग देते हैं और उसके पश्चात् भागफल से पहले धनात्मक चिह्न (+) लगा देते हैं।
(a) ∴ (-36) ÷ (-4) = 36 ÷ 4 = +9
(b) ∴ (-201) ÷ (-3) = 201 ÷ 3 = + 67
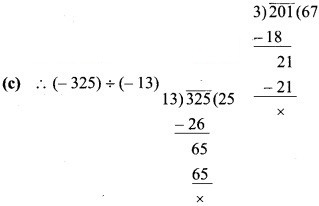
= 325 : 13 = + 25
पूर्णांकों के भाग के गुण
निम्नलिखित सारणी को देखिए और इसे पूरा कीजिए।
हल:
कथन

अतः पूर्णांक भाग के अन्तर्गत संवृत नहीं है।
पाँच और उदाहरण लेते हुए, इस कथन की सत्यता के लिए उचित कारण बताइए।
उदाहरण:

अत: भागफल सदैव पूर्णांक प्राप्त नहीं होता।
पाठ्य-पुस्तक पृष्ठ संख्या # 25
भाग में पूर्णांकों के लिए क्रम-विनिमेय नियम नहीं है। पाँच और उदाहरण लेकर इसे सत्यापित कीजिए :
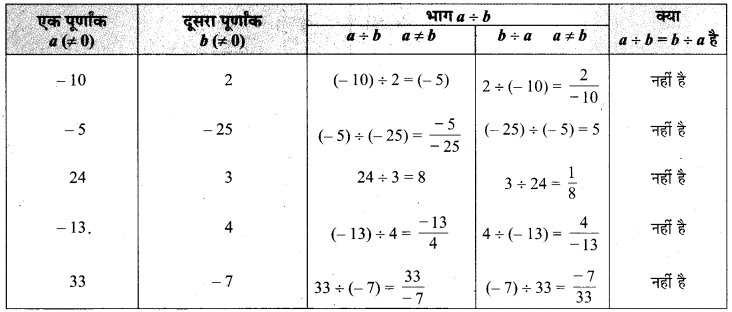
अतः स्पष्ट है कि पूर्णांकों के लिए भाग क्रम-विनिमेय नहीं है।
निम्नलिखित को देखिए-
हल:
किसी पूर्णांक को 1 से भाग देने पर वही पूर्ण संख्या प्राप्त होती है।
(i) ∴ (-25) ÷ 1 = (-25)
(ii) ∴ (-37) ÷ 1 = – 37
(ii) ∴ (-48) ÷ 1 = (-48)
निम्नलिखित सारणी को पूरा कीजिए-
हल:
किसी पूर्णांक को (-1) से भाग देने पर वही पूर्णांक प्राप्त नहीं होता है।
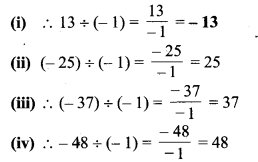
किसी संख्या के लिए भाग साहचर्य है/नहीं। अपनी ओर से पाँच उदाहरण लेकर इसे सत्यापित कीजिए।
उदाहरण:
(i) [24 ÷ 6] ÷ (-2) और (-24) ÷ [6 ÷ (-2)]
[(-24) ÷ 6] ÷ (-2) = (-4) ÷ (-2) = 2
और (-24) ÷ [6 ÷ (-2)] = (-24) ÷ (-3) = 8
अतः [(-24) ÷ 6] + (-2) ÷ (-24) ÷ [6 + (-2)]
(ii) (15 ÷ 3) ÷ 5 और 15 ÷ (3 ÷ 5)
∴ (15 ÷ 3) + 5 = 5 + 5 = 1
और 15 F = 2 =
अतः (15 ÷ 3) ÷ 5 ≠ 15 ÷ ( 3 ÷ 5)
(iii) [(-36) ÷ (-4)] ÷ 6 और (-36) ÷ [(-4) ÷ 6]
∴ [(-36) + (-4)] ÷ 6 = 9 ÷ 6 = 1
और (-36) ÷ [(-4) ÷ 6] = (-36) ÷ -4/6 = 54
अतः [(-36) ÷ (-4)] ÷ 6 (-36) ÷ [(-4) 6]
(iv) [(-100) ÷ (-5)] ÷ 5 और (-100) ÷ [(-5) ÷ 5]
∴ [(-100) + (-5)] + 5 = 20 + 5 =4
और (-100)’ [(-5) ÷ 5] = (-100) ÷ (-1)= 100
अतः [(-100) ÷ (-5)] ÷ 5(-100) ÷ [(-5) ÷ 5]
(v) [75 ÷ (-15)] ÷ (-5) और 75 ÷ [(-15) ÷ (-5)]
∴ [75 ÷ (-15)] ÷ (-5) = (-5) ÷ (-5)=1
और 75 ÷ [(-15) ÷ (-5)] = 75 ÷ 3 = 15
अतः [75 ÷ (-15)] ÷ (-5) = 75 ÷ [(-15) ÷ (-5)]
अतएव कहा जा सकता है कि पूर्णंकों के लिए भाग साहचर्य नहीं है।
प्रयास कीजिए
प्रश्न 1.
किसी भी पूर्णांक a के लिए
(i) 1 ÷ a=1 है ?
(ii) a ÷ (-1) = -a है ? a के विभिन्न मानों के लिए इनकी जाँच कीजिए।
हल:
(i) माना कि a = -1, 1, 3, 5
a = -1 के लिए,
L.H.S. = 1 ÷ a = 1 ÷ (-1)= -1;
R.H.S. = 1 अर्थात्
L.H.S. ≠ R.H.S.
a = 1 के लिए,
L.H.S. = 1 ÷ a = 1 ÷ 1 = 1: R.H.S. = 1
अर्थात् L.H.S. = R.H.S.
a = 3 के लिए,
L.H.S. = 1 ÷ a= 1 ÷ 3 = 1/3 ; R.H.S. = 1
अर्थात् L.H.S. ≠R.H.S.
a = 5 के लिए,
L.H.S. = 1 ÷ a = 1 ÷ 5 = 1/5; R.H.S. = 1
अर्थात् L.H.S. ≠ R.H.S.
अतएव 1 ÷ a = 1 केवल a = 1 के लिए सत्य है।
(ii) माना कि a = 1, 2, 3 , 5
a = 1 के लिए,
L.H.S. = a ÷ (-1)= 1 ÷ (-1)= – 1; .
R.H.S. = – a = -1
अर्थात् L.H.S. = R.H.S.
a = 2 के लिए,
L.H.S. = a ÷ (-1) = 2 ÷ (-1) = – 2 ;
R.H.S. = -a = -2
अर्थात् L.H.S. = R.H.S.
a = 3 के लिए,
L.H.S. = a ÷ (-1) = 3 ÷ (-1) = -3;
R.H.S. = – a = -3
अर्थात् L.H.S. = R.H.S.
a = 5 के लिए,
L.H.S. = a ÷ (-1) = 5 ÷ (-1) = -5;
R.H.S. = -a = -5
अर्थात् L.H.S. = R.H.S.
अतएव प्रत्येक पूर्णांक के लिए, हम पाते हैं :
a ÷ (-1) = -a