Chapter 1 वास्तविक संख्याएँ Ex 1.2

Chapter 1 वास्तविक संख्याएँ Ex 1.2

प्रश्न 1.
निम्नलिखित संख्याओं को अभाज्य गुणनखण्डों के गुणनफल के रूप में व्यक्त कीजिए-
(i) 140
हल-
140 के अभाज्य गुणनखण्ड
= 2 × 70
= 2 × 2 × 35
= 2 × 2 × 5 × 7
= 2² × 5 × 7

(ii) 156
हल-
156 के अभाज्य गुणनखण्ड
= 2 × 78
= 2 × 2 × 39
= 2 × 2 × 3 × 13
= 2² × 3 × 13

(iii) 3825
हल-
3825 के अभाज्य गुणनखण्ड
= 3 × 1275
= 3 × 3 × 425
= 3 × 3 × 5 × 85
= 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

(iv) 5005
हल-
5005 के अभाज्य गुणनखण्ड
= 5 × 1001
= 5 × 7 × 143
= 5 × 7 × 11 × 13

(v) 7429
हल-
7429 के अभाज्य गुणनखण्ड
= 17 × 437
= 17 × 19 × 23

प्रश्न 2.
पूर्णांकों के निम्नलिखित युग्मों के HCF और LCM ज्ञात कीजिए तथा इसकी जाँच कीजिए कि दो संख्याओं का गुणनफल = HCF × LCM है।
(i) 26 और 91
हल-
26 और 91
26 के अभाज्य गुणनखण्ड = 2 × 13
91 के अभाज्य गुणनखण्ड = 7 × 13
∴ 26 और 91 का LCM = 2 × 7 × 13 = 182
तथा 26 और 91 का HCF = 13
सत्यापन – HCF (26, 91) × LCM (26, 91)
= 13 × 182
= 13 × 2 × 91
= 26 × 91
= दी गई संख्याओं का गुणनफल

(ii) 510 और 92
हल-
510 और 92
510 के अभाज्य गुणनखण्ड
= 2 × 255
= 2 × 3 × 85
= 2 × 3 × 5 × 17 ……(i)
तथा 92 के अभाज्य गुणनखण्ड
= 2 × 46
= 2 × 2 × 23
= 2² × 23 …….(ii)
LCM (510, 92) = 2² × 3 × 5 × 17 × 23 = 23460
तथा HCF (510, 92) = 2
सत्यापन – HCF (510, 92) × LCM (510, 92)
= 2 × 23460
= 2 × 2² × 3 × 5 × 17 × 23
= 2 × 3 × 5 × 17 × 2² × 23
= 510 × 92
= दी गई संख्याओं का गुणनफल

(iii) 336 और 54
हल-
336 और 54 336 के अभाज्य गुणनखण्ड = 2 × 168
= 2 × 2 × 84
= 2 × 2 × 2 × 42
= 2 × 2 × 2 × 2 × 21
= 2 × 2 × 2 × 2 × 3 × 7
= 2⁴ × 3 × 7
54 के अभाज्य गुणनखण्ड = 2 × 27
= 2 × 3 × 9
= 2 × 3 × 3 × 3
= 2 × 3³
∴ HCF (336, 54) = 2 × 3 = 6
LCM = 2⁴ × 3³ × 7 = 3024
सत्यापन – HCF (336, 54) × LCM (336, 54)
= 6 × 3024
= 2 × 3 × 2⁴ × 3³ × 7
= 2⁴ × 3 × 7 × 2 × 3³
= 336 × 54
= दी गई संख्याओं का गुणनफल

प्रश्न 3.
अभाज्य गुणनखण्डन विधि द्वारा निम्नलिखित पूर्णांकों के HCF और LCM ज्ञात कीजिए-
(i) 12, 15 और 21
हल-
(i) 12, 15 और 21
12 के अभाज्य गुणनखण्ड = 2 × 2 × 3
15 के अभाज्य गुणनखण्ड = 3 × 5
21 के अभाज्य गुणनखण्ड = 3 × 7
∴ LCM (12, 15 और 21) = 2² × 3 × 5 × 7 = 420
तथा HCF (12, 15 और 21) = 3

(ii) 17, 23 और 29
हल-
17, 23 और 29
17 के अभाज्य गुणनखण्ड = 1 × 17
23 के अभाज्य गुणनखण्ड = 1 × 23
29 के अभाज्य गुणनखण्ड = 1 × 29
∴ LCM (17, 23 और 29) = 17 × 23 × 29 = 11339
तथा HCF (17, 23 और 29) = 1

(iii) 8, 9 और 25
हल-
8, 9 और 25
8 के अभाज्य गुणनखण्ड = 2 × 2 × 2 = (2)³ × 1
9 के अभाज्य गुणनखण्ड = 3 × 3 = (3)² × 1
25 के अभाज्य गुणनखण्ड = 5 × 5 = (5)² × 1
∴ LCM (8, 9 और 25) = (2)³ × (3)² × (5)²
= 8 × 9 × 25
= 1800
तथा HCF (8, 9 और 25) = 1

प्रश्न 4.
HCF (306, 657) = 9 दिया है। LCM (306, 657) ज्ञात कीजिए।
हल-
प्रश्नानुसार संख्याएँ 306 व 657 हैं।
∴ a = 306, b = 657 और H.C.F = 9 दिया है।
हम जानते हैं कि

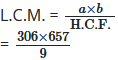
= 34 × 657
= 22338
अतः L.C.M. (306, 657) = 22338

प्रश्न 5.
जाँच कीजिए कि क्या किसी प्राकृत संख्या n के लिए, संख्या 6ⁿ अंक 0 पर समाप्त हो सकती है।
हल-
माना कि किसी प्राकृत संख्या n के लिए, n ∈ N, 6ⁿ अंक 0 पर समाप्त होती है अतः 6ⁿ, 5 से विभाज्य होगी।
परन्तु 6 के अभाज्य गुणनखण्ड 6 = 2 × 3
∴ (6)ⁿ के अभाज्य गुणनखण्ड (6)ⁿ = (2 × 3)ⁿ होंगे।
अर्थात् यह स्पष्ट हो रहा है कि 6ⁿ के अभाज्य गुणनखण्डों में 5 का कोई स्थान नहीं है।
अंकगणित की आधारभूत प्रमेय के आधार पर हम जानते हैं कि प्रत्येक भाज्य संख्या को अभाज्य संख्याओं के गुणनफल के रूप में गुणनखण्डित किया जा सकता है तथा यह गुणनखण्डन अद्वितीय होता है।
अर्थात् हमारी आरम्भ में मानी गई कल्पना असत्य है।
अतः कोई भी प्राकृत संख्या n ऐसी नहीं होगी जिसके लिए 6ⁿ अंक 0 पर समाप्त होती हो।

प्रश्न 6.
व्याख्या कीजिए कि 7 × 11 × 13 + 13 और 17 × 6 × 5 × 4 × 3 × 2 × 1 + 5 भाज्य संख्याएँ क्यों हैं?
हल-
प्रश्नानुसार 7 × 11 × 13 + 13 = 13(7 × 11 + 1)
चूँकि इस प्राप्त संख्या का एक गुणनखण्ड 13 है अतः यह एक भाज्य संख्या है। पुनः प्रश्नानुसार
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = 5 (7 × 6 × 4 × 3 × 2 × 1 + 1)
यह प्राप्त संख्या भी एक भाज्य संख्या है क्योंकि इसका भी एक गुणनखण्ड 5 है।
अतः दी गई दोनों संख्याएँ भाज्य संख्याएँ हैं।

प्रश्न 7.
किसी खेल के मैदान के चारों ओर एक वृत्ताकार पथ है। इस मैदान का एक चक्कर लगाने में सोनिया को 18 मिनट लगते हैं, जबकि इसी मैदान का एक चक्कर लगाने में रवि को 12 मिनट लगते हैं। मान लीजिए वे दोनों एक ही स्थान और एक ही समय पर चलना प्रारम्भ करके एक ही दिशा में चलते हैं। कितने समय बाद वे पुनः प्रारम्भिक स्थान पर मिलेंगे?
हल-
सोनिया द्वारा वृत्ताकार मैदान का 1 चक्कर लगाने का समय = 18 मिनट
रवि द्वारा उसी मैदान का एक चक्कर लगाने में लगा समय = 12 मिनट
यह ज्ञात करने के लिए कि वे पुनः दोनों कितने समय के बाद प्रारम्भिक बिन्दु पर मिलेंगे, हमें 18 व 12 का LCM ज्ञात करना होगा।
अतः 18 के अभाज्य गुणनखण्डन = 2 × 9
= 2 × 3 × 3
= 2 × 3²
तथा 12 के अभाज्य गुणनखण्डन = 2 × 6
= 2 × 2 × 3
= 2² × 3
18 और 12 के सभी अधिकतम घातांक में अभाज्य गुणनखण्डों का गुणनफल लेने पर
∴ LCM (18, 12) = 2² × 3²
= 4 × 9
= 36
अर्थात् सोनिया एवं रवि प्रारम्भिक बिन्दु पर 36 मिनट बाद मिलेंगे।