Chapter 1 Number Systems Ex 1.5

Chapter 1 Number Systems Ex 1.5

Question 1.
Classify the following numbers as rational or irrational.

NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 img 1

Question 2.
Simplify each of the following expressions
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 img 2
Solution:
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 img 3

Question 3.

Question 4.


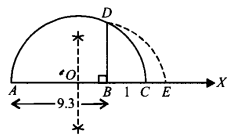
Question 5.
Rationalise the denominator of the following
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 img 5
Solution:
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems Ex 1.5 img 6

{{svg_share_icon}}
0:00
0:00