Chapter 10 वृत्त Ex 10.2
प्रश्न संख्या 1, 2, 3 में सही विकल्प चुनिए एवं उचित कारण दीजिए।
प्रश्न 1.
एक बिन्दु Q से एक वृत्त पर स्पर्श रेखा की लम्बाई 24 cm तथा Q की केन्द्र से दूरी 25 cm है। वृत्त की त्रिज्या है :
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
हल-
एक वृत्त जिसका केन्द्र O है।
बाह्य बिन्दु Q से स्पर्श रेखा PQ की लम्बाई 24 cm तथा Q की केन्द्र O से दूरी 25 cm है।
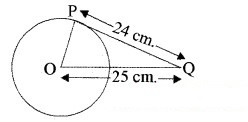
∴ ∠QPO = 90°
अब, समकोण ∆QPQ में,
OQ2 = PQ2 + OP2
या (25)2 = (24)2 + OP2
या 625 = 576 + OP2
या OP2 = 625 – 576
या OP2 = 49 = (7)2
या OP = 7 cm
∴ विकल्प (A) सही है।
प्रश्न 2.
आकृति में, यदि TP, TQ केन्द्र O वाले किसी वृत्त पर दो स्पर्श रेखाएँ इस प्रकार हैं कि ∠POQ = 110°, तो ∠PTQ बराबर है :
(A) 60°
(B) 70°
(C) 80°
(D) 90°
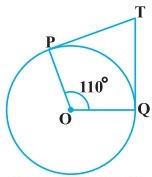
हल-
आकृति में OP त्रिज्या है और PT वृत्त पर स्पर्श रेखा है।
∴ ∠OPT = 90°
इसी प्रकार ∠OQT = 90° और ∠POQ = 110° (दिया है)
अब POQT एक चतुर्भुज है,
∴ ∠POQ + ∠OQT + ∠QTP + ∠TPO = 360°
या 110° + 90° + ∠QTP + 90° = 360°
या ∠QTP + 290° = 360°
या ∠QTP = 360° – 290°
या ∠QTP = 70°
∴ विकल्प (B) सही है।
प्रश्न 3.
यदि एक बिन्दु P से O केन्द्र वाले किसी वृत्त पर PA, PB स्पर्श रेखाएँ परस्पर 80° के कोण पर झुकी हों, तो ∠POA बराबर है :
(A) 50°
(B) 60°
(C) 70°
(D) 80°
हल-
आकृति में OA त्रिज्या है और AP वृत्त पर स्पर्श रेखा है।
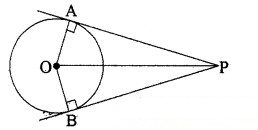
∴ ∠OAP = 90°
इसी प्रकार, ∠OBP = 90°
अब समकोण ∆PAO और ∆PBO में,
∠PAO = ∠PBO = 90°
OP = OP (उभयनिष्ठ भुजा)
OA = OB (एक ही कृत की त्रिज्याएँ)
∴ ∆PAO ≅ ∆PBO [RHS सर्वांगसमता]
∠AOP = ∠BOP
या ∠AOP = ∠BOP = 1/2 ∠AOB …..(i)
साथ ही, चतुर्भुज OAPB में,
∠OBP + ∠BPA + ∠PAO + ∠AOB = 360°
या 90° + 80° + 90° + ∠AOB = 360°
या ∠AOB = 360° – 260°
या ∠AOB = 100° …….(ii)
(i) और (ii) से,
∠AOP = ∠BOP
= 1/2 × 100°
= 50°
∴ विकल्प (A) सही है।
प्रश्न 4.
सिद्ध कीजिए किसी वृत्त के किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ समान्तर होती हैं।
हल-
दिया है : एक वृत्त, जिसका केन्द्र O तथा व्यास AB है।
l और m बिन्दु A और B पर स्पर्श रेखाएँ हैं।
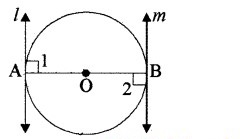
सिद्ध करना है : l || m
उपपत्ति : OA त्रिज्या है और l वृत्त पर स्पर्श रेखा है।
∴ ∠1 = 90°
इसी प्रकार, ∠2 = 90°
अब, ∠1 = ∠2 = 90°
परन्तु यह दो समान्तर रेखाओं के एकान्तर कोण हैं, जब एक तिर्यक रेखा उन्हें काटती है।
∴ l || m
अतः, किसी व्यास के सिरों पर खींची गई स्पर्श रेखाएँ परस्पर समान्तर होती हैं। (इतिसिद्धम्)
प्रश्न 5.
सिद्ध कीजिए कि स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
हल-
दिया है : एक वृत्त जिसका केन्द्र O है।
PQ इसकी स्पर्श रेखा है जो वृत्त को A पर मिलती है।
अर्थात् बिन्दु A वृत्त का स्पर्श बिन्दु है।
सिद्ध करना है : स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है।
रचना : OA को मिलाइए।
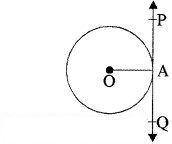
उपपत्ति : क्योंकि OA वृत्त की त्रिज्या है और PQ वृत्त पर स्पर्श रेखा है, जिसमें बिन्दु A स्पर्श बिन्दु है।
∴ ∠OAP = ∠OAQ = 90°
[∵ वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या पर लम्ब होती है।]
या OA ⊥ PQ
क्योंकि किसी वृत्त की त्रिज्या सदैव वृत्त के केन्द्र से गुजरती है।
अतः, स्पर्श बिन्दु से स्पर्श रेखा पर खींचा गया लम्ब वृत्त के केन्द्र से होकर जाता है। (इतिसिद्धम्)
प्रश्न 6.
एक बिन्दु A से, जो एक वृत्त के केन्द्र से 5 cm दूरी पर है, वृत्त पर स्पर्श रेखा की लम्बाई 4 cm है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल-
एक वृत्त जिसका केन्द्र ‘O’ है। वृत्त के बाहर इसके केन्द्र से 5 cm. की दूरी पर कोई बिन्दु A है।
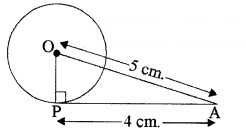
स्पर्श रेखा की लम्बाई = PA = 4 cm
क्योंकि OP त्रिज्या है और PA वृत्त पर स्पर्श रेखा है।
∴ ∠OPA = 90°
अब, समकोण ∆OPA में, पाइथागोरस प्रमेय से,
OA2 = OP2 + PA2
या (5)2 = OP2 + (4)2
या OP2 = 25 – 16
या OP2 = 9 = (3)2
या OP = 3 cm
अतः, वृत्त की त्रिज्या 3 cm है।
प्रश्न 7.
दो संकेन्द्रीय वृत्तों की त्रिज्याएँ 5 cm तथा 3 cm हैं। बड़े वृत्त की उस जीवा की लम्बाई ज्ञात कीजिए जो छोटे वृत्त को स्पर्श करती हो।
हल-
दो संकेन्द्रीय वृत्त जिनका एक ही केन्द्र O तथा त्रिज्याएँ क्रमशः 5 cm और 3 cm हैं।
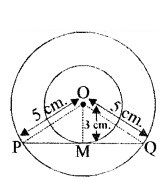
माना कि PQ बड़े वृत्त की जीवा है परन्तु छोटे वृत्त की स्पर्श रेखा है।
क्योंकि, OM छोटे वृत्त की त्रिज्या है और PMQ स्पर्श रेखा है।
∴ ∠OMP = ∠OMQ = 90°
अब, समकोण त्रिभुज OMP और OMQ से,
∠OMP = ∠OMQ = 90°
OP = OQ [एक ही वृत्त की त्रिज्याएँ]
OM = OM [उभयनिष्ठ भुजा]
∴ ∆OMP ≅ ∆OMQ [RHS सर्वांगसमता]
∴ PM = MQ [CPCT]
PQ = 2PM = 2MQ
अब, समकोण ∆OMQ में,
पाइथागोरस प्रमेय से,
OQ2 = OM2 + MQ2
(5)2 = (3)2 + (MQ)2
या MQ2 = 25 – 9
या MQ2 = 16 = (4)2
या MQ = 4 cm
∴ जीवा PQ की लम्बाई = 2MQ
= 2(4) cm
= 8 cm
अतः, अभीष्ट जीवा की लम्बाई 8 cm है।
प्रश्न 8.
एक वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है। (देखिए आकृति)
सिद्ध कीजिए : AB + CD = AD + BC
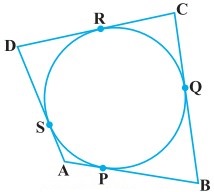
हल-
दिया है : वृत्त के परिगत एक चतुर्भुज ABCD खींचा गया है।
सिद्ध करना है : AB + CD = AD + BC
उपपत्ति: हम जानते हैं कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाई बराबर होती है।
अब, B वृत्त के बाहर स्थित कोई बिन्दु है और BP; BQ वृत्त पर स्पर्श रेखाएँ हैं।
∴ BP = BQ ………(i)
इसी प्रकार, AP = AS …….(ii)
और CR = CQ ……..(iii)
साथ ही, DR = DS …….(iv)
(i), (ii), (iii) और (iv) को जोड़ने पर,
(BP + AP) + (CR + DR) = (BQ + AS) + (CQ + DS)
(BP + AP) + (CR + DR) = (BQ + CQ) + (AS + DS)
AB + CD = BC + DA (इतिसिद्धम्)
प्रश्न 9.
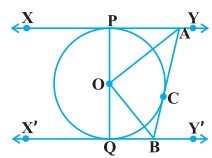
आकृति में, XY तथा X’Y’, O केन्द्र वाले किसी वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं और स्पर्श बिन्दु C पर स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद,करती है। सिद्ध कीजिए कि ∠AOB = 90° है।
हल-
दिया है : XY तथा X’Y’ केन्द्र O वाले वृत्त पर दो समान्तर स्पर्श रेखाएँ हैं
और स्पर्श बिन्दु C पर एक अन्य स्पर्श रेखा AB, XY को A तथा X’Y’ को B पर प्रतिच्छेद करती है।
सिद्ध करना है : ∠AOB = 90°
रचना : OC, OA और OB को मिलाइए।
उपपत्ति : हम जानते हैं कि बाह्य बिन्दु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लम्बाइयाँ समान होती हैं।
अब, A वृत्त के बाहर कोई बिन्दु है जिसमें से दो स्पर्श रेखाएँ PA और AC वृत्त पर खींची गई हैं।
∴ PA = AC
साथ ही, ∆PAO और ∆AOC में,
PA = AC (प्रमाणित)
OA = OA (उभयनिष्ठ भुजा)
OP = OC(एक ही वृत्त की त्रिज्याएँ)
∴ ∆PAO ≅ ∆AOC [SSS सर्वांगसमता]
⇒ ∠PAO = ∠CAO (CPCT]
⇒ ∠PAC = 2∠PAO = 2∠CAO …….(i)
इसी प्रकार ∠QBO = ∠COB
⇒ ∠CBQ = 2∠CBO ………(ii)
अब, ∠PAC + ∠QBC = 90° + 90° = 180°
[∵ OP, OQ त्रिज्याएँ हैं और XY, X’Y’ वृत्त की स्पर्श रेखाएँ हैं।]
या 2∠CAO + 2∠OBC = 180° [(i) और (ii) का प्रयोग करने पर]
![]()
अब, ∆OAB में,
∠CAO + ∠OBC + ∠AOB = 180°
90° + ∠AOB = 180° [(iii) का प्रयोग करने पर]
या ∠AOB = 180° – 90° = 90°
अतः, ∠AOB = 90° (इतिसिद्धम्)
प्रश्न 10.
सिद्ध कीजिए कि किसी बाह्य बिन्दु से किसी |वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण स्पर्श बिन्दुओं को मिलाने वाले रेखाखण्ड द्वारा केन्द्र पर अन्तरित कोण का सम्पूरक होता है।
हल-
दिया है : एक वृत्त जिसका केन्द्र O है।
P वृत्त के बाहर स्थित किसी बिन्दु P से PQ और PR दिए गए वृत्त पर स्पर्श रेखाएँ हैं।
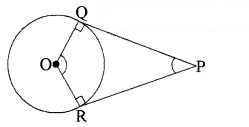
सिद्ध करना है : ∠ROQ + ∠QPR = 180°
उपपत्ति : OQ त्रिज्या है और PQ बिन्दु P से दिए गए वृत्त पर स्पर्श रेखा है।
∴ ∠OQP = 90°
[∵ वृत्त के किसी बिन्दु पर स्पर्श रेखा स्पर्श बिन्द से जाने वाली त्रिज्या पर लम्ब होती है।]
इसी प्रकार, ∠ORP = 90° ……(ii)
अब, चतुर्भुज ROQP में,
∠ROQ + ∠PRO + ∠OQP + ∠QPR = 360°
या ∠ROQ + 90° + 90° + ∠QPR = 360° [समी (i) व (ii) से]
या ∠ROQ + ∠QPR + 180° = 360°
या ∠ROQ + ∠QPR = 360° – 180°
या ∠ROQ + ∠QPR = 180° (इतिसिद्धम्)
प्रश्न 11.
सिद्ध कीजिए कि किसी वृत्त के परिगत समान्तर चतुर्भुज समचतुर्भुज होता है।
हल-
दिया है : एक समान्तर चतुर्भुज ABCD केन्द्र O वाले वृत्त के परिगत है।
सिद्ध करना है : ABCD एक समचतुर्भुज है।
उपपत्ति : हम जानते हैं कि बाह्य बिन्दु से किसी वृत्त पर खींची गई दोनों स्पर्श रेखाओं की लम्बाइयाँ समान होती हैं।
अब, वृत्त के बाहर स्थित किसी बिन्दु B से BE और BF वृत्त पर दो स्पर्श रेखाएँ हैं।
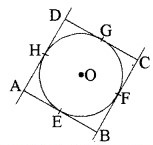
∴ BE = BF ……(1)
इसी प्रकार, AE = AH ……..(2)
और CG = CF ……(3)
साथ ही, DG = DH ……..(4)
(1), (2), (3) और (4) को जोड़ने पर,
(BE + AE) + (CG + DG) = (BF + CF) + (AH + DH)
या AB + CD = BC + AD ……(5)
चूँकि दिया गया है कि ABCD एक समान्तर चतुर्भुज हैं।
∴ AB = CD और BC = AD …….(6)
(5) और (6) से,
AB + AB = BC + BC
या 2AB = 2BC
या AB = BC
इसलिये AB = BC = CD = AD
अतः ABCD एक समचतुर्भुज है। (इतिसिद्धम्)
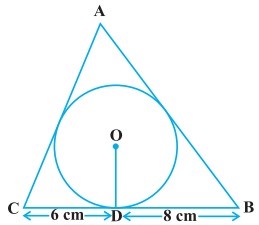
प्रश्न 12.
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज AB इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC (जिनमें स्पर्श बिन्दु D द्वारा BC विभाजित है) की लम्बाइयाँ क्रमशः 8 cm और 6 cm हैं (देखिए आकृति)। भुजाएँ AB और AC ज्ञात कीजिए।
हल-
4 cm त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC खींचा गया है।
त्रिभुज की भुजाएँ BC, CA, AB वृत्त को क्रमशः बिन्दुओं D, E तथा F पर स्पर्श करती हैं।
क्योंकि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
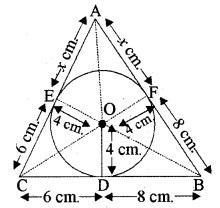
∴ AE = AF = x cm (माना)
∴ CE = CD = 6 cm
और BF = BD = 8 cm
हम जानते हैं कि वृत्त की स्पर्श रेखा स्पर्श बिन्दु से जाने वाली त्रिज्या पर लम्ब होती है।
∴ OD ⊥ AB; OE ⊥ AC और OF ⊥ AB
तथा OE = OD = OF = 4 cm
∆ABC से,
a = CB = (6 + 8) cm = 14 cm
b = AC = (x + 6) cm
c = BA = (8 + x) cm
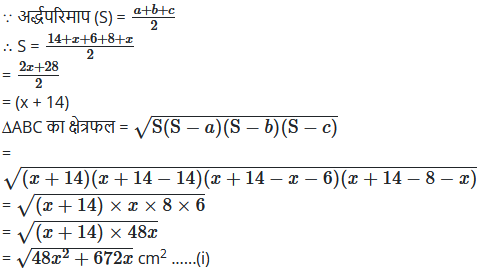

दोनों ओर का वर्ग करने पर
या 48x2 + 672x = 16(x + 14)2
या 48x(x + 14) = 16(x + 14)2
या 3x = x + 14
या 2x = 14
या x = 7
∴ AC = (x + 6) cm = (7 + 6) cm = 13 cm
AB = (x + 8) cm = (7 + 8) cm = 15 cm
अतः, AB = 15 cm और AC = 13 cm
प्रश्न 13.
सिद्ध कीजिए कि वृत्त के परिगत बनी चतुर्भुज की आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण अन्तरित करती हैं।
हल-
दिया है : केन्द्र O वाले वृत्त के परिगत बनी चतुर्भुज PQRS जिसकी भुजाएँ PQ, QR, RS और SP वृत्त को क्रमश: L, M, N, T स्पर्श करती हैं।
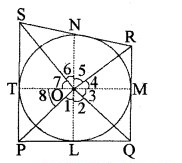
सिद्ध करना है :
∠POQ + ∠SOR = 180°
और ∠SOP + ∠ROQ = 180°
रचना : OP, OL, OQ, OM, OR, ON, OS, OT को मिलाइए।
उपपत्ति : क्योंकि बाह्य बिन्दु से किसी वृत्त पर खींची गई दो स्पर्श रेखाएँ केन्द्र पर समान कोण अन्तरित करती हैं।
∴ ∠2 = ∠3; ∠4 = ∠5; ∠6 = ∠7; ∠8 = ∠1 …..(i)
हम जानते हैं कि एक बिन्दु पर सभी कोणों का जोड़ 360° होता है।
∴ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
या ∠1 + ∠2 + ∠2 + ∠5 + ∠5 + ∠6 + ∠6 + ∠1 = 360°
या 2(∠1 + ∠2 + ∠5 + ∠6) = 360°
![]()
∵ ∠1 + ∠2 = ∠POQ तथा ∠5 + ∠6 = ∠SOR
∴ ∠POQ + ∠SOR = 180°
इसी प्रकार, ∠SOP + ∠ROQ = 180°
अतः वृत्त के परिगत बने चतुर्भुज के आमने-सामने की भुजाएँ केन्द्र पर सम्पूरक कोण आन्तरित करती हैं। (इतिसिद्धम्)