Chapter 10 सरल रेखाएँ Ex 10.2

Chapter 10 सरल रेखाएँ Ex 10.2

प्रश्न 1 से 8 तक रेखा का समीकरण ज्ञात कीजिए जो दिए गए प्रतिबंधों को संतुष्ट करता है।
प्रश्न 1.
x- अक्ष और y- अक्ष के समीकरण लिखिए।
हल:
x- अक्ष का समीकरण y = 0.
तथा y- अक्ष का समीकरण x = 0.

प्रश्न 2.

प्रश्न 3.
बिन्दु (0, 0) से जाने वाली और ढाल m वाली।
हल:
दिया है : बिन्दु (0, 0), ढाल = m
ढाल m, तथा (x₁, y₁) से जाने वाली रेखा का समीकरण
y – y₁ = m(x – x₁)
∴ y – 0 = m(x – 0)
अतः अभीष्ट समीकरण y = mx.

प्रश्न 4.
बिन्दु (2, 2√3) से जाने वाली और x-अक्ष से 75° के कोण पर झुकी हुई।
हल:
चूँकि रेखा x-अक्ष के साथ 75° पर झुकी हुई है, तब रेखा की ढाल
m = tan 75° = tan (45° + 30°)

प्रश्न 5.
मूल बिन्दु के बाईं ओर x- अक्ष को 3 इकाई की दूरी पर प्रतिच्छेद करने तथा ढाल – 2 वाली।
हल:
मूल बिन्दु से बाईं ओर 3 इकाई की दूरी पर स्थित बिन्दु (- 3, 0) होगा तथा ढाल m = – 2
m तथा (x₁, y₁) के द्वारा रेखा का समीकरण,
y – y₁ = m(x – x₁)
वहाँ x₁ = – 3 तथा y₁ = 0 रखने पर,
y – 0 = – 2(x + 3)
या y = – 2x – 6
या 2x + y + 6 = 0.

प्रश्न 6.
मूल बिन्दु से ऊपर y-अक्ष को 2 इकाई की दूरी पर प्रतिच्छेद करने वाली और x-अक्ष की धन दिशा के साथ 30° का कोण बनाने वाली।
हल:
मूल बिन्दु से y-अक्ष पर 2 इकाई की दूरी पर स्थित बिन्दु (0, 2) होगा। x-अक्ष की धन दिशा के साथ रेखा 30° का कोण बनाती है।

प्रश्न 7.
बिन्दुओं (-1, 1) और (2 – 4) से जाते हुए।
हल:

या 3y – 3 = – 5x – 5
अतः 5x + 3y + 2 = 0.

प्रश्न 8.
उस रेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिन्दु से लांबिक दूरी 5 इकाई और लंब धन x-अक्ष से 30° का कोण बनाती है।
हल:
हम जानते हैं कि लंब रूप में रेखा AB का समीकरण,
x cos ω + y sinω = P
यहाँ पर दिया है: ω = 30°, तथा p = 5

∴ रेखा AB का समीकरण,
x cos 30 + y sin 30 = 5

प्रश्न 9.
∆PQR के शीर्ष P(2, 1), Q(- 2, 3) और R(4, 5) हैं। शीर्ष R से जाने वाली माध्यिका का समीकरण ज्ञात कीजिए।
हल:
PQ का मध्य बिन्दु अर्थात् m (0, 2) है।
∴ दो बिन्दुओं से जाने वाली रेखा का समीकरण,

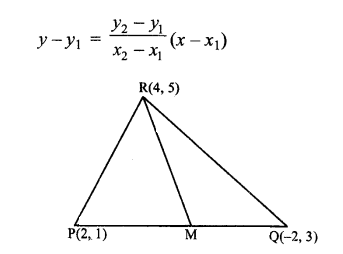
अब बिन्दुओं R (4, 5) तथा M(0, 2) से जाने वाली रेखा का समीकरण,
y – 5 = 2−5/0−4 = (x – 4)
या 4(y – 5) = 3 (x – 4)
या 3x – 4y + 8 = 0
अतः माध्यिका RM का समीकरण 3x – 4y + 8 = 0.

प्रश्न 10.
(- 3, 5) से होकर जाने वाली और बिन्दु (2, 5) और (- 3, 6) से जाने वाली रेखा पर लंब रेखा का समीकरण ज्ञात कीजिए।
हल:
बिन्दु A(2, 5) और B(- 3, 6) से होकर जाने वाली रेखा का ढाल

यदि PL बिन्दु P(- 3, 5) से AB पर लम्ब डाला गया हो तो उसकी ढाल m₂ मान लीजिए।
रेखाएँ PL और AB परस्पर लम्ब हैं।
यदि PL की ढाल × AB की ढाल = – 1

∴ m₂ = 5
PL की ढाल 5 है और P(- 3, 5) से होकर जाती है तो PL का समीकरण,
y – y₁ = m₂(x – x₁)
या y – 5 = 5 (x + 3)
∴ 5x – y + 20 = 0.

प्रश्न 11.
एक रेखा (1, 0) तथा (2, 3) बिन्दुओं को मिलाने वाली रेखाखंड पर लम्ब है तथा उसको 1 : n के अनुपात में विभाजित करती है। रेखा का समीकरण ज्ञात कीजिए।
हल:
रेखा AB बिन्दु A(1, 0) तथा B(2, 3) से होकर जाती है।

PQ रेखा AB को C पर प्रतिछेदन करती है।
साथ ही बिन्दु C रेखाखंड AB को 1 : n के अनुपात में बांटता है।

या (n + 1)x + 3(n + 1)y = n + 2 + 9 = n + 11
या (n+ 1) x + 3 (n + 1)y = n + 11.

प्रश्न 12.
एक रेखा का समीकरण ज्ञात कीजिए जो निर्देशांक अक्षों से समान अंत:खण्ड काटती है और बिन्दु (2, 3) से जाती है।
हल:
(i) रेखा AB बिन्दु P(2, 3) से होकर जाती है और निर्देशांक अक्षों पर समान अंत: खंड बनाती है।
OA = OB
∠BAO = 45°,
∠BAX = 135°

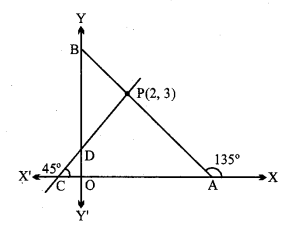
AB की ढाल, m = tan 135° = – 1
रेखा का समीकरण, y – y₁ = m(x – x₁)
जहाँ x₁ = 2, Y₁ = 3 तथा m = – 1
y – 3 = – (x – 2)
या x + y – 5 = 0
या x + y = 5.

प्रश्न 13.
बिन्दु (2, 2) से जाने वाली रेखा का समीकरण ज्ञात कीजिए जिसके द्वारा अक्षों से कटे अंतःखंडों का योग 9 है।
हल:
मान लीजिए P(2, 2) से होकर जाने वाली रेखा से अक्षों पर बने अंतः खंड a तथा b हैं।

अंतः खंड रूप में रेखा का समीकरण

प्रश्न 14.
बिन्दु (0, 2) से जाने वाली और धन x-अक्ष से 2π3 के कोण बनाने वाली रेखा का समीकरण ज्ञात कीजिए। इसके समांतर और y-अक्ष को मूल बिन्दु से 2 इकाई नीचे की दूरी पर प्रतिच्छेद करती हुई रेखा का समीकरण भी ज्ञात करो।
हल:
माना एक रेखा PQ बिन्दु P(0, 2) से होकर जाती है और धन x-अक्ष के साथ 2π3 का कोण बनाती है।
∴ PQ की ढाल = tan2π3
= – 3–√

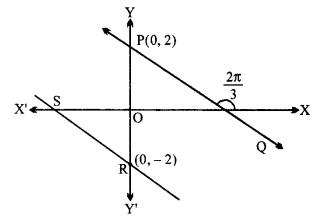
∴ रेखा PQ का समीकरण, y – y₁ = m(x – x₁ )

प्रश्न 15.
मूल बिन्दु से किसी रेखा पर डाला गया लम्ब रेखा से बिन्दु (- 2, 9) पर मिलता है। रेखा का समीकरण ज्ञात कीजिए।
हल:
मान लीजिए रेखा AB पर मूल बिन्दु से डाला गया लम्ब AB पर मिलता है।

परन्तु AB ⊥ OP

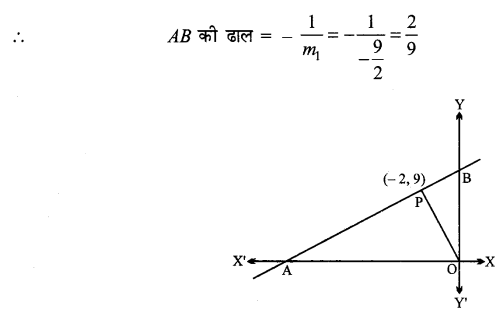
अब AB की ढाल 29 है और P(- 2, 9) से होकर जाती है।
∴ AB का समीकरण
y – y₁ = m(x – x₁)
अर्थात् y – 9 = 2/9 = (x + 2) या
या 9y – 81 = 2x +4
या 2x – 9y + 85 = 0.

प्रश्न 16.
तांबे की छड़ की लम्बाई L (सेमी में) सेल्सियस ताप C का रैखिक फलन है। एक प्रयोग में यदि L= 124.942, जब C = 20 और L= 125.134 जब C = 110 हो, तो L को C के पदों में व्यक्त कीजिए।
हल:
L ताप C का रैखिक फलन है।
(20, 124.942), (110, 125.134) इसका रैखिक फलन है। इन दो बिन्दुओं से संतुष्ट फलन

प्रश्न 17.
किसी दूध भण्डार का स्वामी प्रति सप्ताह 980 लीटर दूध, 14 रू प्रति लीटर के भाव से और 1220 लीटर दूध 16 रू प्रति लीटर के भाव से बेच सकता है। विक्रय मूल्य तथा मांग के मध्य के संबंध को रैखिक मानते हुए ज्ञात कीजिए कि प्रति सप्ताह वह कितना दूध 17 रू प्रति लीटर के भाव से बेच सकता है?
हल:
दूध के भाव और मात्रा में रैखिक सम्बन्ध है। यह रेखा दो बिन्दुओं (14, 980), (16, 1220) से होकर जाती है।
इससे प्राप्त रेखा का समीकरण,

जब x का मान 17 है तो y का मान नीचे दिया गया है।
y = 980 + 120(17 – 14)
= 980 + 120 × 3
= 980 + 360
= 1340
अतः 17 रू प्रति लीटर भाव का 1340 लीटर दूध बिकेगा।

प्रश्न 18.
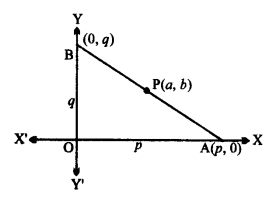
अक्षों के बीच रेखाखंड का मध्य बिंदु P(a, b) है। दिखाइए कि रेखा का समीकरण x/a+y/b = 2 हैं।
P(a, b)
हल:
माना रेखा AB अक्षों पर p और q अंतःखंड बनते हैं।
∴ बिन्दु A और B के क्रमशः निर्देशांक (p, 0) और (0, q) हैं।

प्रश्न 19.
अक्षों के बीच रेखाखण्ड को बिन्दु R(h, k), 1 : 2 के अनुपात में विभक्त करता है। रेखा का समीकरण ज्ञात कीजिए।
हल:
अक्षों के बीच रेखाखंड AB को R(h, k) AR : RB = 1 : 2 के अनुपात में विभक्त करता है।
मान लीजिए अक्षों पर अंत:खण्ड OA = a और OB = b है।

a और b के मान रखने पर,

या 2kx + hy = 3hk.

प्रश्न 20.
रेखा के समीकरण की संकल्पना का प्रयोग करते हुए सिद्ध कीजिए कि तीन बिन्दु (3, 0), (-2,-2) और (8, 2) संरेख हैं।
हल:
बिन्दु A(3, 0), B(- 2, – 2) से होकर जाने वाली रेखा का समीकरण

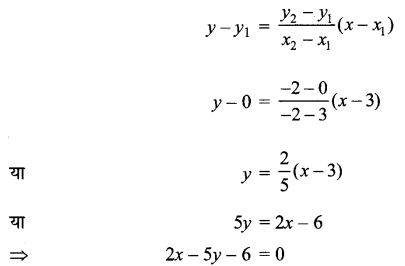
बिन्दु C(8, 2) इस रेखा पर पड़ता है तब इसके निर्देशांक इस समीकरण को संतुष्ट करेंगे।
∴ 2 × 8 – 5 × 2 – 6 = 0
या 16 – 16 = 0
अतः दिए हुए बिन्दु A, B, C सरेख हैं।