Chapter 10 Areas of Parallelograms and Triangles Ex 10.4
Question 1.
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:
Given: parallelogram ABCD and rectangle ABEF are on same base AB, and area of both are equal.
In rectangle ABEF, AB = EF and in parallelogram ABCD,
CD = AB ⇒ AB + CD = AB + EF ….(i)
We know that, the perpendicular distance between two parallel sides of a parallelogram is always less than the length of the other parallel sides.

∴ BE < SC and AF < AD On adding both, we get, BC + AD > BE + AF …(ii)
⇒ BC + AD + AB + CD > BE + AF + AB + CD (Adding AB + CD on both sides)
⇒ AB + BC+ CD + AD > AB + BE + EF + AF [Put the values from Eq. (i)]
Hence, the perimeter of the parallelogram is greater than the perimeter of the rectangle.
Question 2.
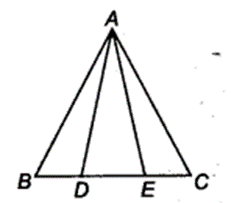
In figure, D and E are two points on BC such that BD = DE = EC. Show that ar(ABD) = ar(ADE) = ar(AEC). Can you now answer the question that you have left in the Introduction’ of this chapter, whether the field of Budhia has been actually divided into three pares of equal area?
[Remark Note that by taking BD = DE = EC, the ∆ ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the sameway, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ∆ ABC into n triangles of equal areas.]
Solution:
Given: ABC is a triangle and D and E are two points on BC, such that

Question 3.
In figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE) = ax(BCF).

Solution:
Given: ABCD, DCFE, and ABFE and parallelograms
In ∆ADE and ∆BCF,
AD = BC (∵ ABCD is a parallelogram)
DE – CF (∵ DCFE is a parallelogram)
and AE = BF (∵ ABFE is a parallelogram)
Hence ∆ADE = ∆BCF
∴ ar (∆ADE) = ar (∆BCF)
Question 4.
In figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(BPC) = ax(DPQ).[Hint Join AC.]

Solution:
Given: ABCD is a parallelogram and AD || CQ, and AQ = CQ. Join the line segment AC.
Now, ∆ APC and ∆ BPC lie on the same base PC and between the same parallels PC and AB, therefore
ar(∆ APC) = ar(∆ BPC) …(i)
AD = CQ and AD || CQ (Given)
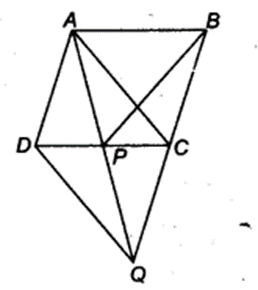
Thus, in quadrilateral ACQD, one pair of opposite sides is equal and parallel.
∴ ADQC is a parallelogram.
We know that, diagonals of a parallelogram bisect each other.
∴ CP = DP and AP = PQ ….(ii)
In ∆ APC and ∆ DPQ, we have

Question 5.
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, Show that

Solution:
Join AD and EC. Let x be the side of ∆ ABC. Then
 src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>
src=”https://farm2.staticflickr.com/1921/31706925298_d4d194aabd_o.png” width=”525″ height=”586″ alt=”NCERT Solutions for Class 9 Maths Chapter 10 Areas of Parallelograms and Triangles 10.4 5b”>


Question 6.
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that
ar(APB) x ar(CPD) = ar(APD) x ar(BPC).
[Hint From A and C, draw perpendiculars to BD.]
Solution:
Given: ABCD is a quadrilateral whose diagonals intersect at P.
Draw two perpendiculars AE and CF from A and Con BD, respectively. Now,
LHS = ar (∆ APB) x ar (∆ CPD)

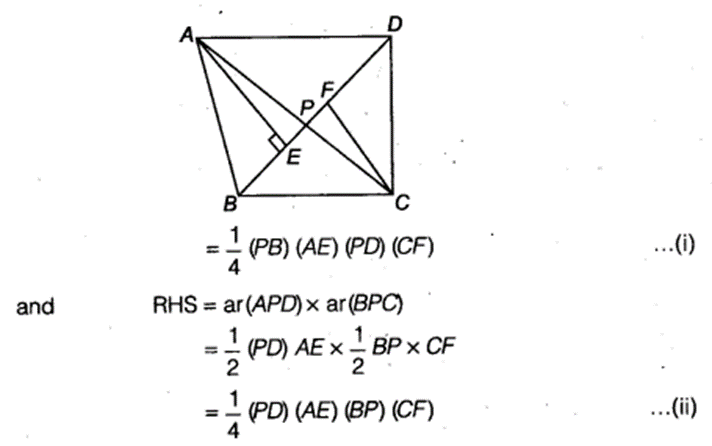
From Eqs. (i) and (ii), we get, LHS = RHS
i.e., ar(∆APB) x ar(∆CPD) = ar(∆APD) x ar(∆BPC)
Question 7.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
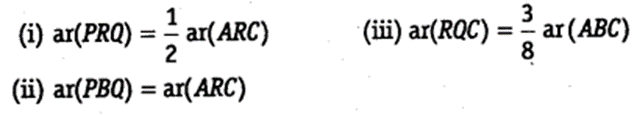
Solution:

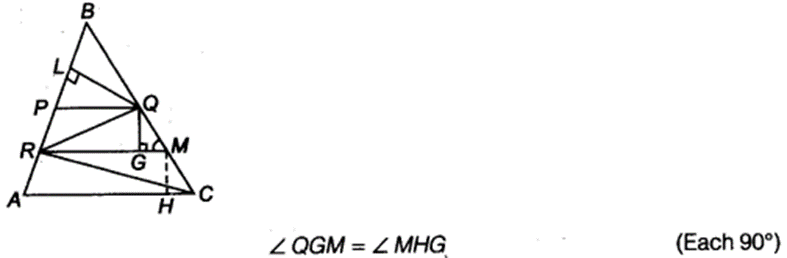


Question 8.
In figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that
(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler, proof of this theorem in Class X.
Solution:
(i) In ∆ABD and ∆MBC,
BC = BD (These are the sides of square)
MB = AB
and ∠ MBC = 90° + ∠ ABC
= ∠DBC + ∠ABC
= ∠ABD
∴ ∆MBC = ∆ABD (By SAS rule)

(iv) In ∆ ACE and ∆FCS,
AC = FC
and CE = BC (These are the sides of square)
∠ FCB = 90° + ∠ ACB = ∠ BCE + ∠ACB = ∠ACE
So, ∆ FCB = ∆ ACE (By SAS rule)
