Chapter 11 क्षेत्रमिति Ex 11.1

Chapter 11 क्षेत्रमिति Ex 11.1

प्रश्न 1.
जैसा कि संलग्न आकृति में दर्शाया गया है, एक आयताकार और एक वर्गाकार खेत के माप दिए हुए हैं। यदि इनके परिमाप समान हैं, तो किस खेत का क्षेत्रफल अधिक होगा?

हल:
माना कि आयताकार खेत की चौड़ाई = b m है।
आयताकार खेत की लम्बाई = 80 m
वर्गकार खेत की भुजा = 60 m
वर्गाकार खेत का परिमाप = 4 x 60 m = 240 m
अब, प्रश्नानुसार, आयत का परिमाप – वर्ग का परिमाप
2(80 + b) = 240
80 + b = = 120
b = (120 – 80) m = 40 m.
अतः आयत की चौड़ाई = 40 m.
अब, वर्गाकार खेत का क्षेत्रफल = (भुजा)² = (60)² m²
= 60 x 60 m² = 3600 m²
आयताकार खेत का क्षेत्रफल = l x b = 80 m x 40 m
= 3200 m²
3600 m² > 3200 m²
अतः वर्गाकार खेत का शेत्रफल अधिक है।

प्रश्न 2.
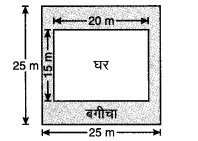
श्रीमती कौशिक के पास चित्र में दर्शाए गए मापों वाला एक वर्गाकार प्लॉट है। वह प्लॉट के बीच में एक घर बनाना चाहती हैं। घर के चारों ओर एक बगीचा विकसित किया गया है। ₹ 55 प्रति वर्ग मीटर की दर से इस बगीचे को विकसित करने का व्यय ज्ञात कीजिए।

हल:
वर्गाकार प्लॉट की भुजा = 25 m
वर्गाकार प्लॉट का क्षेत्रफल= (भुजा) = (25 m)²
= 25 m x 25 m = 625 m²
भीतरी आयत की लम्बाई l = 20 m, चौड़ाई = 15 m
भीतरी आयत का क्षेत्रफल = l x b = 20 m x 15 m
= 300 m²
∴ बगीचे का क्षेत्रफल = वर्गाकार प्लॉट का क्षेत्रफल – भीतरी आयत का क्षेत्रफल
= 625 m² – 300 m²
= 325 m²
₹ 55 प्रति वर्ग मीटर की दर से बगीचे को विकसित करने का व्यय
= ₹ 55 x 325
= ₹ 17,875

प्रश्न 3.
जैसा कि आरेख में दर्शाया गया है, एक बगीचे का आकार मध्य में आयताकार है और किनारों पर अर्धवृत्त के रूप में है। इस बगीचे का परिमाप और क्षेत्रफल ज्ञात कीजिए। (आयत की लम्बाई 20 – (3.5 + 3.5) मीटर है।)

हल:
आयत की लम्बाई = 20 – (3.5 + 3.5) मीटर
= (20 – 7) मीटर = 13 मीटर
आयत की चौड़ाई = 7 मीटर ; वृत्त की त्रिज्या
= मीटर = 3.5 मीटर
बगीचे का परिमाप = 2 x आयताकार भाग की
लम्बाई + दो अर्धवृत्तों का परिमाप
2 x l + 2πr = 2 x 13 + 2 x x 3.5 मीटर
= 26 + 22 मीटर
= 48 मीटर
अतः बगीचे का परिमाप = 48 मीटर
बगीचे का क्षेत्रफल = आयताकार भाग का क्षेत्रफल + 2 अर्धवृत्तों का क्षेत्रफल
= l x b + 2 x πr²
= 13 x 7 + 2 x x x 3.5 x 3.5
= 91 + 38.5 मीटर² = 129.5 मीटर²
अतः बगीचे का क्षेत्रफल = 129.5 मीटर²

प्रश्न 4.
फर्श बनाने के लिए उपयोग की जाने वाली एक टाइल का आकार समान्तर चतुर्भुज का है जिसका आधार 24 cm और संगत ऊँचाई 10 cm है। 1080 वर्ग मीटर क्षेत्रफल के एक फर्श को ढकने के लिए ऐसी कितनी टाइलों की आवश्यकता है? फर्श के कोनों को भरने के लिए आवश्यकतानुसार आप टाइलों को किसी भी रूप में तोड़ सकते हैं।
हल:
समान्तर चतुर्भुज का आधार = 24 सेमी
ऊँचाई = 10 सेमी।
एक टाइल का क्षेत्रफल = आधार x ऊँचाई
= 24 सेमी x 10 सेमी
= 240 सेमी²
फर्श का क्षेत्रफल = 1080 वर्ग मीटर
= 1080 x 100 x 100 वर्ग सेमी

= 45,000 टाइलें
अतः फर्श को ढकने के लिए आवश्यक टाइलों की संख्या = 45,000

प्रश्न 5.
एक चींटी किसी फर्श पर बिखरे हुए विभिन्न आकारों के भोज्य पदार्थ के टुकड़ों के चारों ओर घूम रही है।
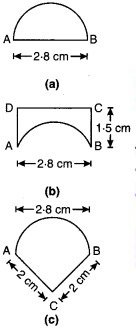
भोज्य पदार्थ के किस टुकड़े के लिए चींटी को लम्बा चक्कर लगाना पड़ेगा? स्मरण रखिए, वृत्त की परिधि c = 2πr, जहाँ r वृत्त की त्रिज्या है, की सहायता से प्राप्त की जा सकती है।

हल:
दी गई आकृतियों पर बिन्दु A, B, C और D अंकित किए। माना कि चींटी प्रत्येक आकृति में भोज्य पदार्थों के टुकड़ों के चारों ओर घूमने के लिए बिन्दु A से प्रारम्भ करके पुनः उसी बिन्दु पर पहुँचती है।

1. भोज्य पदार्थ के (a) टुकड़े के लिए;
यहाँ r = सेमी = 1.4 सेमी
चींटी द्वारा चली गई दूरी= चाप AB + दूरी BA
x 2πr + BA
= x 2 x x 14 + 2.8 सेमी
= 4.4 + 2.8 = 7.2 सेमी

1. भोज्य पदार्थ के (b) टुकड़े के लिए,
चींटी द्वारा चली गई दूरी = चाप AB + दूरी BC + CD + DA
= x 2πr + 1.5 सेमी + 2.8 सेमी + 1.5 सेमी
= x 2 x x 1.4 + 1.5 + 2.8 + 1.5 सेमी
= 4.4 सेमी + 5.8 सेमी
= 10.2 सेमी

3. भोज्य पदार्थ के (c) टुकड़े के लिए,
चींटी द्वारा चली गई दूरी = चाप AB + BC + CA
= x 2πr + 2 सेमी + 2 सेमी
= x 1.4 सेमी + 2 सेमी + 2 सेमी
= 4.4 सेमी + 4 सेमी = 8.4 सेमी
स्पष्ट है कि चींटी को भोज्य पदार्थ (b) टुकड़े के लिए लम्बा चक्कर लगाना पड़ेगा।

पाठ्य-पुस्तक पृष्ठ संख्या # 180

प्रयास कीजिए (क्रमांक 11.2)

प्रश्न 1.
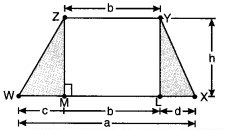
नजमा की बहन के पास भी एक समलम्ब के आकार का प्लॉट है जैसा कि संलग्न आकृति में दर्शाया गया है। इसे तीन भागों में बाँटिए। दर्शाइए कि समलम्ब WXYZ का क्षेत्रफल = h .

हल:
माना कि Y और Z से लम्ब WX पर क्रमशः L तथा M पर मिलते हैं।
तब, समलम्ब WXYZ का क्षेत्रफल
= समकोण ∆LXY का क्षेत्रफल + आयत MLYZ का क्षेत्रफल + समकोण ∆WMZ का क्षेत्रफल
= x LX x YL + ML x LY + x WM x ZM
= x d x h + h x h + + x c x h
= h (d + 2b + c)
= h (2b + c + d)
= h (b + b + c + d)
= h (b + a)
(∴ a = b + c + d)
अतः समलम्ब WXYZ का क्षेत्रफल = h

प्रश्न 2.
यदि h = 10 cm, c = 6 cm, b = 12 cm, d = 4cm, तो इसके प्रत्येक भाग का मान अलग-अलग ज्ञात कीजिए और WXYZ का क्षेत्रफल ज्ञात करने के लिए इनका योग कीजिए। h, a तथा b का मान व्यंजक में रखते हुए इसका सत्यापन कीजिए।
हल:
यहाँ h = 10 cm, c = 6 cm, b = 12 cm, d = 4 cm.
समलम्ब WXYZ का क्षेत्रफल = समकोण ∆LXY का क्षेत्रफल + आयत MLYZ का क्षेत्रफल + समकोण ∆WMZ का क्षेत्रफल
= x d x h + b x h + x c x h
= x 4 x 10 + 12 x 10 + x 6 x 10
= 20 + 120 + 30 = 170 cm²
सत्यापन:
समलम्ब WXYZ का क्षेत्रफल = h
यहाँ, a = c + b + d = 6 cm + 12 cm + 4 cm = 22 cm
∴ समलम्ब का क्षेत्रफल = 10 x cm²
= 5 x 34 cm² = 170 cm²
अतः सूत्र द्वारा क्षेत्रफल का सत्यापन होता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 181

इन्हें कीजिए (क्रमांक 11.1)

प्रश्न 1.
1. आलेख कागज (ग्राफ पेपर) के अन्दर कोई भी समलम्ब WXYZ खींचिए जैसाकि संलग्न आकृति 11.9 में दर्शाया गया है और इसे काटकर बाहर निकालिए।

2. भुजा XY को मोड़कर इसका मध्य बिन्दु ज्ञात कीजिए और इसे A नाम दीजिए (आकृति 11.10)।

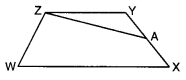
3. भुजा ZA के साथ-साथ काटते हुए समलम्ब WXYZ को दो भागों में काटिए। ∆ZYA को ऐसे रखिए जैसा कि आकृति 11.11 में दर्शाया गया है जिसमें AY को AX के ऊपर रखा गया है। बड़े त्रिभुज के आधार की लम्बाई क्या है? इस त्रिभुज के क्षेत्रफल का व्यंजक लिखिए (आकृति 11.11)।

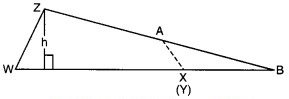
4. इस त्रिभुज और समलम्ब WXYZ का क्षेत्रफल समान है। (कैसे)? त्रिभुज के क्षेत्रफल के व्यंजक का उपयोग करते हुए समलम्ब के क्षेत्रफल का व्यंजक प्राप्त कीजिए।
हल:
3 बड़े त्रिभुज के आधार की लम्बाई
= WB = WX + XB
= WX + ZY
= a+b
∆WBZ का क्षेत्रफल = x आधार x ऊँचाई
= x WB x h
= (a + b) x h
परन्तु समलम्ब WXYZ का क्षेत्रफल = x (a + b) h
∴ समलम्ब का क्षेत्रफल = ∆WBZ का क्षेत्रफल अतः समलम्ब का क्षेत्रफल = x त्रिभुज का आधार x इसकी ऊँचाई

प्रयास कीजिए (क्रमांक 11.3)

प्रश्न 1.
निम्नलिखित समलम्बों का क्षेत्रफल ज्ञात कीजिए (आकृति : 11.12)।

हल:
(i) यहाँ, a = 9 सेमी
b = 7 सेमी तथा
h = 3 सेमी
∴ समलम्ब का क्षेत्रफल = h
∴ समलम्ब का क्षेत्रफल = 3 x वर्ग सेमी
= 3 x वर्ग सेमी
= 24 वर्ग सेमी
अतः समलम्ब का क्षेत्रफल = 24 वर्ग सेमी

(ii) यहाँ, a = 10 सेमी
b = 5 सेमी तथा
h = 6 सेमी
समलम्ब का क्षेत्रफल = h
समलम्ब का क्षेत्रफल = 6 x वर्ग सेमी
= 3 x 15 = 45 वर्ग सेमी
अतः समलम्ब का क्षेत्रफल = 45 वर्ग सेमी

इन्हें कीजिए (क्रमांक 11.2)

प्रश्न 1.
1. कक्षा VII में हमने विभिन्न परिमापों लेकिन समान क्षेत्रफलों वाले समान्तर चतुर्भुजों की रचना करना सीखा है। क्या यह समलम्बों के लिए भी किया जा सकता है? जाँच कीजिए क्या विभिन्न परिमापों वाले निम्नलिखित समलम्ब क्षेत्रफल में समान हैं (आकृति 11.13)

2. हम जानते हैं। कि सभी सर्वांगसम आकृतियाँ क्षेत्रफल में समान होती हैं। क्या हम कह सकते हैं कि समान क्षेत्रफल वाली आकृतियाँ सर्वांगसम भी होती हैं? क्या ये आकृतियाँ सर्वांगसम हैं?
3. एक वर्गाकार शीट पर कम से कम तीन ऐसे समलम्ब खींचिए जिनके परिमाप समान हों परन्तु क्षेत्रफल विभिन्न हों।
हल:
1. हाँ, यह समलम्बों के लिए भी किया जा सकता है।
पहले समलम्ब का क्षेत्रफल = h(a+b)
= x 4 x (10 + 14) वर्ग इकाई

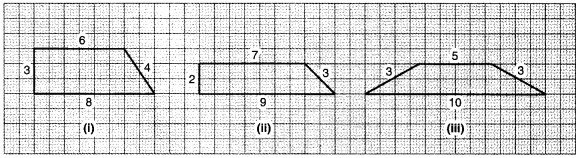
= 2 x 24 वर्ग इकाई
= 48 वर्ग इकाई।
दूसरे समलम्ब का क्षेत्रफल = x (4 + 8) x 8 वर्ग इकाई
= 4 x 12 वर्ग इकाई
= 48 वर्ग इकाई
तीसरे समलम्ब का क्षेत्रफल = x (6 + 10) x 6 वर्ग इकाई
= 3 x 16 वर्ग इकाई
= 48 वर्ग इकाई
पहले समलम्ब का परिमाप = 5 + 10 + 4 + 14 इकाई
= 33 इकाई
दूसरे समलम्ब का परिमाप = 8 + 4 + 8 + 8 इकाई
= 28 इकाई
तीसरे समलम्ब का परिमाप = 6 + 6 + 10 + 7 इकाई
= 29 इकाई
अतः स्पष्ट है कि विभिन्न परिमाप वाले समलम्ब क्षेत्रफल में समान हैं।
2. यह आवश्यक नहीं कि समान क्षेत्रफल वाली आकृतियाँ सर्वांगसम भी हों।
3. ऐसी आकृतियाँ जिनके परिमाप समान हैं परन्तु क्षेत्रफल विभिन्न हैं

पाठ्य-पुस्तक पृष्ठ संख्या # 182

प्रयास कीजिए (क्रमांक 11.4)

प्रश्न 1.
हम जानते हैं कि समान्तर चतुर्भुज भी एक चतुर्भुज है। आइए, इसे भी हम दो त्रिभुजों में विभक्त करते हैं और इन दोनों त्रिभुजों का क्षेत्रफल ज्ञात करते हैं। इस प्रकार समान्तर चतुर्भुज का क्षेत्रफल भी ज्ञात करते हैं। क्या यह सूत्र आपको पूर्व में ज्ञात सूत्र से मेल खाता है (आकृति 11.15)?

हल:
समान्तर चतुर्भुज का क्षेत्रफल = ∆ABC का क्षेत्रफल + ∆BCD का क्षेत्रफल
= x b x h + x b x h
= x (b + b) x h
x 2b x h = b x h = bh
समान्तर चतुर्भुज ABCD का क्षेत्रफल = (समान्तर भुजाओं का योग) – उनके बीच की दूरी
= x (b + b) x h
x 2b x h = bh
हाँ, यह सूत्र पूर्व में ज्ञात सूत्र से मेल खाता है।

पाठ्य-पुस्तक पृष्ठ संख्या # 183

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.1)

प्रश्न 1.
समान्तर चतुर्भुज का विकर्ण खींचकर इसे दो सर्वांगसम त्रिभुजों में बाँटा जाता है। क्या समलम्ब को भी दो सर्वांगसम त्रिभुजों में बाँटा जा सकता है?
उत्तर:
नहीं, समलम्ब को दो सर्वांगसम त्रिभुजों में नहीं बाँटा जा सकता है।

प्रयास कीजिए (क्रमांक 11.5)

प्रश्न 1.
निम्नलिखित चतुर्भुजों का क्षेत्रफल ज्ञात कीजिए (आकृति 11.16)

हल:
(i) यहाँ d = 6 सेमी,
h₁ = 3 सेमी,
h₂ = 5 सेमी

पाठ्य-पुस्तक पृष्ठ संख्या # 184

प्रयास कीजिए (क्रमांक 11.6)

प्रश्न 1.
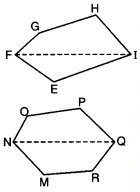
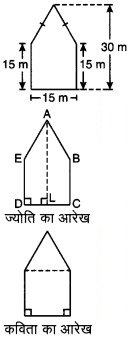
1. निम्नलिखित बहुभुजों (आकृति 11.17) का क्षेत्रफल ज्ञात करने के लिए इन्हें विभिन्न भागों (त्रिभुजों एवं समलम्बो) में विभाजित कीजिए।

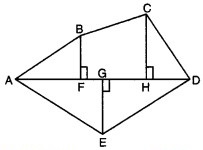
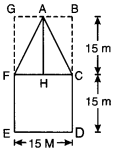
2. बहुभुज ABCDE को विभिन्न भागों में बाँटा गया है जैसा कि आकृति 11.18 में दर्शाया गया है। यदि AD = 8 cm, AH = 6cm, AG = 4cm, AF = 3cm और लम्ब BF = 2cm, CH = 3 cm, EG = 2.5 cm तो इसका क्षेत्रफल ज्ञात कीजिए।
बहुभुज ABCDE का क्षेत्रफल = ∆AFB का क्षेत्रफल + …

3. यदि MP = 9 cm, MD = 7 cm, MC = 6 cm, MB=4cm, MA=2 cm तो बहुभुज MNOPQR(आकृति 11.19) का क्षेत्रफल ज्ञात कीजिए। NA, OC, QD एवं RB विकर्ण MP पर खींचे गए लंब हैं।

हल:
1. दिए गए बहुभुज EFGHI को निम्नांकित भागों में विभाजित किया गया है।
बहुभुज का क्षेत्रफल = ∆FGL का क्षेत्रफल + समलम्ब LGHN का क्षेत्रफल + ∆NHI का क्षेत्रफल + ∆EFI का क्षेत्रफल

= x FL x GL + (GL + HN) x LN + x NI x HN + x FI x ME

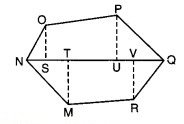
बहुभुज MNOPQR को विभिन्न भागों में विभाजित किया गया है।
बहुभुज MNOPQR का क्षेत्रफल = ∆MTN का क्षेत्रफल + ∆OSN का क्षेत्रफल + समलम्ब OPUS का क्षेत्रफल + ∆PQU का क्षेत्रफल + ∆RVQ का क्षेत्रफल + समलम्ब MTVR का क्षेत्रफल
= x NT x TM + x SN x OS + (OS + PU) x SU + x UQ x PU + x QV x VR + = (TM X VR) x TV

2. यहाँ, AD = 8 सेमी
AH = 6 सेमी
AG = 4 सेमी
AF = 3 सेमी
लम्ब BF = 2 सेमी
CH = 3 सेमी
EG = 2.5 सेमी।
बहुभुज ABCDE का क्षेत्रफल = ∆AFB का क्षेत्रफल + समलम्ब FBCH का क्षेत्रफल + ∆CHD का क्षेत्रफल + ∆ADE का क्षेत्रफल

3. यहाँ, MP= 9 सेमी
MD = 7 सेमी
MC = 6 सेमी
MB = 4 सेमी
MA = 2 सेमी।
बहुभुज MNOPQR का क्षेत्रफल = ∆MNA का क्षेत्रफल + समलम्ब ANOC का क्षेत्रफल + ∆OCP का क्षेत्रफल + AQDP का क्षेत्रफल + समलम्ब BDQR का क्षेत्रफल + ∆RBM का क्षेत्रफल
= AM x MN + x (AN + OC) x AC + CP x OC + DP x DQ + (BN + DQ) – BD + BM x BR
= x 2 x 2.5 वर्ग सेमी + 2x (2.5 + 3) x 4 वर्ग सेमी + x 3 x 3 वर्ग सेमी + x 2 x 2 वर्ग सेमी + x (2.5 + 2) x 3 वर्ग सेमी + x 4 x 2.5 वर्ग सेमी।
= 2.5 + 11.0 + 4.5 + 2 + 6.75 + 500 वर्ग सेमी
= 31.75 वर्ग सेमी।
(∴AC = MC – MA = 6 – 2 = 4 सेमी
CP = MP – MC = 9 – 6 = 3 सेमी
BD = MD – MB = 7 – 4 = 3 सेमी
DP = MP – MD = 9 – 7 = 2 सेमी)