Chapter 11 क्षेत्रमिति Ex 11.2

Chapter 11 क्षेत्रमिति Ex 11.2

प्रश्न 1.
एक मेज के ऊपरी पृष्ठ (सतह) का आकार समलंब जैसा है। यदि इसकी समांतर भुजाएँ 1 m और 1.2 m हैं तथा इन समांतर भुजाओं के बीच की दूरी 0.8 m है, तो इसका क्षेत्रफल ज्ञात कीजिए।

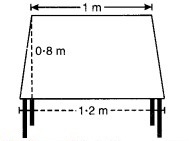
हल:
यहाँ समान्तर भुजाएँ a = 1.2 मी
b = 1 मी
समान्तर भुजाओं के बीच की दूरी h = 0.8 मी
मेज के ऊपरी पृष्ठ का क्षेत्रफल = समलम्ब का क्षेत्रफल
= समान्तर भुजाओं का योग x उनके बीच की दूरी
= (a + b) x h
= (1.2 मी. + 1 मी.) x 0.8 मी
= x 2.2 x 0.8 वर्ग मी.
= 0.88 वर्ग मीटर।
अत: मेज के ऊपरी पृष्ठ का क्षेत्रफल = 0.88 वर्ग मीटर।

प्रश्न 2.
एक समलम्ब का क्षेत्रफल 34 cm² है और इसकी ऊँचाई 4 सेमी है। समान्तर भुजाओं में से एक की 10 cm लम्बाई है। दूसरी समान्तर भुजा की लम्बाई ज्ञात कीजिए।
हल:
समलम्ब का क्षेत्रफल = 34 सेमी²
ऊँचाई = 4 सेमी
समलम्ब की एक समान्तर भुजा = 10 सेमी
माना कि दूसरी समान्तर भुजा = a सेमी
समलम्ब का क्षेत्रफल = x समान्तर भुजाओं का योग x ऊँचाई
34 सेमी² = (10 + a) x 4
10 + a = = 17
a = 17 – 10 = 7 सेमी
अतः समलम्ब की दूसरी समान्तर भुजा की लम्बाई = 7 सेमी।

प्रश्न 3.
एक समलम्ब के आकार के खेत ABCD की बाड़ की लम्बाई 120 m है। यदि BC = 48 m, CD = 17 m और AD = 40 m है, तो इस खेत का क्षेत्रफल ज्ञात कीजिए। भुजा AB समान्तर भुजाओं AD तथा BC पर लंब है।

हल:
खेत ABCD की बाड़ की लम्बाई = 120 मी.
BC = 48 मी
CD = 17 मी और
AD = 40 मी
खेत की बाड़ की लम्बाई = AB + BC + CD + DA
120 मी = AB + 48 मी + 17 मी + 40 मी
120 मी = AB + 105 मी
AB = 120 मी – 105 मी = 15 मी
∴ समलम्ब का क्षेत्रफल = समान्तर भुजाओं का योग x उनके बीच की दूरी।
∴ समलम्ब का क्षेत्रफल = x (48 + 40) x 15 वर्ग मीटर
= x 88 x 15
= 660 वर्ग मीटर।
अतः खेत ABCD का क्षेत्रफल = 660 वर्ग मीटर।

प्रश्न 4.
एक चतुर्भुज आकार के खेत का विकर्ण 24 m है और शेष सम्मुख शीर्षों से इस विकर्ण पर खींचे गए लम्ब 8 m एवं 13 m हैं। खेत का क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ d= 24 मी
h₁ = 13 मी, h₂ = 8 मी

∴ खेत का क्षेत्रफल = x d (h₁ + h₂)
∴ खेत का क्षेत्रफल = x 24 x (13 + 8) मीटर²
x 24 x 21 मीटर² = 252 मीटर²
अतः चतुर्भुज आकार के खेत का क्षेत्रफल = 252 मीटर

प्रश्न 5.
किसी समचतुर्भुज के विकर्ण 7.5 cm एवं 12 cm हैं। इसका क्षेत्रफल ज्ञात कीजिए।
हल:
यहाँ, समचतुर्भुज के विकर्ण = 7.5 सेमी और 12 सेमी हैं।
∴ समचतुर्भुज का क्षेत्रफल= x विकर्णों का गुणनफल
समचतुर्भुज का क्षेत्रफल = x (7.5 x 12) वर्ग सेमी
= 45 वर्ग सेमी।
अतः समचतुर्भुज का क्षेत्रफल = 45 वर्ग सेमी।

प्रश्न 6.
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसकी भुजा 6 cm और शीर्ष लम्ब 4 cm है। यदि एक विकर्ण की लम्बाई 8 cm है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हल:
समचतुर्भुज की भुजा = 6 सेमी
शीर्ष लम्ब = 4 सेमी
एक विकर्ण की लम्बाई =8 सेमी
दूसरे विकर्ण की लम्बाई =d सेमी
समचतुर्भुज का क्षेत्रफल = आधार x शीर्ष लम्ब
= 6 x 4वर्ग सेमी = 24 वर्ग सेमी।
∴ समचतुर्भुज का क्षेत्रफल = x विकर्णों का गुणनफल
∴ 24 वर्ग सेमी = x 8 x d
∴ d = = 6 सेमी
अतः समचतुर्भुज का क्षेत्रफल = 24 वर्ग सेमी
दूसरे विकर्ण की लम्बाई = 6 सेमी।

प्रश्न 7.
किसी भवन के फर्श में समचतुर्भुज के आकार की 3000 टाइलें हैं और इनमें से प्रत्येक के विकर्ण 45 cm और 30 cm लम्बाई के हैं। ₹ 4 प्रति वर्ग मीटर की दर से इस फर्श को पॉलिश करने का व्यय ज्ञात कीजिए।
हल:
टाइल के विकर्ण = 45 सेमी और 30 सेमी
टाइलों की संख्या = 3000
पॉलिश का व्यय = ₹ 4 प्रति वर्ग मीटर
∴ 1 टाइल का क्षेत्रफल = x विकर्णों का गुणनफल
= x 45 x 30 वर्ग सेमी।
= 675 वर्ग सेमी
∴ 3000 टाइलों का क्षेत्रफल = 3000 x 675 वर्ग सेमी
= 2025000 वर्ग सेमी
= वर्ग मीटर
= 202.5 वर्ग मीटर।
∴ फर्श का क्षेत्रफल = 202.5 वर्ग मीटर।
फर्श पर पॉलिश करने का व्यय = ₹ 4 x 202.5
= ₹ 810
अतः फर्श पर पॉलिश करने का व्यय = ₹ 810

प्रश्न 8.
मोहन एक समलम्ब के आकार का खेत खरीदना चाहता है। इस खेत की नदी के साथ वाली भुजा सड़क के साथ वाली भुजा के समान्तर है और लम्बाई में दुगुनी है। यदि इस खेत का क्षेत्रफल 10,500 m हैं और दो समांतर भुजाओं के बीच की लम्बवत् दूरी 100 m है, तो नदी के साथ वाली भुजा की लम्बाई ज्ञात कीजिए।

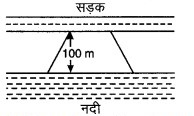
हल:
खेत का क्षेत्रफल = 10,500 m²
माना कि सड़क के साथ वाली भुजा की लम्बाई = x मीटर
नदी के साथ वाली भुजा की लम्बाई = 2x मीटर
दोनों भुजाओं के बीच की दूरी = 100 मीटर
खेत का क्षेत्रफल =
x समान्तर भुजाओं का योग x उनके बीच की दूरी
10500 मी² = x (x + 2x) x 100
3x =
x =
= 70 मीटर
अतः नदी के साथ वाली भुजा की लम्बाई = 2x = 2 x 70
=140 मीटर।

प्रश्न 9.
एक ऊपर उठे हुए चबूतरे का ऊपरी पृष्ठ अष्टभुज के आकार का है जैसा कि आकृति में दर्शाया गया है। अष्टभुजी पृष्ठ का क्षेत्रफल ज्ञात कजिए।

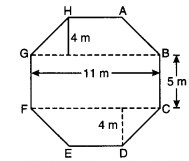
हल:
अष्टभुजी पृष्ठ ABCDEFGH का क्षेत्रफल = समलम्ब ABGH का क्षेत्रफल + आयत BCFG का क्षेत्रफल + समलम्ब CDEF का क्षेत्रफल = x (5 + 11) x 4 + 11 x 5 + x (11 + 5) x 4 वर्ग मीटर
= 32 + 55 + 32 वर्ग मीटर
= 119 वर्ग मीटर।
अतः अष्ठभुजी पृष्ठ का क्षेत्रफल = 119 वर्ग मीटर।

प्रश्न 10.
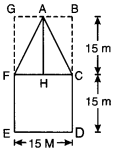
एक पंचभुज आकार का बगीचा है जैसा कि आकृति में दर्शाया गया है। इसका क्षेत्रफल ज्ञात करने के लिए ज्योति और कविता ने इसे दो विभिन्न तरीकों से विभाजित किया। दोनों तरीकों का उपयोग करते हुए इस बगीचे का क्षेत्रफल ज्ञात कीजिए। क्या आप इसका क्षेत्रफल ज्ञात करने की कोई और विधि बता सकते हैं?

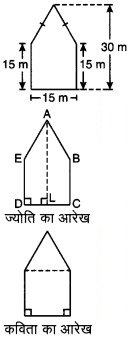
हल:
ज्योति के आरेख द्वारापंचभुज आकार के बगीचे का क्षेत्रफल = 2 x समलम्ब ARCLका क्षेत्रफल
यहाँ, समलम्ब की समान्तर भुजाएँ = 30 मी और 15 मी
समान्तर भुजाओं के बीच की दूरी = मी = 7.5 मी
अतः बगीचे का क्षेत्रफल = 2 x समान्तर भुजाओं का योग x उनके बीच की दूरी
= 2 x (30 + 15) x 7.5 वर्ग मी
= 45 x 7.5 वर्ग मी
= 337.5 वर्ग मीटर।
अत: ज्योति के आरेख द्वारा पंचभुज आकार के बगीचे का क्षेत्रफल = 337.5 वर्ग मीटर।

कविता के आरेख द्वारा:

पंचभुज आकार के बगीचे का क्षेत्रफल = ∆ का क्षेत्रफल + वर्ग का क्षेत्रफल
यहाँ, त्रिभुज का आधार = 15 मीटर
त्रिभुज की ऊँचाई = 15 मीटर
वर्ग की भुजा = 15 मीटर

अतः बगीचे का क्षेत्रफल = x आधार x ऊँचाई + वर्ग की भुजा
= x 15 x 15 + (15)² वर्ग मीटर
= + 225 वर्ग मीटर
= 112.5 + 225 वर्ग मीटर
= 337.5 वर्ग मीटर।
अतः कविता के आरेख द्वारा बगीचे का क्षेत्रफल = 337.5 वर्ग मीटर।

अन्य विधि:

अभीष्ट क्षेत्रफल = आयत BDEG का क्षेत्रफल – 2 x ∆ABC का क्षेत्रफल
= 15 x 30 – 2 x = x 15 वर्गमीटर
= 450 वर्ग मी – 112.5 वर्गमीटर
= 337.5 वर्ग मीटर
अतः बगीचे का अभीष्ट क्षेत्रफल = 337.5 वर्ग मीटर

प्रश्न 11.
संलग्न पिक्चर फ्रेम के आरेख की बाहरी एवं अंतः विमाएँ क्रमशः 24 cm x 28 cm एवं 16 cm x 20 cm हैं। यदि फ्रेम के प्रत्येक खंड की चौड़ाई समान है, तो प्रत्येक – खंड का क्षेत्रफल ज्ञात कीजिए।

हल:

खण्ड ABQP का क्षेत्रफल = खण्ड CDSR का क्षेत्रफल
= x (AB + PQ) x 4 सेमी
= ( 28 + 20) x 4 सेमी²
= 48 x 2 वर्ग सेमी
= 96 वर्ग सेमी।
खण्ड BCRQ का क्षेत्रफल = खण्ड APSD का क्षेत्रफल
= (BC + QR) x 4 वर्ग सेमी
= (24 + 16) x 4 वर्ग सेमी
= 40 x 2 = 80 वर्ग सेमी। उत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 187

ठोस आकार

प्रश्न 1.
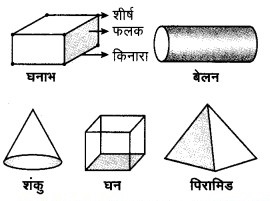
ध्यान दीजिए कि कुछ आकारों में दो या दो से अधिक समरूप (सर्वांगसम) फलक हैं। उनको नाम दीजिए। कौन से ठीसों में सभी फलक सर्वांगसम हैं?

हल:
ठोस आकारों में घनाभ, बेलन, घन और पिरामिड में दो या दो से अधिक फलक समरूप सर्वांगसम हैं। घन में सभी फलक सर्वांगसम हैं।

पाठ्य-पुस्तक पृष्ठ संख्या # 188

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.2)

प्रश्न 1.
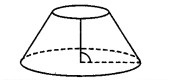
संलग्न आकृति में दर्शाए गए ठोस को बेलन कहना क्यों गलत है?

हल:
बेलन में दो वृत्ताकार सर्वांगसम फलक होते हैं। लेकिन इस आकृति के फलक सर्वांगसम नहीं है।
अतः दिए गए ठोस को बेलन कहना गलत है। उत्तर

पाठ्य-पुस्तक पृष्ठ संख्या # 189

प्रयास कीजिए (क्रमांक 11.7)

प्रश्न 1.
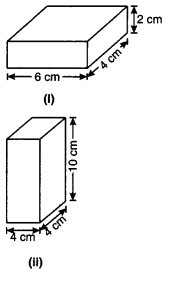
निम्नलिखित घनाभों (आकृति 11.32) का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए –

हल:
(i) लम्बाई l = 6 सेमी
चौड़ाई b = 4 सेमी
ऊँचाई R = 2 सेमी
∵ कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
∵ कुल पृष्ठीय क्षेत्रफल = 2 (6 x 4 + 4 x 2 + 2 x 6) वर्ग सेमी
= 2 (24 + 8 + 12) वर्ग सेमी
= 2 x 44 वर्ग सेमी
= 88 वर्ग सेमी।

(ii) लम्बाई l = 4 सेमी
चौड़ाई b = 4 सेमी
ऊँचाई h = 10 सेमी
∵ कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
∵ कुल पृष्ठीय क्षेत्रफल = 2 (4 x 4 + 4 x 10 + 10 x 4) वर्ग सेमी
= 2 (16 + 40 + 40) वर्ग सेमी
= 2 (96) वर्ग सेमी
= 192 वर्ग सेमी।

पाठ्य-पुस्तक पृष्ठ संख्या # 190

इन्हें कीजिए (क्रमांक 11.3)

प्रश्न 1.
1. एकघनाभाकार डस्टर (जिसे आपके अध्यापक कक्षा में उपयोग करते हैं। के पार्श्व पृष्ठ को भूरे रंग के कागज़ की पट्टी से इस प्रकार ढकिए कि यह डस्टर के पृश्ठ के चारों ओर बिल्कुल ठीक बैठे। कागज़ को हटाइए। कागज़ का क्षेत्रफल मापिए। क्या यह डस्टर का पार्श्व पृष्ठीय क्षेत्रफल है?
2. अपनी कक्षा के कमरे की लम्बाई, चौड़ाई और ऊँचाई मापिए और निम्नलिखित को ज्ञात कीजिए

(a) खिड़कियों और दरवाजों के क्षेत्रफल को छोड़कर कमरे का कुल पृष्ठीय क्षेत्रफल।
(b) इस कमरे का पार्श्व पृष्ठीय क्षेत्रफल।
(c) सफेदी किए जाने वाला, कमरे का कुल क्षेत्रफल।

हल:
1. हाँ, कागज का क्षेत्रफल डस्टर के पार्श्व पृष्ठीय क्षेत्रफल के बराबर है।

2. कक्षा के कमरे की लम्बाई, चौड़ाई तथा ऊँचाई मापने पर,
लम्बाई = 6 मी
चौड़ाई = 5 मी तथा
ऊँचाई = 4 मी

(a) कमरे का कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(6 x 5 + 5 x 4 + 4 x 6) वर्ग मीटर।
= 2 (30 + 20 + 24) वर्ग मीटर
= 2 (74) वर्ग मीटर
= 148 वर्ग मीटर।

(b) कमरे का पार्श्व पृष्ठीय क्षेत्रफल = 2 (l + b)h
= 2 (6 + 5) x 4 वर्ग मीटर
= 2 x 11 x 4 वर्ग मीटर
= 88 वर्ग मीटर।

(c) सफेदी किए जाने वाला कमरे का कुल क्षेत्रफल = कमरे का पार्श्व पृष्ठीय क्षेत्रफल + छत का क्षेत्रफल
= 88 वर्ग मीटर + 6 x 5 वर्ग मीटर
= 88 + 30 वर्ग मीटर
= 118 वर्ग मीटर।

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.3)

प्रश्न 1.
क्या हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 x आधार का क्षेत्रफल।
हल:
हाँ, हम कह सकते हैं कि घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 x आधार का क्षेत्रफल
2 (l + b)h + 2 x lb = 2 (hl + bh + lb)
= 2 (1b + bh + hl)

प्रश्न 2.
यदि हम किसी घनाभ [ आकृति 11.33 (i)] की ऊँचाई और आधार की लम्बाई को परस्पर बदलकर एक दूसरा घनाभ [(आकृति 11.33 (ii)] प्राप्त करलें तो क्या = पार्श्व पृष्ठीय क्षेत्रफल बदल जाएगा?

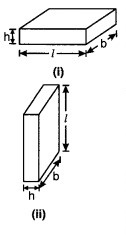
हल:
घनाभ (i) का पार्श्व पृष्ठीय क्षेत्रफल
= 2 (l + b)h ….(1)
तथा घनाभ (ii) का पार्श्व पृष्ठीय क्षेत्रफल
= 2 (h + b)l …(2)
स्पष्ट है कि दोनों पार्श्व पृष्ठीय क्षेत्रफल भिन्न हैं।
अतः ऊँचाई और आधार की लम्बाई को बदलने पर पार्श्व पृष्ठीय क्षेत्रफल बदल जाएगा।

इन्हें कीजिए (क्रमांक 11.4)

प्रश्न 1.
एक वर्गांकित कागज पर दर्शाए गए पैटर्न को खींचिए और उसे काटिए [ आकृति 11.34 (i)]। आप जानते हैं कि यह पैटर्न घन का जाल (नेट) है। इसे रेखाओं के अनुदिश मोडिए[आकृति 11.34 (ii)]और घन बनाने के लिए किनारों पर टेप लगाइए [ आकृति 11.34 (iii) ]।

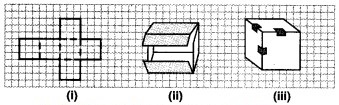
(a) इस घन की लम्बाई, चौड़ाई और ऊँचाई क्या है? ध्यान दीजिए घन के सभी फलक वर्गाकार हैं। = इसलिए घन की लम्बाई, चौड़ाई और ऊँचाई समान होती है (आकृति 11.35)।

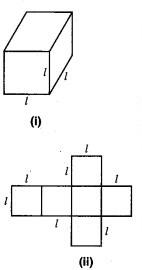
(b) प्रत्येक फलक का क्षेत्रफल लिखिए। क्या सभी फलकों के क्षेत्रफल समान हैं?
(c) इस घन का कुल पृष्ठीय क्षेत्रफल लिखिए।
(d) यदि घन की प्रत्येक भुजा है, तो प्रत्येक फलक का क्षेत्रफल क्या होगा [ आकृति 11:35 (ii)]। क्या हम कह सकते हैं कि । भुजा वाले घन का कुल पृष्ठीय क्षेत्रफल 612 है?
हल:
(a) क्योंकि घन के सभी फलक वर्गाकार आकृति के होते हैं।
अत: घन की लम्बाई = चौड़ाई = ऊँचाई = प्रत्येक 3 इकाई।

(b) प्रत्येक फलक का क्षेत्रफल = (भुजा)²
= (3)² = 9 वर्ग इकाई।
हाँ, सभी फलकों के क्षेत्रफल समान हैं।

(c) घन का कुल पृष्ठीय क्षेत्रफल = 612 वर्ग इकाई
= 6 x (3)²
= 54 वर्ग इकाई।

(d) घन की प्रत्येक भुजा = l
∴ प्रत्येक फलक का क्षेत्रफल = l x l x l²
भुजा वाले घन का पृष्ठीय क्षेत्रफल = 2 (l x l + l x l + l x l)
= 2(l² + l² + l²)
= 2 x 3l² = 6l²
हाँ, हम कह सकते हैं कि ! भुजा वाले घन का कुल पृष्ठीय क्षेत्रफल 612 है।

पाठ्य-पुस्तक पृष्ठ संख्या # 191

प्रयास कीजिए (क्रमांक 11.8)

प्रश्न 1.
घन A का पृष्ठीय क्षेत्रफल और घन B का पार्श्व पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

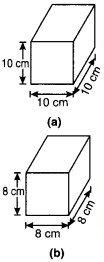
हल:
घन A की लम्बाई = चौड़ाई = ऊँचाई = 10 सेमी घन का पृष्ठीय क्षेत्रफल = 6l²
= 6 x (10)² = 6 x 100
= 600 वर्ग सेमी
अतः घन A का पृष्ठीय क्षेत्रफल = 600 वर्ग सेमी।
घन B की लम्बाई = चौड़ाई = ऊँचाई = 8 सेमी घन B का पार्श्व पृष्ठीय क्षेत्रफल = 2(l + l) x l
= 2 (8 + 8) x 8 वर्ग सेमी
= 2 x 16 x 8 वर्ग सेमी।
= 256 वर्ग सेमी।
अतः घन B का पार्श्व पृष्ठीय क्षेत्रफल = 256 वर्ग सेमी।

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.4)

प्रश्न 1.
1. b भुजा वाले दो घनों को मिलाकर एक घनाभ बनाया गया है (आकृति 11.37) । इस घनाभ का पृष्ठीय क्षेत्रफल क्या है? क्या यह 1252 है? क्या ऐसे तीन घनों को मिलाकर बनाए गए घनाभ का पृष्ठीय क्षेत्रफल 1862 है? क्यों?

2. न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को किस प्रकार व्यवस्थित करेंगे?

3. किसी घन के पृष्ठीय क्षेत्रफल पर पेंट करने के पश्चात् उस घन को समान विमाओं वाले 64 घनों में काटा जाता है (आकृति 11.38)। इनमें से कितने घनों का कोई भी फलक पेंट नहीं हुआ है? कितने घनों का 1 फलक पेंट हुआ है? कितने घनों के 2 फलक पेंट हुए हैं ? कितने घनों के तीन फलक पेंट हुए हैं?

हल:
1. b भुजा वाले दो घनों को मिलाकर बने घनाभ की लम्बाई l = b + b = 2b इकाई, चौड़ाई = b इकाई तथा ऊँचाई = b इकाई इस घनाभ का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (2b x b + b x b + b x 2b)
= 2 (2b² + b² + 2b²)
= 2 x 5b² = 10b² वर्ग इकाई
अत: घनाभ का पृष्ठीय क्षेत्रफल = 10b² वर्ग इकाई उत्तर नहीं, यह 12b² नहीं है।
जब ऐसे तीन घनों को मिलाकर घनाभ बनाया जाता है, तब घनाभ की लम्बाई l = 3b, चौड़ाई = b, ऊँचाई = b इस घनाभ का पृष्ठीय क्षेत्रफल = 2 (3b x b + b x b + b x 3b)
= 2 (3b² + b² + 3b²) वर्ग इकाई
= 2 x 7b² = 14b² वर्ग इकाई
नहीं, इस प्रकार बने घनाभ का पृष्ठीय क्षेत्रफल 18b2 नहीं है। क्योंकि घनाभ की चौड़ाई और ऊँचाई में कोई परिवर्तन नहीं हुआ है।

2. प्रथम स्थिति:
घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को लम्बाई में व्यवस्थित करने पर

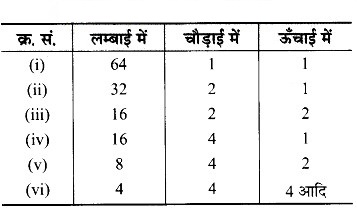
इस स्थिति में, l = 12b
b = b
h = b
पृष्ठीय क्षेत्रफल = 2 (12b x b + b x b + b x 12b)
= 2(12b² + b² + 12b²)
= 2 x 25b² = 50b²

द्वितीय स्थिति:

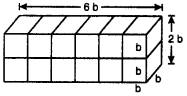
इस स्थिति में,
l = 6b
b = b
h = 2b
∴ इस घनाभ का पृष्ठीय क्षेत्रफल = 2(6b x b + b x 2b + 2b x 6b)
= 2(66² + 2b² + 12b²)
= 2 x 20b² = 40b²

तृतीय स्थिति:

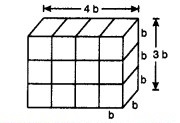
इस स्थिति में,
l = 4b
b = b
h = 3b
∴ इस घनाभ का पृष्ठीय क्षेत्रफल = 2 (4b x b + b x 3b + 3b x 4b)
= 2(4b² + 3b² + 12b²)
= 2 x 19b² = 38b²
अतः न्यूनतम पृष्ठीय क्षेत्रफल का घनाभ निर्मित करने के लिए समान भुजा वाले 12 घनों को तृतीय स्थिति के अनुसार व्यवस्थित करना चाहिए।

3. घनों की संख्या जिनके कोई भी फलक पेंट नहीं हुए = 16
घनों की संख्या जिनका 1 फलक पेंट हुआ = 16
घनों की संख्या जिनके 2 फलक पेंट हुए = 24
घनों की संख्या जिनके 3 फलक पेंट हुए = 8

पाठ्य-पुस्तक पृष्ठ संख्या # 193

प्रयास कीजिए (क्रमांक 11.9)

प्रश्न 1.
निम्नलिखित बेलनों का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए (आकृति : 11.39)

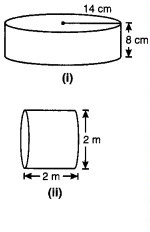
हल:
(i) त्रिज्या r = 14 सेमी
ऊँचाई h = 8 सेमी
बेलन का कुल पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 x 14 (14 + 8)
= 2 x 22 x 2 x 22 वर्ग सेमी
= 1936 वर्ग सेमी
अतः कुल पृष्ठीय क्षेत्रफल = 1936 वर्ग सेमी

(ii) यहाँ, त्रिज्या r = मी = 1 मी
ऊँचाई h = 2 मी
बेलन का पृष्ठीय क्षेत्रफल = 2πr (r + h)
= 2 x x 1 (1 + 2) वर्ग मी
= x 3 वर्ग मी.
= वर्ग मी.
= 186 वर्ग मी.
अत: बेलन का कुल पृष्ठीय क्षेत्रफल = 18 वर्ग मी

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.5)

प्रश्न 1.
नोट कीजिए कि किसी बेलन का पार्श्व पृष्ठीय (वक्र पृष्ठीय क्षेत्रफल) आधार की परिधि x बेलन की ऊँचाई के समान होता है। क्या हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप x घनाभ की ऊँचाई के रूप में लिख सकते हैं?
हल:
माना कि घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः l, b तथा h हैं, तब
घनाभ का पार्श्व पृष्ठीय क्षेत्रफल = 2 (l + b) x h
= आधार का परिमाप x ऊँचाई
अतः हम घनाभ के पार्श्व पृष्ठीय क्षेत्रफल को आधार का परिमाप – घनाभ की ऊँचाई के रूप में लिख सकते हैं।