Chapter 11 क्षेत्रमिति Ex 11.3

Chapter 11 क्षेत्रमिति Ex 11.3

प्रश्न 1.
दो घनाकार डिब्बे हैं जैसा कि संलग्न आकृति में दर्शाया गया है। किस डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता है?

हल:
डिब्बे (a) के लिए –
l = 60 सेमी
b = 40 सेमी
h = 50 सेमी
डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (60 x 40 + 40 x 50 + 50 x 60) वर्ग सेमी
= 2 (2400 + 2000 + 3000) वर्ग सेमी
= 2 (7400) वर्ग सेमी
=14800 वर्ग सेमी

डिब्बे (b) के लिए –
l = 50 सेमी
b = 50 सेमी
h = 50 सेमी
(∴ = b = h = 50 सेमी)
डिब्बे (b) का कुल पृष्ठीय क्षेत्रफल = 6l²
= 6 x (50)² वर्ग सेमी
=6 x 2500 वर्ग सेमी
= 15000 वर्ग सेमी
क्योंकि डिब्बे (a) का कुल पृष्ठीय क्षेत्रफल डिब्बे (b) के कुल पृष्ठीय क्षेत्रफल से कम है।
अतः (a) डिब्बे को बनाने के लिए कम सामग्री की आवश्यकता होगी।

प्रश्न 2.
80 cm x 48 cm x 24 cm माप वाले एक सूटकेस को तिरपाल के कपड़े से ढकना है। ऐसे 100 सूटकेसों को ढकने के लिए 96 cm चौड़ाई वाले कितने मीटर तिरपाल के कपड़े की आवश्यकता है?
हल:
सूटकेस का कुल पृष्ठीय क्षेत्रफल = 2 (80 x 48 + 48 x 24 + 24 x 80) सेमी²
= 2 (3840 + 1152 + 1920) सेमी²
= 2 x 6912 सेमी²
= 13824 सेमी²
100 सूटकेसों का पृष्ठीय क्षेत्रफल =100 x 13824 सेमी² = 100 x मीटर²
माना कि तिरपाल के कपड़े की आवश्यक लम्बाई = x मीटर तिरपाल के कपड़े का वांछित क्षेत्रफल = 100 सूटकेसों का क्षेत्रफल
x × मी² = मी²
(∴ 96 cm = 96100 m)
x = मी
= 144 मीटर
अतः 100 सूटकेसों को ढकने के लिए 144 मीटर तिरपाल के कपड़े की आवश्यकता होगी।

प्रश्न 3.
एक ऐसे घन की भुजा ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 600 cm² है।
हल:
माना कि घन की भुजा = l सेमी है।
घन का पृष्ठीय क्षेत्रफल = 6l²
अब, प्रश्नानुसार,
6l² = 600
l² = = 100
या l = = 10 सेमी
अतः घन की भुजा = 10 सेमी

प्रश्न 4.
रुखसार ने 1 m x 2 m x 1.5 m माप वाली एक पेटी को बाहर से पेंट किया। यदि उसने पेटी के तल के अतिरिक्त उसे सभी जगह से पेंट किया हो तो ज्ञात कीजिए कि उसने कितने पृष्ठीय क्षेत्रफल को पेंट किया।

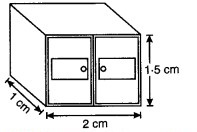
हल:
यहाँ, l = 2 मी
b = 1 मी तथा
h = 1.5 मी
पेंट किया हुआ क्षेत्रफल = lb + 2bh + 21h
= (2 x 1 + 2 x 1 x 1.5 + 2 x 2 x 1.5) मी²
= (2 + 3 + 6) मी²
= 11मी²
अतः रुखसार ने 11 मी² पृष्ठीय क्षेत्रफल को पेंट किया।

प्रश्न 5.
डैनियल एक ऐसे घनाभाकार कमरे की दीवारों और छत को पेंट कर रहा है जिसकी लम्बाई, चौड़ाई और ऊँचाई क्रमशः 15 m, 10 m एवं 7 m हैं। पेंट की प्रत्येक कैन की सहायता से 100 m² क्षेत्रफल को पेंट किया जा सकता है। तो उस कमरे के लिए उसे पेंट की कितनी कैनों की आवश्यकता होगी?
हल:
यहाँ, l = 15 मी
b = 10 मी
h = 7 मी
पेंट किया जाने वाला क्षेत्रफल = lb + 2bh + 2hl
= 15 x 10 + 2 x 10 x 7 + 2 x 7 x 15 मी²
= 150 + 140 + 210 मी²
= 500 मी²

अतः डैनियल को 5 पेंट की कैनों की आवश्यकता होगी।

प्रश्न 6.
वर्णन कीजिए कि दाईं तरफ दी गई आकृतियाँ किस प्रकार एकसमान हैं और किस प्रकार एक दूसरे से भिन्न-भिन्न हैं? किस डिब्बे का पार्श्व पृश्ठीय क्षेत्रफल अधिक है?

हल:
दोनों आकृतियाँ ऊँचाई में एकसमान हैं।
अन्तर:

1. एक आकृति बेलन है और दूसरी आकृति घन है।
2. बेलन के दो वृत्तीय फलक हैं, जबकि घन के छः वर्गाकार फलक हैं।

बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2πrh
यहाँ, l = 5 सेमी = 3.5 सेमी और
h = 7 सेमी
∴ बेलन का पार्श्व पृष्ठीय क्षेत्रफल = 2 x x 3.5 x 7 वर्ग सेमी
= 154 वर्ग सेमी
घन की भुजा = 7 सेमी, ऊँचाई = 7 सेमी
घन का पार्श्व पृश्ठीय क्षेत्रफल = आधार की परिमाप x ऊँचाई
= 4 x 7 x 7 वर्ग सेमी
= 196 वर्ग सेमी
अत: घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है।

प्रश्न 7.
7 m त्रिज्या और 3 m ऊँचाई वाला एक बन्द बेलनाकार टैंक किसी धातु की एक चादर से बना हुआ है। उसे बनाने के लिए वांछित धातु की चादर की मात्रा ज्ञात कीजिए।
हल:
यहाँ, बेलनाकार टैंक की त्रिज्या r = 7 मी और
ऊँचाई h = 3 मी
बन्द बेलनाकार टैंक बनाने के लिए वांछित चादर = बेलन का कुल पृष्ठीय क्षेत्रफल
= 2πr (r + h)
= 2 x x 7x (7 + 3) मी²
= 44 x 10 मी²
= 440 मी²
अत: टैंक बनाने के लिए वांछित धातु की चादर का क्षेत्रफल = 440 मी²

प्रश्न 8.
एक खोखले बेलन का वक्र पृष्ठीय क्षेत्रफल 4224 cm² है। इसे इसकी ऊँचाई के अनुदिश काटकर 32 cm चौड़ाई की एक आयताकार चादर बनाई जाती है। आयताकार चादर का परिमाप ज्ञात कीजिए।
हल:
यहाँ, बेलन का वक्र पृष्ठीय क्षेत्रफल = 4224 cm²
आयताकार चादर की चौड़ाई = 32 cm
खोखले बेलन को काटकर आयताकार चादर बनाई गई है।
∴ बेलन के आधार की परिमाप = आयताकार चादर की लम्बाई तथा बेलन की ऊँचाई = चादर की चौड़ाई
इसलिए, बेलन का वक्र पृष्ठीय क्षेत्रफल = आयताकार चादर का क्षेत्रफल माना कि चादर की लम्बाई = l सेमी है।
∴ आयताकार चादर का क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल
l x 32 = x 4224
l = सेमी = 132 सेमी
अब, आयताकार चादर की परिमाप = 2 (l + b)
= 2 (132 + 32) सेमी
= 2 x 164 सेमी
= 328 सेमी
अत: आयताकार चादर का अभीष्ट परिमाप = 328 सेमी

प्रश्न 9.
किसी सड़क को समतल करने के लिए एक सड़क रोलर को सड़क के ऊपर एक बार घूमने के लिए 750 चक्कर लगाने पड़ते हैं। यदि सड़क रोलर का व्यास 84 cm और लम्बाई 1 m है तो सड़क का क्षेत्रफल ज्ञात कीजिए।

हल:
रोलर बेलनाकार है।
रोलर की त्रिज्या r = सेमी = 42 सेमी = 0.42 मीटर
रोलर की लम्बाई h = 1 मीटर
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x = x 0.42 x 1 मी²
= 2.64 मी²
रोलर द्वारा 750 चक्कर में तय किया क्षेत्रफल = 750 x 2.64 मी² = 1980 मी²
अत: सड़क का क्षेत्रफल = 1980 मी²

प्रश्न 10.
एक कम्पनी अपने दूध पाउडर को ऐसे बेलनाकार बर्तनों में पैक करती है जिनका व्यास 14 cm और ऊँचाई 20 cm है। कम्पनी बर्तन के पृष्ठ के चारों ओर एक लेबल लगाती है (जैसा कि आकृति में दर्शाया गया है)। यदि यह लेबल बर्तन के तल और शीर्ष दोनों से 2 cm की दूरी पर चिपकाया जाता है तो लेबल का क्षेत्रफल क्या है?

हल:
यहाँ, बेलनाकार बर्तन का व्यास = 14 सेमी
∴ बेलनाकार बर्तन की त्रिज्या l = 14 सेमी = 7 सेमी
बेलनाकार बर्तन की ऊँचाई = 20 सेमी
∴ कम्पनी ने बर्तन में लेबल बर्तन के तल और शीर्ष दोनों से 2 सेमी की दूरी पर चिपकाया है। बर्तन पर चिपका हुआ लेबल एक बेलन निर्मित करता है, जिसकी त्रिज्या l = 7 सेमी तथा ऊँचाई = 20 – 4 = 16 सेमी
∴ लेबल का वक्र पृष्ठीय क्षेत्रफल= 2πrh = 2 x x 7 x 16 सेमी²
= 704 सेमी²
अतः लेबल का क्षेत्रफल = 704 सेमी²

पाठ्य-पुस्तक पृष्ठ संख्या # 196

घनाभ

प्रश्न 1.
(i) निम्नलिखित सारणी पर विचार कीजिए और रिक्त स्थानों की पूर्ति कीजिए –
उत्तर:

प्रश्न 1.
(ii) आप क्या देखते करते हैं?
उत्तर:
हम यहाँ यह देखते हैं कि घनाभों को बनाने के लिए 36 घनों का उपयोग किया गया है। इसलिए प्रत्येक घनाभ का आयतन 36 घन इकाई है।
स्पष्ट है कि घनाभ का आयतन = लम्बाई x चौड़ाई x ऊँचाई
अर्थात् घनाभ का आयतन = आधार का क्षेत्रफल x ऊँचाई

पाठ्य-पुस्तक पृष्ठ संख्या # 197

प्रयास कीजिए (क्रमांक 11.10)

प्रश्न 1.
निम्नलिखित घनाभों (आकृति 11.45) का आयतन ज्ञात कीजिए –

हल:
1. यहाँ, 1 = 8 सेमी, b = 3 सेमी तथा h = 2 सेमी
घनाभ का आयतन = l x b x h
= 8 x 3 x 2 = 48 सेमी³

2. यहाँ, आधार का क्षेत्रफल = l x b = 24 सेमी²
ऊँचाई h = 3 सेमी = 100 मी
घनाभ का आयतन = आधार का क्षेत्रफल x ऊँचाई
= 24 मी² x मी = मी³
= 0.72 मी³

घनाभ

प्रयास कीजिए (क्रमांक 11.11)

प्रश्न 1.
निम्नलिखित घनों का आयतन ज्ञात कीजिए –

1. 4 cm भुजा वाला
2. 1.5 m भुजा वाला।

हल:
1. यहाँ, घन की भुजा l = 4 सेमी
∴ घन का आयतन = l³ = (4)³सेमी
= 4 x 4 x 4 सेमी
= 64 सेमी³

2. यहाँ, घन की भुजा l = 1.5 मी
∴ घन का आयतन = = (1.5)³मी
= 1.5 x 1.5 x 1.5 मी³ = 3.375 मी³

इन्हें कीजिए (क्रमांक 11.5)

प्रश्न 1.
समान आकार वाले 64 घनों को जितने रूपों में आप व्यवस्थित कर सकते हैं, उतने रूपों में व्यवस्थित करते हुए घनाभ बनाइए। प्रत्येक रूप का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। क्या समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान होता है?
हल:
कुछ व्यवस्थित रूप इस प्रकार हो सकते हैं। घन इस प्रकार रख सकते हैं –

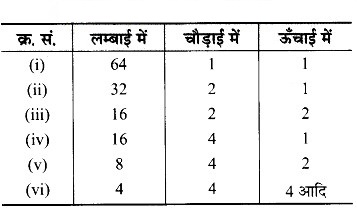
इनके पृष्ठीय क्षेत्रफल क्रमशः इस प्रकार हैं –
∴ पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)

(i) ∴ पृष्ठीय क्षेत्रफल = 2 (64 x 1 + 1 x 1 + 1 x 64)
= 2 x (64 + 1 + 64)
= 2 x 129
= 258 वर्ग इकाई

(ii) पृष्ठीय क्षेत्रफल = 2 (32 x 2 + 2 x 1 + 1 x 32)
= 2 (64 + 2 + 32)
= 2 x 98
= 196 वर्ग इकाई

(iii) पृष्ठीय क्षेत्रफल = 2 (16 x 2 + 2 x 2 + 2 x 16)
= 2(32 + 4 + 32)
= 2 x 68
= 136 वर्ग इकाई

(iv) पृष्ठीय क्षेत्रफल = 2 (16 x 4 +4 x 1 + 1 x 16)
= 2 (64 + 16 + 16)
= 2 x 84
= 168 वर्ग इकाई

(v) पृष्ठीय क्षेत्रफल = 2 (8 x 4 + 4 x 2 + 2 x 8)
= 2 (32 + 8 + 16)
= 2 x 56
= 112 वर्ग इकाई

(vi) पृष्ठीय क्षेत्रफल = 2 (4 x 4 + 4 x 4 + 4 x 4)
= 2 (16 + 16 + 16)
= 2 x 48
= 96 वर्ग इकाई
प्रत्येक स्थिति में आयतन = 64 घन इकाई
यहाँ, स्पष्ट है कि प्रत्येक घन का आयतन तो समान है परन्तु पृष्ठीय क्षेत्रफल भिन्न हैं।
अतः समान आयतन वाली ठोस आकृतियों का पृष्ठीय क्षेत्रफल समान नहीं होता है।

सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 11.6)

प्रश्न 1.
एक कम्पनी बिस्कुट बेचती है। बिस्कुटों को पैक करने के लिए घनाभाकार डिब्बों का उपयोग किया जा रहा है। डिब्बा A → 3 cm x 8 cm x 20 cm, डिब्बा B → 4 cm x 12 cm x 10 cm. डिब्बे का कौन सा आकार कम्पनी के लिए आर्थिक दृष्टि से लाभदायक रहेगा? क्यों? क्या आप ऐसे किसी और आकार (विमाएँ) के डिब्बे का सुझाव दे सकते हैं जिसका आयतन इनके समान हो परन्तु इनकी तुलना में आर्थिक दृष्टि से अधिक लाभदायक हो?
हल:
डिब्बा A:
l = 3 सेमी
b = 8 सेमी
h = 20 सेमी
आयतन = l x b x h = 3 x 8 x 20 सेमी³ = 480 सेमी³
पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 (3 x 8 + 8 x 20 + 20 x 3) सेमी²
= 2 (24 + 160 + 60) सेमी²
= 2 x 244 सेमी²
= 488 सेमी²

डिब्बा B:
l = 4 सेमी
b = 12 सेमी
h = 10 सेमी
आयतन = l x b x h = 4 x 12 x 10 सेमी³ = 480 सेमी³
पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(4 x 12 + 12 x 10 + 10 x 4) सेमी²
= 2 (48 + 120 + 40) सेमी²
= 2 x 208 सेमी²
= 416 सेमी²
यहाँ, डिब्बे A का आयतन = डिब्बे B का आयतन है।
परन्तु डिब्बे A का पृष्ठीय क्षेत्रफल डिब्बे B के पृष्ठीय क्षेत्रफल से अधिक है।
अतः डिब्बा B को बनाने में कम सामग्री की आवश्यकता होगी।
∴ डिब्बे A की अपेक्षा डिब्बा B का आकार कम्पनी के के लिए आर्थिक दृष्टि से अधिक लाभदायक रहेगा।

अन्य डिब्बा:
8 सेमी x 6 सेमी x 10 सेमी
इस डिब्बे का आयतन = 8 x 6 x 10 = 480 सेमी³
इसका पृष्ठीय क्षेत्रफल = 2 (8 x 6+ 6 x 10 + 10 x 8) सेमी²
= 2(48 + 60 + 80) सेमी²
= 2 x 188 सेमी²
= 376 सेमी²
स्पष्ट है कि इस डिब्बे का आयतन डिब्बे B के आयतन के बराबर है। परन्तु इसका पृष्ठीय क्षेत्रफल डिब्बे B के पृष्ठीय क्षेत्रफल से कम है।
अतः दिए हुए डिब्बों की अपेक्षा यह डिब्बा आर्थिक दृष्टि से अधिक लाभदायक है।

पाठ्य-पुस्तक पृष्ठ संख्या # 198

आयतन और धारिता

प्रयास कीजिए (क्रमांक 11.12)

प्रश्न 1.
संलग्न बेलनों का आयतन ज्ञात कीजिए –

हल:
(i) यहाँ, बेलन की त्रिज्या r = 7 सेमी
ऊँचाई h = 10 सेमी
बेलन का आयतन = πr²h
= x 7 x 7 x 10 सेमी³
= 1540 सेमी³

(ii) यहाँ आधार का क्षेत्रफल πr² = 250 मी तथा ऊँचाई = 2 मी
बेलन का आयतन = आधार का क्षेत्रफल x ऊँचाई
= 250 मी² x 2 मी
= 500 मी³