Chapter 11 रचनाएँ Ex 11.1

Chapter 11 रचनाएँ Ex 11.1

निम्न में से प्रत्येक के लिए रचना का औचित्य भी दीजिए:

प्रश्न 1.
7.6 cm लम्बा एक रेखाखण्ड खींचिए और इसे 5 : 8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
हल-
रचना के चरण :

1. सर्वप्रथम रेखाखण्ड AB = 7.6 cm. खींचिए।
2. अब किरण AC खींचिए जो AB के साथ कोई भी न्यून कोण बनाए।
3. किरण AC पर, A से शुरू करके 5 + 8 = 13 बराबर रेखाखण्ड अंकित करें :
AA₁, A₁A₂, A₂A₃, A₃A₄, A₄A₅, A₅A₆, A₆A₇, A₇A₈, A₈A₉, A₉,A₁₀, A₁₀A₁₁, A₁₁A₁₂ और A₁₂A₁₃
4. अब AB को मिलाएँ।
5. A₅ से A₅P || A₁₃B खींचें जो AB से P पर मिले।
6. इस प्रकार, P, AB को 5 : 8 के अनुपात में बाँटता है।
दोनों भागों को मापने पर AP = 2.9 cm और PB = 4.7 cm
स्पष्टीकरण-
∆ABA₁₃ में, PA₅ || BA₁₃
∴ ∆APA₅ ~ ∆ABA₁₃

⇒ AP : PB = 5 : 8

प्रश्न 2.
4 cm, 5 cm और 6 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर इसके समरूप एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 2/3 गुनी हों।
हल-
रचना के चरण : 
1. सर्वप्रथम एक रेखाखण्ड BC = 6 cm खींचिए।
2. अब B को केन्द्र मानकर, 5 cm के बराबर त्रिज्या भरकर एक चाप काटिए।
3. C को केन्द्र मानकर, 4 cm के बराबर त्रिज्या भरकर, पहले वाले चाप को A पर काटते हुए चाप लगाइए।
4. AB और AC को मिलाइए, इस तरह ∆ABC अभीष्ट त्रिभुज होगा।
5. BC के नीचे, एक न्यून कोण CBX बनाइए।
6. BX के साथ, तीन बिन्दु B₁, B₂ और B₃ इस प्रकार अंकित कीजिए कि BB₁ = B₁B₂ = B₂B₃ हो जाएँ।
7. अब B₃C को मिलाइए।
8. B₂ से B₂D || B₃C खींचिए जो BC को D पर मिलता है।
9. D से ED || AC खींचिए जो BA को E पर मिलता है।
इस प्रकार ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 2/3 गुनी होंगी।

स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD

अतः, हमें नया त्रिभुज प्राप्त होता है जो दिए गए त्रिभुज के समान होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 2/3 गुनी के बराबर होती हैं।

प्रश्न 3.
5 cm, 6 cm और 7 cm भुजाओं वाले एक त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 7/5 गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए हुए मान से ∆ABC की रचना कीजिए, जिसमें BC = 7 cm, CA = 6 cm और AB = 5 cm.
2. अब BC के नीचे, न्यून कोण CBX बनाइए।
3. BX के साथ, सात बिन्दु चिह्नित कीजिए : B₁, B₂, B₃, B₄, B₅, B₆, और B₇
इस प्रकार BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇
4. अब B₅C को मिलाइए।
5. B₇ से होकर जाने वाली B₇D || B₅C खींचिए, BC को D तक बढ़ाकर मिलाइए।
6. D से होकर जाने वाली DE || CA खींचिए, जो बढ़ाए गए BA से E पर मिलता है।
इस प्रकार ∆EBD अभीष्ट त्रिभुज होगा, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 7/5 गुनी होंगी।

प्रश्न 4.
आधार 8 cm तथा ऊँचाई 4 cm के एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ इस समद्विबाहु त्रिभुज की संगत भुजाओं की 11/2 गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम BC = 8 cm खींचिए।
2. रेखाखण्ड BC के लम्ब द्विभाजक PQ की रचना कीजिए जो BC पर M से मिले।
3. MP के साथ, MA = 4 cm काटिए।
4. BA और CA को मिलाइए, अब प्राप्त ∆ABC ही अभीष्ट त्रिभुज है।
5. BC को D तक बढ़ाइए, इस तरह कि BD = 12 cm
6. DE || CA खींचिए, BA को आगे बढ़ाकर E पर मिलाइए। 
तब, ∆EBD ही अभीष्ट त्रिभुज होगा।

प्रश्न 5.
एक त्रिभुज ABC बनाइए जिसमें BC = 6 cm, AB = 5 cm और ∠ABC = 60° हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 3/4 गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मानों से ∆ABC की रचना कीजिए जिसमें BC = 6 cm, ∠ABC = 60° और AB = 5 cm.
2. अब BC के नीचे एक न्यून कोण ∠CBX बनाइए।
3. BX के साथ, चार बिन्दु B₁, B₂, B₃, और B₄ लगाइए। इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. फिर B₄C को मिलाइए और B₃D || B₄C खींचिये।
5. अब D से, ED || AC खींचिए जो BA को E पर मिलता है।
फिर ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 3/4 गुनी होंगी।
स्पष्टीकरण-
चूँकि DE || CA
∴ ∆ABC ~ ∆EBD

अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC संगत भुजाओं की 3/4 गुनी होती हैं।

प्रश्न 6.
एक त्रिभुज ABC बनाइए, जिसमें BC = 7 cm, ∠B = 45०, ∠A = 105० हो। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 4/3 गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मान से ∆ABC की रचना कीजिए जिसमें
BC = 7 cm, ∠B = 45°, ∠C = 180° – (∠A + ∠B)
∠C = 180° – (105° + 45°)
= 180° – 150°
= 30°
2. अब BC के नीचे एक न्यून कोण ∠CBX खींचिए।
3. BX के साथ, चार बिन्दु अंकित कीजिए : B₁, B₂, B₃ और B₄ । इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄
4. फिर BC मिलाइए।
5. B₄ से, B₄D || B₃C खींचिए जो बढ़ाए गए BC को D पर मिलता है।
6. D से, ED || AC खींचिए, BA को E तक बढ़ाकर मिलाइए।
फिर ∆EBD अभीष्ट त्रिभुज होगा जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 4/3 गुनी होंगी।
स्पष्टीकरण-
चूँकि, DE || CA
∴ ∆ABC ~ ∆EBD

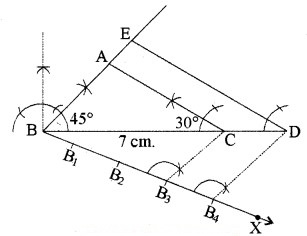
अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 4/3 गुनी होती हैं।

प्रश्न 7.
एक समकोण त्रिभुज की रचना कीजिए, जिसकी भुजाएँ (कर्ण के अतिरिक्त) 4 cm तथा 3 cm लम्बाई की हों। फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए हुए त्रिभुज की संगत भुजाओं की 5/3 गुनी हों।
हल-
रचना के चरण :
1. सर्वप्रथम दिए गए मानों से ∆ABC की रचना कीजिए, जिसमें BC = 4 cm, ∠B = 90° और BA = 3 cm.
2. अब BC के नीचे एक न्यून कोण CBX खींचिए।
3. BX के साथ पाँच बिन्दु अंकित कीजिए : B₁, B₂, B₃, B₄ और B₅ इस तरह BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
4. B₃C को मिलाइए।
5. B₅ से, B₅D || B₃C खींचिए जो बढ़ाए गए BC को D पर मिलता है।
6. D से, ED || AC खींचिए, BA को E तक बढ़ाकर मिलाइए।
तब, ∆EBD अभीष्ट त्रिभुज होगा, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 5/3 गुनी होंगी।
स्पष्टीकरण-
चूँकि, DE || CA
∴ ∆ABC ~ ∆EBD

अतः हमें नया त्रिभुज दिए गए त्रिभुज के समरूप प्राप्त होता है, जिसकी भुजाएँ ∆ABC की संगत भुजाओं की 5/3 गुनी होती हैं।