Chapter 11 Algebra Ex 11.2
Question 1.
The side of an equilateral triangle is shown by l. Express the perimeter of the equilateral triangle using l.
Solution:
Given that the side of an equilateral triangle = l
Perimeter of the equilateral triangle = 3 x side = 3 x l = 3 l units
Question 2.
The side of a regular hexagon (See figure) is denoted by l. Express the perimeter of the hexagon using l.
(Hint: A regular hexagon has all its six sides equal in length)
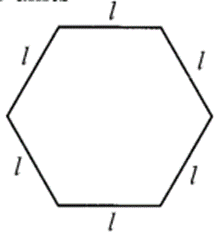
Solution:
Given that each side of a hexagon = l
∴ Perimeter of the regular hexagon = l + l + l + l + l + l
= 6 x l = 6 l units
Question 3.
A cube is a three-dimensional figure as shown in (see figure). It has six faces and all of them are identical squares. The length of an edge of the cube is given by l. Find the formula for the total length of the edges of a cube.
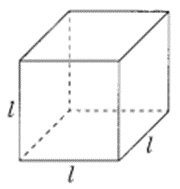
Solution:
We know that a cube has 12 edges and 6 identical faces.
Since all edges are of equal length.
∴ Total length of the edges = 12 x l = 12 l units
∴ Required formula = 12 l units
Question 4.
The diameter of a circle is a line which joins two points on the circle and also passes through the centre of the circle. (In the adjoining figure AB is a diameter of the circle; C is its centre). Express the diameter of the circle (d) in terms of its radius (r).
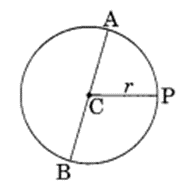
Solution:
Given that radius = r and diameter = d
∴ Diameter = 2 x radius = 2 x r = 2r
So, diameter = 2r.
Question 5.
To find sum of three numbers 14, 27 and 13, we can have two ways;
(a) We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
(b) We may add 27 and 13 to get 13 to get 40 and then add 14 to get the sum 54.
Thus, (14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on whole numbers, in a general way, by using a, b, and c.
Solution:
Given three numbers are a, b and c.
Associative property of addition of numbers = (a + b) + c = a + (b + c)

