Chapter 13 सीधा और प्रतिलोम समानुपात
पाठान्तर्गत प्रश्नोत्तर
पाठ्य-पुस्तक पृष्ठ संख्या # 209
भूमिका
प्रश्न 1.
मोहन स्वयं अपने और अपनी बहन के लिए चाय बनाता है। वह 300 mL पानी, 2 चम्मच चीनी, 1 चम्मच चाय पत्ती और 50 mL दूध का उपयोग करता है। यदि वह पाँच व्यक्तियों के लिए चाय बनाए, तो उसे प्रत्येक वस्तु की कितनी मात्रा की आवश्यकता होगी?
हल:
यहाँ, दो व्यक्तियों के लिए पानी = 300 mL, चीनी = 2 चम्मच, चायपत्ती = 1 चम्मच, दूध = 50 mL.
∴ 2 व्यक्तियों के लिये पानी की मात्रा = 300 mL
∴ 5 व्यक्तियों के लिए पानी की मात्रा = 5 x
= 750 mL
∴ 2 व्यक्तियों के लिए चीनी की मात्रा = 2 चम्मच
∴ 5 व्यक्तियों के लिए चीनी की मात्रा = चम्मच
= 5 चम्मच
∴ 2 व्यक्तियों के लिए चायपत्ती = 1 चम्मच
∴ 5 व्यक्तियों के लिए चायपत्ती = x 5
= 2 चम्मच
∴ 2 व्यक्तियों के लिए दूध की मात्रा = 50 mL
∴ 5 व्यक्तियों के लिए दूध की मात्रा = x 5 mL
= 125 mL
अतः मोहन को 5 व्यक्तियों के लिए चाय बनाने के लिए 750 mL पानी, 5 चम्मच चीनी, 29 चम्मच चायपत्ती और 125 mL दूध की आवश्यकता होगी।
प्रश्न 2.
यदि दो विद्यार्थी किसी सभा के लिए कुर्सियाँ व्यवस्थित करने में 20 मिनट का समय लगाते हैं तो इसी कार्य को करने में 5 विद्यार्थी कितना समय लेंगे?
हल:
∴ 2 विद्यार्थियों को कुर्सियाँ व्यवस्थित करने में लगा समय = 20 मिनट
∴ 5 विद्यार्थियों को कुर्सियाँ व्यवस्थित करने में लगा समय = 2072 मिनट
= 8 मिनट
अत: 5 विद्यार्थियों को कुर्सियाँ व्यवस्थित करने में 8 मिनट लगेंगे।
प्रश्न 3.
ऐसी पाँच और स्थितियाँ लिखिए, जहाँ एक राशि में परिवर्तन होने से दूसरी राशि में परिवर्तन होता है।
उत्तर:
इस प्रकार की पाँच स्थितियाँ निम्नलिखित हैं –
- यदि हम बैंक से अधिक धन उधार लेंगे तो हमें अधिक ब्याज देना होगा।
- किसी गैस पर दबाब बढ़ाने से गैस का आयतन कम हो जाएगा।
- किसी कार्य को करने के लिए मजदूरों की संख्या बढ़ाने पर पहले की अपेक्षा कम दिन लगेंगे।
- अधिक दूरी तय करने के लिए किसी वाहन को अधिक पेट्रोल/डीजल की आवश्यकता होगी।
- किसी मैस में विद्यार्थियों की संख्या बढ़ जाने पर पहले की अपेक्षा अधिक भोजन की आवश्यकता होगी।
पाठ्यपुस्तक पृष्ठ संख्या # 210 सीधा समानुपात
प्रश्न 1.
निम्नलिखित सारणी का अध्ययन कीजिए –
हल:
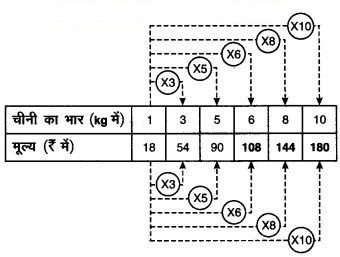
प्रश्न 2.
अब निम्नलिखित सारणी को पूरा कीजिए –
हल: 
पाठ्य-पुस्तक पृष्ठ संख्या # 211-212
इन्हें कीजिए (क्रमांक 13.1)
प्रश्न 1.
एक घड़ी लीजिए और उसकी मिनट वाली (बड़ी) सुई को 12 पर स्थिर कीजिए।
मिनट की सुई द्वारा अपनी प्रारम्भिक स्थिति में घूमे गए कोणों एवं बीते हुए समय को निम्नलिखित सारणी के रूप में लिखिए – 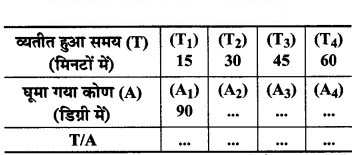
आप T और A के बारे में क्या देखते हैं? क्या इनमें साथ-साथ वृद्धि होती है? क्या – प्रत्येक समय वही रहता है?
क्या मिनट की सुई द्वारा घूमा गया कोण व्यतीत हुए समय के अनुक्रमानुपाती (directly proportional) है? हाँ! उपर्युक्त सारणी से, आप यह भी देख सकते हैं कि –
T1 : T2 = A1 : A2, क्योंकि
T1 : T2 = 15 : 30 = 1 : 2
A1 : A2 = 90 : 180 = 1 : 2
जाँच कीजिए कि क्या T2 : T3 = A2 : A3 तथा T3 : T4 = A3 : A4 है।
आपस्वयं अपने समय अन्तराल लेकर, इस क्रियाकलाप को दोहरा सकते हैं।
हल:
घूमा गया कोण –
A2 → 180°
A3 → 270°
A4 → 360° 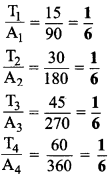
यहाँ, हम देखते हैं कि T में वृद्धि होने पर A में वृद्धि होती है।
हाँ, इनमें साथ-साथ वृद्धि होती है।
हाँ, प्रत्येक समय = रहता है।
“हाँ, मिनट की सुई द्वारा घूमा गया कोण व्यतीत हुए समय के अनुक्रमानुपाती है। 
यहाँ, सत्यापन होता है।
प्रश्न 2.
अपने मित्र से निम्नलिखित सारणी के भरने के लिए कहिए तथा उसकी आयु और उसकी माँ गत आयु का अनुपात ज्ञात करने के लिए भी कहिए – 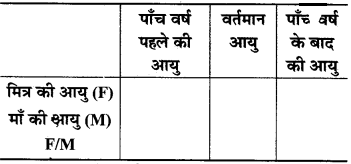
आप क्या देखते हैं? क्या F और M में साथ-साथ वृद्धि (या कमी) होती है? क्या प्रत्येक बार वही रहता है? नहीं। आप इस क्रियाकलाप को अपने अन्य मित्रों के साथ दोहरा सकते हैं तथा अपने प्रेक्षणों को लिख सकते हैं।
हल:
सारणी को भरने पर, 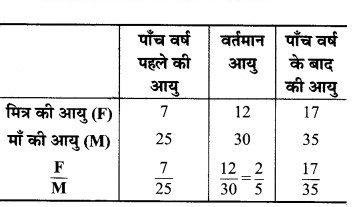
यहाँ, हम देखते हैं कि F और M में साथ-साथ वृद्धि (या कमी) होती है।
नहीं, प्रत्येक बार वही नहीं है।
इस क्रियाकलाप को हम अपने अन्य मित्रों के साथ दोहरा सकते हैं। हम यही स्थिति पाएँगे।
पाठ्य-पुस्तक पृष्ठ संख्या # 212
प्रयास कीजिए (क्रमांक 13.1)
प्रश्न 1.
निम्नलिखित सारणियों को देखिए तथा ज्ञात कीजिए कि क्या x और y अनुक्रमानुपाती हैं –
1. 
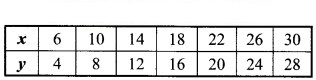
2. 
3. 
हल:
1. ![]()
अतः x और ‘ के संगत मानों का अनुपात , ही रहता है। इसलिए, x और y अनुक्रमानुपाती हैं जिनका अनुपात अचर है।
2.
यहाँ, ![]()
यहाँ x और y का अनुपात अचर नहीं हैं। इसलिए, x और y अनुक्रमानुपाती नहीं हैं।
3. 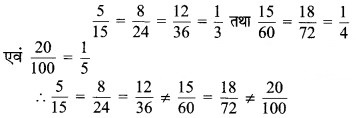
यहाँ, हम देखते हैं कि x और y के संगत अनुपात अचर नहीं हैं।
अतः x और y अनुक्रमानुपाती नहीं हैं। उत्तर
प्रश्न 2.
मूलधन = ₹ 1,000 ब्याज दर = 8% वार्षिक निम्नलिखित सारणी को भरिए तथा ज्ञात कीजिए कि किस प्रकार ब्याज (साधारण या चक्रवृद्धि) समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता या परिवर्तित होता है। 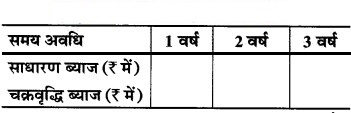
हल:
यहाँ, मूलधन = ₹ 1,000, ब्याज दर = 8% वार्षिक
साधारण ब्याज = 
= ₹ 1259.712 – ₹ 1000
= ₹ 259.712
अब, सारणी भरने पर 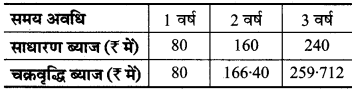
अतः साधारण ब्याज समय अवधि के साथ प्रत्यक्ष अनुपात में बदलता है।
लेकिन चक्रवृद्धि ब्याज समय अवधि के साथ प्रत्यक्ष अनुपात में नहीं बदलता है।
सोचिए, चर्चा कीजिए और लिखिए (क्रमांक 13.1)
प्रश्न 1.
यदि हम समय अवधि और ब्याज की दर स्थिर रखें, तो साधारण ब्याज मूलधन के साथ प्रत्यक्ष अनुपात में परिवर्तित होता है। क्या ऐसा ही सम्बन्ध चक्रवृद्धि ब्याज के लिए भी होगा? क्यों?
हल:
नहीं, ऐसा सम्बन्ध चक्रवृद्धि ब्याज के लिए नहीं होगा। क्योंकि चक्रवृद्धि ब्याज में मूलधन समय अवधि के साथ बदलता रहता है।
पाठ्य-पुस्तक पृष्ठ संख्या # 215
इन्हें कीजिए (क्रमांक 13.2)
प्रश्न 1.
अपने राज्य का एक मानचित्र लीजिए। वहाँ पर प्रयुक्त पैमाने को लिख लीजिए। पैमाने (तनसमत) का प्रयोग करते हुए, मानचित्र पर किन्हीं दो नगरों की दूरी मापिए। इन दोनों नगरों के बीच की वास्तविक दूरी परिकलित कीजिए।
हल:
माना कि पैमाना 1 सेमी. = 200 किमी
माना कि दो नगरों के बीच की दूरी = 4 सेमी
तब, दो नगरों के बीच वास्तविक दूरी = 4 x 200 किमी
= 800 किमी