Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन Ex 13.1
जब तक अन्यथा न कहा जाए, π = 22/7 लीजिए।
प्रश्न 1.
दो घनों, जिनमें से प्रत्येक का आयतन 64 cm3 है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
माना कि घन की प्रत्येक भुजा = x cm
घन का आयतन = 64 cm3
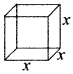
[धन का आयतन = (भुजा)3]
x3 = 64
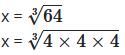
x = 4 cm
∴ घन की भुजा = 4 cm
∵ जब घनों को साथ-साथ जोड़ा जाता है तो घनाभ बन जाता है।
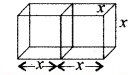
जिसकी लम्बाई = 2x cm = 2 (4) = 8 cm
चौड़ाई = x cm = 4 cm
ऊँचाई = x cm = 4 cm
घनाभ का पृष्ठीय क्षेत्रफल= 2[LB + BH + HL]
= 2[8 × 4 + 4 × 4 + 4 × 8]
= 2[32 + 16 + 32]
= 2[80]
= 160
∴ घनाभ का पृष्ठीय क्षेत्रफल = 160 cm2
प्रश्न 2.
कोई बर्तन एक खोखले अर्द्धगोले के आकार का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्द्धगोले का व्यास 14 cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13 cm है। इस बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
यहाँ अर्द्धगोले का व्यास = बेलन का व्यास = 14 cm
2R = 14 cm
अर्द्धगोले की त्रिज्या (R) = 7 cm
बर्तन की कुल ऊँचाई = 13 cm
∴ बेलन की ऊँचाई = (13 – 7) = 6 cm
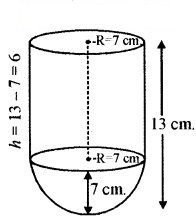
बर्तन का आन्तरिक पृष्ठीय क्षेत्रफल = बेलन का आन्तरिक पृष्ठीय क्षेत्रफल + अर्द्धगोले का आन्तरिक पृष्ठीय क्षेत्रफल
= 2πRH + 2πR2
= 2πR[H + R]
= 2 × 22/7 × 7 (6 + 7)
= 44 × 13
= 572 cm2
अतः बर्तन (पात्र) का कुल आन्तरिक पृष्ठीय क्षेत्रफल का मान = 572 cm2
प्रश्न 3.
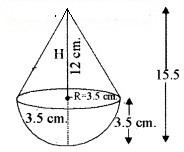
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकार का है, जो उसी त्रिज्या वाले एक अर्द्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 cm है। इस खिलौने का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
यहाँ शंकु की विज्या = अर्द्धगोले की विज्या (R) = 3.5 cm
खिलौने की कुल ऊँचाई = 15.5 cm
∴ शंकु की ऊँचाई. (H) = (15.5 – 3.5) = 12 cm

प्रश्न 4.
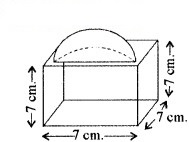
भुजा 7 cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्द्धगोला रखा हुआ है। अर्द्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
प्रश्नानुसार, घनाकार ब्लॉक की भुजा = 7 cm
यहाँ अर्द्धगोले का व्यास = घनाकार ब्लॉक की भुजा = 7 cm
2R = 14

प्रश्न 5.
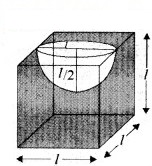
एक घनाकार ब्लॉक के एक फलक को अन्दर की ओर से काट कर एक अर्द्धगोलाकार गड्ढा इस प्रकार बनाया गया है कि अर्द्धगोले का व्यास घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
माना कि घन की भुजा = l
यहाँ अर्द्धगोले का व्यास = घन की भुजा
2R = l
R = l/2
शेष बचे ठोस का पृष्ठीय क्षेत्रफल = घनाभ का कुल पृष्ठीय क्षेत्रफल – घन के तल का क्षेत्रफल + अर्द्धगोले का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
= 6(भुजा)2 – πR2 + 2πR2
= 6(l)2 + πR2
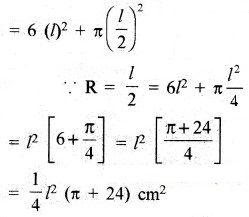
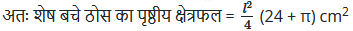
प्रश्न 6.
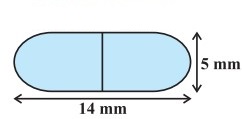
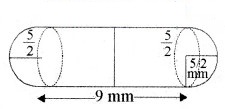
दवा का एक कैप्सूल (capsule) एक बेलन के आकार का है जिसके दोनों सिरों पर एक-एक अर्द्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लम्बाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
यहाँ कैप्सूल का व्यास = अर्द्धगोले का व्यास = बेलन का व्यास = 5 mm
2R = 5 mm
R = 5/2 mm

प्रश्न 7.
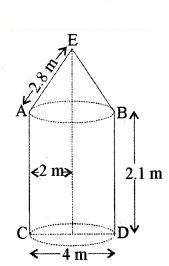
कोई तम्बू एक बेलन के आकार का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 m और 4 m है तथा शंकु की तिर्यक ऊँचाई 2.8 m है तो इस तम्बू को बनाने में प्रयुक्त कैनवास (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500 रु. प्रति m2 की दर से इसमें प्रयुक्त कैनवास की लागत ज्ञात कीजिए।(ध्यान दीजिए कि तम्बू के आधार को कैनवास से नहीं ढका जाता है।)
हल-
यहाँ शंकु का व्यास = बेलन का व्यास
2R = 4
R = 2 m
अतः शंकु की त्रिज्या = बेलन की त्रिज्या = R = 2 m
बेलन की ऊँचाई (H) = 2.1 m
शंकु की तिर्यक ऊँचाई (L) = 2.8 m
तम्बू का वक्र पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + शंक्वाकार भाग का वक्र पृष्ठीय क्षेत्रफल
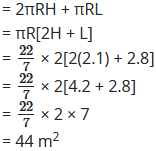
∴ तम्बू का पृष्ठीय क्षेत्रफल = 44 m2
∵ 1 m2 कैनवास की लागत = Rs. 500
∴ 44 m2 कैनवास की लागत = 44 × 500 = 22000 रुपये
प्रश्न 8.
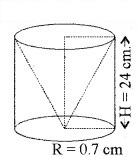
ऊँचाई 2.4 cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेन्टीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल-
बेलन का व्यास (D) = 1.4 cm = शंकु का व्यास
∴ यहाँ बेलन की त्रिज्या = शंकु की त्रिज्या (R) = 0.7 cm
बेलन की ऊँचाई (H) = 2.4 cm
हम जानते हैं कि L2 = R2 + H2
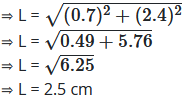
शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + बेलन के ऊपर वाले आधार का क्षेत्रफल + शंकु का पृष्ठीय क्षेत्रफल
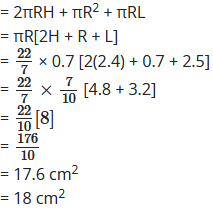
अतः शेष बचे ठोस का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा = 17.6% ~ 18 cm2
प्रश्न 9.
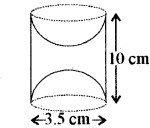
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला खोदकर निकालते हुए, एक वस्तु बनाई गई है, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
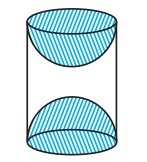
हल-
बेलन की ऊँचाई (H) = 10 cm
यहाँ बेलन की त्रिज्या = अर्द्धगोले की त्रिज्या (R) = 3.5 cm
वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल = बेलन का वक्र पृष्ठीय क्षेत्रफल + 2 अर्द्धगोले का वक्र पृष्ठीय क्षेत्रफल
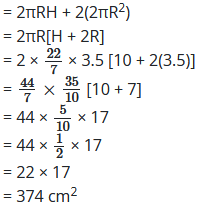
अतः वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल होगा = 374 cm2