Chapter 13 सीमा और अवकलज Ex 13.1
प्रश्न 1 से 22 तक निम्नलिखित सीमाओं के मान प्राप्त कीजिए :
प्रश्न 1.
limx→3 x + 3.
हल:
प्रश्न 2.
![]()
हल:
![]()
प्रश्न 3.
limr→1(πr2).
हल:
![]()
प्रश्न 4.
![]()
हल:

प्रश्न 5.
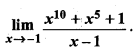
हल:
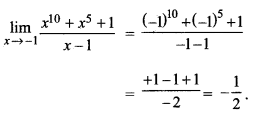
प्रश्न 6.
![]()
हल:

वैकल्पिक विधि : हम जानते हैं :
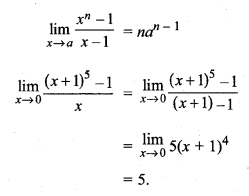
प्रश्न 7.
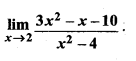
हल:
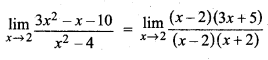
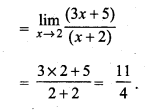
प्रश्न 8.
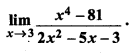
हल:

प्रश्न 9.
![]()
हल:

प्रश्न 10.
![]()
हल:
![]()
प्रश्न 11.
![]()
हल:
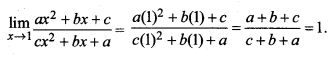
प्रश्न 12.
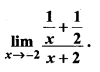
हल:

प्रश्न 13.
![]()
हल:
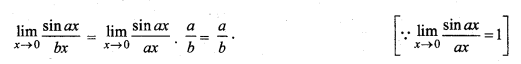
प्रश्न 14.
![]()
हल:
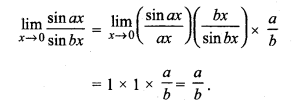
प्रश्न 15.
![]()
हल:

प्रश्न 16.
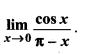
हल:
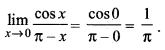
प्रश्न 17.
![]()
हल:
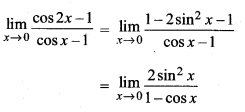
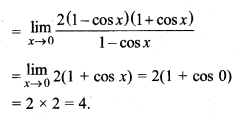
प्रश्न 18.
![]()
हल:

प्रश्न 19.
![]()
हल:
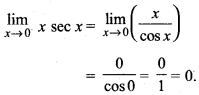
प्रश्न 20.
![]()
हल:

प्रश्न 21.
![]()
हल:
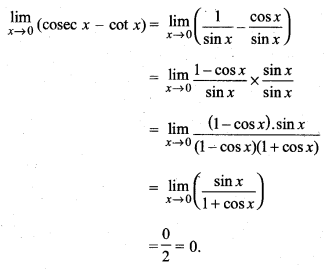
प्रश्न 22.
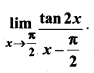
हल:

प्रश्न 23.
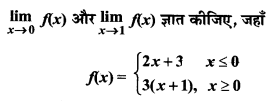
हल:

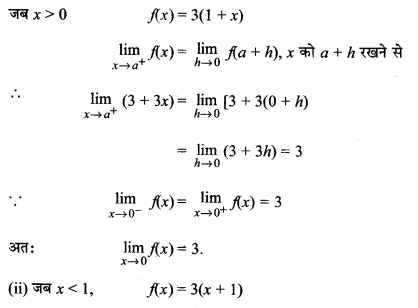

प्रश्न 24.
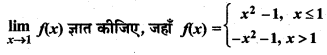
हल:

समी (i) और (ii) से,
![]()
∴ अतः x = 1 पर सीमा का अस्तित्व नहीं है।
प्रश्न 25.

हल:
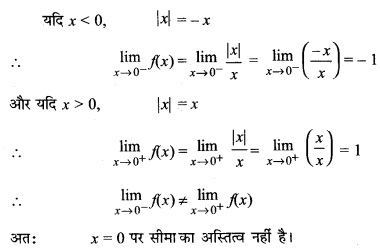
प्रश्न 26.

हल:

प्रश्न 27.
limx→5 f(x) ज्ञात कीजिए, जहाँ f(x) = |x|- 5.
हल:
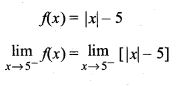
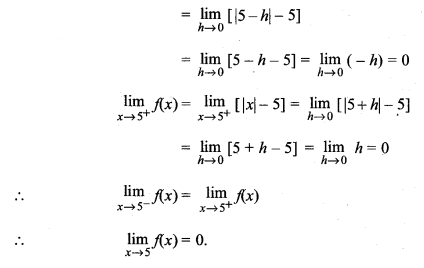
प्रश्न 28.

और यदि limx→1 f(x) = f(1), तो a और b के संभव मान क्या हैं?
हल:

समी (i) और (ii) को जोड़ने पर,
2b = 8 या b = 4
समी (i) में b = 4 रखने पर,
4 + a = 4 या a = 0
अतः a = 0, b = 4.
प्रश्न 29.
मान लीजिए a1,a2,…..an, अचर वास्तविक संख्याएँ हैं और एक फलन f(x) = (x – a1) (x – a2)…..(x – an) से परिभाषित है। limx→a1 f(x) क्या है? किसी a ≠ a1,a2,…..an के लिए limx→a f(x) का परिकलन कीजिए।
हल:

प्रश्न 30.

हल:
दिया गया फलन:
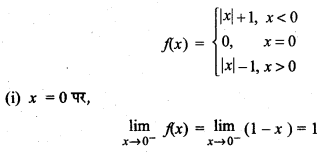

अतः सभी a, a ≠ 0 के लिए limx→a f(x) का अस्तित्व है।
प्रश्न 31.

हल:
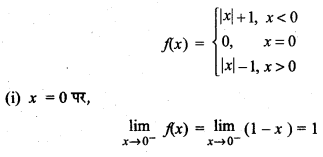

प्रश्न 32.
किन पूर्णांकों m और n के लिए limx→0 f(x) और limx→1 f(x) दोनों का अस्तित्व है, यदि

हल:

अतः limx→0 f(x) के अस्तित्व हेतु m = n अनिवार्य रूप से होना चाहिए; m तथा n के किसी भी पूर्णांक मान के लिए limx→1 f(x) का अस्तित्व है।