Chapter 13 Exponents and Powers Exercise 13.2

Chapter 13 Exponents and Powers Exercise 13.2

Question 1.
Using laws of exponents, simplify and write the answer in exponential form:

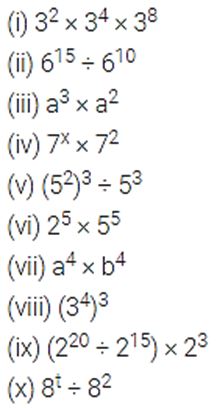
Question 2.
Simplify and express each of the following in exponential form:

Solution:

Question 3.
Say true or false and justify your answer:
(i) 10 × 10¹¹ = 100¹¹
(ii) 2³ > 5²
(iii) 2³ × 3² = 6⁵
(iv) 3²⁰ = (1000)⁰
Solution:
(i) 10 × 10¹¹ = 10¹⁺¹¹ = 10¹²
RHS = 100¹¹ = (10²)¹¹ = 10²²
10¹² ≠ 10²²
∴ Statement is false.

(ii) 2³ > 5²
LHS = 2³ = 8
RHS = 5²2 = 25
8 < 25
∴ 2³ < 5²
Thus, the statement is false.

(iii) 2³ × 3² = 6⁵
LHS = 2³3 × 3² = 8 × 9 = 72
RHS = 6⁵ = 6 × 6 × 6 × 6 × 6 = 7776
∴ 72 ≠ 7776
∴ The statement is false.

(iv) 3⁰ = (1000)⁰
⇒ 1 = 1 True [∵ a⁰ = 1]

Question 4.
Express each of the following as a product of prime factors only in exponential form:
(i) 108 × 192
(ii) 270
(iii) 729 × 64
(iv) 768
Solution:
(i) 108 × 192 = 2 × 2 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
=2⁸ × 3⁴

(iii) 729 × 64 = 3 × 3 × 3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2 × 2
=3⁶ × 2⁶

Question 5.
Simplify:

Solution: