Chapter 16 प्रायिकता विविध प्रश्नावली

Chapter 16 प्रायिकता विविध प्रश्नावली

प्रश्न 1.
एक डिब्बे में 10 लाल, 20 नीली व 30 हरी गोलियाँ रखी हैं। डिब्बे से 5 गोलियाँ यादृच्छया निकाली जाती हैं। प्रायिकता क्या है कि
(i) सभी गोलियाँ नीली हैं?
(ii) कम से कम एक गोली हरी है ?
हल:
एक डिब्बे में 10 लाल, 20 नीली तथा 30 हरी कुल 60 गोलियाँ हैं।
(i) 60 गोलियों में से 5 गोलियाँ निकालने के तरीके = 60C5
∴ n(S) = 60C5
20 नीली गोलियाँ हैं इनमें से 5 गोलियाँ चुनने के तरीके = 20C5
5 नीली गोलियाँ निकालने की प्रायिकता

प्रश्न 2.
ताश के 52 पत्तों की एक अच्छी तरह फेंटी गई गड्डी से 4 पत्ते निकाले जाते हैं। इस बात की क्या प्रायिकता है कि निकाले गए पत्तों में 3 ईंट और एक हुकुम का पत्ता है ?
हल:

प्रश्न 3.
एक पासे के दो फलकों में से प्रत्येक पर संख्या 1 अंकित है। तीन फलकों में प्रत्येक पर संख्या 2 अंकित है और एक फलक पर संख्या 3 अंकित है। यदि पासा एक बार फेंका जाता है, तो निम्नलिखित ज्ञात कीजिए :
(i) P(2)
(ii) P(i या 3)
(iii) P(3 – नहीं)
हल:

(iii) 6 फलकों में 3 केवल एक फलक पर है।
अतः 3 प्राप्त न करने के तरीके = 6 – 1 = 5
∴ P(3 – नहीं) = 5/6.

प्रश्न 4.
एक लाटरी में 10000 टिकट बेचे गए जिनमें दस समान इनाम दिए जाने हैं। कोई भी इनाम न मिलने की प्रायिकता क्या है यदि आप
(a) एक टिकट खरीदते हैं
(b) दो टिकट खरीदते हैं
(c) 10 टिकट खरीदते हैं ?
हल:
टिकटों की संख्या जिन पर इनाम नहीं है
= 10000 – 10 = 9990
∵ कुल टिकटों की संख्या = 10000
(a) एक टिकट जिससे कोई इनाम नहीं मिलेगा ऐसे कुल तरीके
= 9990C1 = 9990
जबकि कुल संभावी परिणाम = 10,000
एक टिकट के साथ इनाम न मिलने की प्रायिकता

(ii) बिना इनाम वाले 9990 में से 2 टिकट मिलने के तरीके
= 9990C2
कुल 10000 टिकट हैं। उनमें से 2 टिकट पाने के तरीके
= 10000C2
.

(iii) इसी प्रकार 9990 में बिना इनाम वाले 10 टिकट को पाने के तरीके
= 9990C10
10000 में से 10 टिकट पाने के तरीके = 10000C10
अतः 10 टिकट के साथ इनाम न मिलने की प्रायिकता

प्रश्न 5.
100 विद्यार्थियों में से 40 और 60 विद्यार्थियों के दो वर्ग बनाए गए हैं। यदि आप और आपकाएक मित्र 100 विद्यार्थियों में हैं तो प्रायिकता क्या है कि
(a) आप दोनों एक ही वर्ग में हों।
(b) आप दोनों अलग-अलग वर्गों में हों।
हल:
माना दो वर्ग A और B हैं जिनमें क्रमशः 40 और 60 विद्यार्थी हैं।
(i) मान लीजिए दोनों विद्यार्थी वर्ग A में आते हैं।
∴ 98 विद्यार्थियों में से 38 विद्यार्थी चुने जाते हैं।
98 विद्यार्थियों में से 38 विद्यार्थी चुनने के तरीके = 98C38

दोनों विद्यार्थी (वह और उसका मित्र) एक ही वर्ग A में प्रवेश करने की प्रायिकता

(ii) यदि दोनों विद्यार्थी वर्ग B में प्रवेश करते हैं। तब 98 विद्यार्थियों में से 58 विद्यार्थी चुनने के तरीके = 98C58

अतः यदि वे विद्यार्थी वर्ग B में प्रवेश पाते हैं तो उसकी प्रायिकता


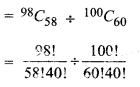
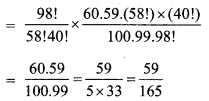
दोनों विद्यार्थी वर्ग A या वर्ग B में प्रवेश पाते हैं तो उसकी प्रायिकता

(b) दोनों विद्यार्थियों के विभिन्न वर्गों में प्रवेश पाने की प्रायिकता
.

प्रश्न 6.
तीन व्यक्तियों के लिए तीन पत्र लिखवाए गए हैं और प्रत्येक के लिए पता लिखा एक लिफाफा है। पत्रों को लिफाफों में यादृच्छया इस प्रकार डाला गया कि प्रत्येक लिफाफे में एक ही पत्र है। प्रायिकता ज्ञात कीजिए कि कम से कम एक पत्र अपने सही लिफाफे में डाला गया है।
हल:
मान लीजिए लिफाफों को A, B, C और संगत पत्रों को क्रमशः a, b, c से निरूपित किया गया है।
(i) एक पत्र उसके संगत लिफाफे में और दूसरे दो गलत लिफाफे में रखने के तरीके
(Aa, Bc, Cb), (Ac, Bb, Ca), (Ab, Ba, Cc)

(ii) यदि दो पत्र संगत (ठीक) लिफाफों में रखे गए हैं तो तीसरा भी संगत (ठीक) लिफाफे में होगा।

(iii) तीनों पत्र उनके संगत (ठीक) लिफाफों में रखे जाए (Aa, Bb, Cc) एक तरीका है।
पत्र कम से कम एक संगत लिफाफे में रखे जाने के तरीके
3 + 1 = 4
तीन पत्रों को तीन लिफाफा में रखने के कुल तरीके = 3! = 6
∴ कम से कम एक पत्र संगत लिफाफे में रखे जाने की प्रायिकता
= 4/6=2/3.

प्रश्न 7.
A और B दो घटनाएँ इस प्रकार हैं कि P(A) = 0.54, P(B) = 0.69 और P(A ∩ B) = 0.35, ज्ञात कीजिए:
(i) P(A ∪ B)
(ii) P(A’ ∩ B)
(iii) P(A ∩ B’)
(iv) P(B ∩ A’)
हल:
P(A) = 0.54, P(B) = 0.69, P(A ∩ B) = 0.35
P(A ∪ B) = P(A) + P(B) – (A ∩ B)
= 0.54 + 0.69 – 0.35 = 0.88

(ii)P(A’ ∩ B’) = P[(A ∪ B)’] = 1 – P(A ∪ B)
= 1 – 0.88 = 0.12.

(iii) P(A ∩ B’) = P(A) – P(A ∩ B)
= 0.54 – 0.35 = 0.19.

(iv) P(B ∩ A’) = P(B) – P(B ∩ A)
= 0.69 – 0.35 = 0.34.

प्रश्न 8.
एक संस्था के कर्मचारियों में से 5 कर्मचारियों का चयन प्रबन्ध समिति के लिए किया गया है। पाँच कर्मचारियों का ब्यौरा निम्नलिखित है :

इस समूह से प्रवक्ता पद के लिए यादृच्छया एक व्यक्ति का चयन किया गया। प्रवक्ता के पुरुष या 35 वर्ष से अधिक आयु का होने की प्रायिकता क्या है ?
हल:
माना A पुरुष के चयन और B व्यक्ति की आयु 35 वर्ष से अधिक को दर्शाते हैं।
पुरुषों की कुल संख्या = 3
35 वर्ष से अधिक आयु के कुल लोग = 2
35 वर्ष से अधिक आयु का पुरुष 1 है।

प्रश्न 9.
यदि 0, 1, 3, 5 और 7 अंकों द्वारा 5000 से बड़ी चार अंकों की संख्या का यादृच्छया निर्माण किया गया हो तो पाँच से भाज्य संख्या के निर्माण की क्या प्रायिकता है जब :
(i) अंकों की पुनरावृत्ति नहीं की जाए ?
(ii) अंकों की पुनरावृत्ति की जाए ?
हल:
(i) जब अंकों की पुनरावृत्ति नहीं होती।
मान लीजिए अंकों के स्थानों को I, II, III, IV से निरूपित किया गया हैं।
5000 से बड़ी संख्या बनाने के लिए स्थान I पर 5 या 7 रखना होगा अर्थात स्थान I को भरने के तरीके = 2
अब 5 अंक शेष रह जाते हैं।
स्थान II, III और IV को 4, 3 व 2 तरीकों से भर सकते हैं।
∴ 5000 से बड़ी संख्याएँ = 4 x 4 x 3 x 2 = 48 = n(S)
5 से भाज्य संख्याएँ वे हैं जब इकाई (स्थान IV) पर 0 या 5 हो। 5 को स्थान I पर तथा 0 को स्थान IV पर रखने के बाद 3 अंक बचते हैं। स्थान II और III, को 2 x 3 = 6 तरीकों से भरा जा सकता है।
इस प्रकार स्थान I पर जब 5 हो और IV पर 0 हो तो 6 संख्याएँ बनती हैं।
जब स्थान I पर 7 और स्थान IV पर 5 हो तो भी 6 संख्याएँ बनेंगी।
∴ 5000 से बड़ी और 5 से भाज्य संख्याएँ
= 6 + 6 + 6 = 18
अत: 5000 से बड़ी और 5 से भाज्य संख्याओं के बनने की प्रायिकता
= 18/24=3/4

(ii) जब पुनरावृत्ति की जा सकती है।
स्थान [ पर 5 या 7 रख सकते है जिससे संख्या 5000 से बड़ी बन सके।
∴ स्थान I को 2 तरीकों से भर सकते हैं।
क्योंकि पुनरावृत्ति की अनुमति है तो प्रत्येक स्थान II, III, IV को 5 तरीकों से भर सकते हैं।
चारों स्थानों को भरने के तरीके या 5000 से बड़ी संख्याएँ
= 2 × 5 × 5 × 5 = 250 = n(S)
संख्या यदि 5 से भाज्य है तो इकाई (IV) स्थान पर 0 या 5 रखना होगा।
इसलिए इकाई के स्थान को 2 तरीकों से भर सकते हैं।
बीच के स्थान II और III को 5 × 5 तरीकों से भर सकते हैं।
इस प्रकार 5000 से बड़ी और 5 से भाज्य संख्याएँ = 2 × 5 × 5 × 2 = 100
5000 से बड़ी और 5 से भाज्य बनाने वाली संख्याओं की प्रायिकता
= 100/250=2/5.

प्रश्न 10.
किसी अटैची के ताले में चार चक्र लगे हैं। जिनमें प्रत्येक पर 0 से 9 तक 10 अंक अंकित हैं। ताला चार अंकों के एक विशेष क्रम (अंकों की पुनरावृत्ति नहीं) द्वारा ही खुलता है। इस बात की क्या प्रायिकता है कि कोई व्यक्ति अटैची खोलने के लिए सही क्रम का पता लगा ले।
हल:
प्रथम स्थान पर कोई अंक 10 तरीकों से ही लाया जा सकता है। यहाँ 0, 1, 2, …. 9 में से कोई भी अंक ‘हो सकता है।
दूसरे, तीसरे व चौथे स्थान को 9 × 8 × 7 तरीकों से भरा जा सकता है।
इस प्रकार चार अंकों की संख्या (जबकि पुनरावृत्ति नहीं की गई है) बनने के तरीके = 10 × 9 × 8 × 7 = 5040
ताले को खोलने के लिए सही संख्या केवल एक ही है।
∴ अटैची को खोलने का सही क्रम ज्ञात करने की प्रायिकता = 1/5040.