Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.3
प्रश्न 1.
निम्न समीकरणों को हल कीजिए और अपने उत्तर की जाँच कीजिए –
1. 3x = 2x + 18
2. 5t – 3 = 3t – 5
3. 5x + 9 = 5 + 3x
4. 4z + 3 = 6 + 2z
5. 2x – 1 = 14 – x
6. 8x + 4 = 3(x – 1) + 7
7. x = (x + 10)
8. + 1 = +3
9. 2y + = – y
10. 3m = 5m –
हल:
1. 3x = 2x + 18
⇒ 3x – 2x = 18
(2x को बायीं ओर पक्षान्तर करने पर)
⇒ x = 18
जाँच: समीकरण में x = 18 रखने पर,
बायाँ पक्ष = 3x = 3 x 18 = 54
दायाँ पक्ष = 2x + 18 = 2 x 18 + 18
= 36 + 18 = 24
अतः x = 18 के लिए, बायाँ पक्ष = दायाँ पक्ष।
2. 2t – 3 = 3t – 5 – 3 को दायीं ओर तथा
-3 को बायीं ओर पक्षान्तर करने पर,
∴ 5t – 3t = – 5 + 3
2t = – 2
दोनों ओर 2 से भाग करने पर,
या t = – 1
जाँच: समीकरण में t = – 1 रखने पर,
बायाँ पक्ष = 5t – 3 = 5(-1) – 3 = – 5 – 3 = – 8
दायाँ पक्ष = 3t – 5 = 3(-1) – 5 = – 3 – 5 = – 8
अतः t = – 1 के लिए, बायाँ पक्ष = दायाँ पक्ष
3. 5x + 9 = 5 + 3x
या 5x – 3x = 5 – 9
(3x को बायीं ओर 9 को दायीं ओर पक्षान्तर करने पर)
या 2x = – 4
या =
(दोनों पक्षों को 2 से भाग करने पर)
या x = – 2
जाँच: समीकरण में x = – 2 रखने पर,
बायाँ पक्ष = 5x + 9= 5 (-2) +9 = – 10 + 9 = – 1
दायाँ पक्ष = 5 + 3x = 5 + 3 x (-2)= 5 – 6 = – 1
अतः x = – 2 के लिए, बायाँ पक्ष = दायाँ पक्ष।
4. 4z + 3 = 6 + 2z
या 4z – 2z = 6 – 3
(3 को दायीं ओर और 6 को बायीं ओर पक्षान्तर करने पर)
या 2z = 3
या =
(दोनों पक्षों को 2 से भाग करने पर)
या x =
जाँच: समीकरण में z = 3/2 रखने पर,
बायाँ पक्ष = 4z + 3 = 4 x + 3 = 6 + 3 = 9
दायाँ पक्ष = 6 + 2x = 6 + 2 x = 6 + 3 = 9.
अतः z = 3/2 के लिए, बायाँ पक्ष = दायाँ पक्ष।
5. 2x – 1 = 14 – x
2x + x = 14+1
(-1 को दायीं ओर तथा –x को बायीं ओर पक्षान्तर करने पर)
या 3x = 15
या
(दोनों पक्षों को 3 से भाग करने पर)
या x = 5
जाँच: समीकरण में x = 5 रखने पर,
बायाँ पक्ष = 2x – 1 = 2 x 5 – 1 = 10 – 1 = 9
दायाँ पक्ष = 14 – x = 14 – 5 = 9
अतः x = 5 के लिए, बायाँ पक्ष = दायाँ पक्ष।
6. 8x+ 4 = 3(x – 1) + 7
या 8x + 4 = 3x – 3 + 7
या 8x + 4 = 3x + 4
या 8x – 3x = 4 – 4
(3x को बायीं ओर और 4 को दायीं ओर पक्षान्तर करने पर)
या 5x = 0 ⇒ =
(दोनों ओर 5 से भाग करने पर)
या x = 0
जाँच: समीकरण में x = 0 रखने पर,
बायाँ पक्ष = 8x + 4 = 0 = 8 x 0 + 4 = 0 + 4 =4
दायाँ पक्ष = 3(x – 1) + 7 = 3(0 – 1) + 7 = – 3 + 7 = 4
अतः x = 0 के लिए, बायाँ पक्ष = दायाँ पक्ष।
7. x = (x + 10)
या 5x = 4(x + 10)
(दोनों ओर 5 से गुणा करने पर)
या 5x = 4x + 40
या 5x – 4x = 40
(4x का पक्षान्तर करने पर)
या x = 40
जाँच: समीकरण में x = 40 रखने पर,
बायाँ पक्ष = x = 40
दायाँ पक्ष = (x + 10) = (40 + 10) = = 40
अतः x = 40 के लिए, बायाँ पक्ष = दायाँ पक्ष।
8. + 1 = + 3
दोनों पक्षों को 15 से गुणा करने पर,
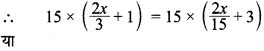
या 10x + 15 = 7x + 45
या 10x – 7x = 45 – 15
(7x तथा 15 को पक्षान्तर करने पर)
या 3x = 30
या =
(दोनों ओर 3 से भाग करने पर)
या x = 10
जाँच: समीकरण में x = 10 रखने पर,
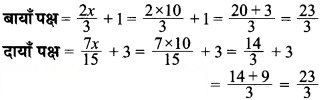
अत: x = 10 के लिए, बायाँ पक्ष = दायाँ पक्ष।
9. 2y + 53 = – y
या 2y + y = –
( तथा – y को पक्षान्तर करने पर)

(दोनों ओर 3 से भाग करने पर)
या y =
जाँच: समीकरण में y = रखने पर
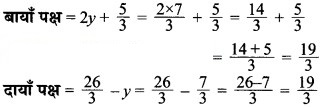
अतः y = के लिए, बायाँ पक्ष = दायाँ पक्ष।


अतः m = के लिए, बायाँ पक्ष = दायाँ पक्ष।