Chapter 2 एक चर वाले रैखिक समीकरण Ex 2.5
प्रश्न 1.
निम्न रैखिक समीकरणों को हल कीजिए –

हल:
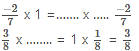
3. x + 7 – = –
2, 3 व 6 का ल. स. = 12
दोनों पक्षों को 12 से गुणा करने पर,
12 x (x + 7 – ) = 12 x ( – )
या 12x + 84 – 32x = 34 – 30x
या 12x – 32x + 30x = 34 – 84
या 10x = – 50
x =
x = – 5
4. =
5 (x – 5) = 3 (x – 3)
या 15x – 25 = 3x – 9
या 5x – 3x = – 9 + 25
या 2x = 16
या x =
या x = 8
5. – = – t
ल. स. = 3 x 4 = 12
दोनों पक्षों को 12 से गुणा करने पर,
12 x () = 12 x ( – t)
या 9t – 6 – 81 – 12 = 8 – 12t
या 9t – 8t + 12t = 8+ 6 + 12
या 13t = 26
या t = = 2
6. m – = 1 –
2 व 3 का ल. स. = 2 x 3 = 6
दोनों पक्षों को 6 से गुणा करने पर
6 (m – ) = 6 (1 – )
या 6m – 3 (m – 1) = 6 – 2 (m – 2)
या 6m – 3m + 3 = 6 – 2m + 4
या 6m – 3m + 2m = 6 + 4 – 3
या 5m = 7
या m =
प्रश्न 2.
निम्न समीकरणों को सरल रूप में बदलते हुए हल कीजिए –
7. 3 (t – 3) = 5 (2t + 1)
8. 15 (y – 4) – 2 (7 – 9) + 5 (v + 6) = 0
9. 3 (5z – 7) – 2 (9z – 11)= 4 (8z – 13) – 17
10. 0.25 (4f – 3) = 0.05 (10f – 9)
हल:
7. 3 (t – 3) = 5 (2t + 1)
3t – 9 = 10t + 5
या 3t – 10t = 5 + 9
या 7t = -14
या t= = – 2
8. 15 (y – 4) – 2 (y – 9) + 5 (y + 6) = 0
15y – 60 – 2y + 18 + 5y + 30 = 0
या 15y – 2y + 5y = 60 – 18 – 30
या 18y = 12
या y = =
9. 3 (5z – 7) – 2 (9z – 11)= 4 (8z – 13) – 17
15z – 21 – 18z + 22 = 32z – 52 – 17
या 15z – 18z – 32z = – 52 – 7 + 21 – 22
या – 35z = – 70
या z =
z = 2
10. 0.25 (4f – 3) = 0.05 (10f – 9)
f – 0.75 = 0.5f – 0.45
या f – 0.5f = – 0.45 + 0.75
या 0.5f = 0.30
या f=
या f= 0.6